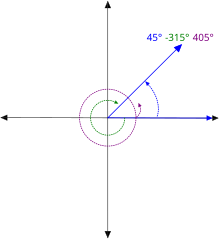
45度的3个同界角 在几何学 中,同界角 (英语:Coterminal angles )是指两个有向角 (有标示起始边与终边的角)有着各自的角度量值(其量值可能相等),且共用同一对起始边与终边,即共享相同始边和终边的角度,但拥有不同的旋转 量,就称为同界角 [ 1] 三角函数 值,因此三角函数具有周期性 。每个角皆有无限多 个同界角 ,其量值可以为负 ,但必须是一个实数 。
正转 和逆转 都可以得到相同的角 ,但他们拥有不同的旋转量,图中为45度和─ 315度每个同界角皆差360度 ,换句话说,每360度就会出现一个同界角[ 2] 向量 内积 与外积 皆有相同的值。此外,任何角都可以找到最小正同界角 和最大负同界角 。
同界角可以如下定义:
若有两个角有相同的始边 与终边,则两个角互为同界角
若两角相差360度的整数 倍则两个角互为同界角 同界角存在关系式:
θ
1
−
θ
2
=
360
∘
k
,
k
∈
Z
{\displaystyle \theta _{1}-\theta _{2}=360^{\circ }k,\,k\in \mathbb {Z} }
亦可写为:
θ
1
−
θ
2
=
2
k
π
,
k
∈
Z
{\displaystyle \theta _{1}-\theta _{2}=2k\pi ,\,k\in \mathbb {Z} }
或:
sin
θ
1
−
sin
θ
2
=
0
{\displaystyle \sin \theta _{1}-\sin \theta _{2}=0}
cos
θ
1
−
cos
θ
2
=
0
{\displaystyle \cos \theta _{1}-\cos \theta _{2}=0}
从三角函数 的周期 可以发现,每间隔
2
π
{\displaystyle 2\pi }
从反三角函数 图形得知反余弦 必得到最小正同界角 ,而反正弦 则有可能得到最小正同界角 或最大负同界角 从三角函数 的诱导公式 可以得知同界角的存在,下表指出,任何三角函数,只要位移为
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
θ
+
2
π
{\displaystyle \theta +2\pi }
移位
π
2
{\displaystyle {\frac {\pi }{2}}}
移位
π
{\displaystyle \pi }
tan
{\displaystyle \tan }
cot
{\displaystyle \cot }
移位
2
π
{\displaystyle 2\pi }
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
csc
{\displaystyle \csc }
sec
{\displaystyle \sec }
sin
(
θ
+
π
2
)
=
+
cos
θ
cos
(
θ
+
π
2
)
=
−
sin
θ
tan
(
θ
+
π
2
)
=
−
cot
θ
cot
(
θ
+
π
2
)
=
−
tan
θ
sec
(
θ
+
π
2
)
=
−
csc
θ
csc
(
θ
+
π
2
)
=
+
sec
θ
{\displaystyle {\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \\\sec(\theta +{\tfrac {\pi }{2}})&=-\csc \theta \\\csc(\theta +{\tfrac {\pi }{2}})&=+\sec \theta \end{aligned}}}
sin
(
θ
+
π
)
=
−
sin
θ
cos
(
θ
+
π
)
=
−
cos
θ
tan
(
θ
+
π
)
=
+
tan
θ
cot
(
θ
+
π
)
=
+
cot
θ
sec
(
θ
+
π
)
=
−
sec
θ
csc
(
θ
+
π
)
=
−
csc
θ
{\displaystyle {\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\cot(\theta +\pi )&=+\cot \theta \\\sec(\theta +\pi )&=-\sec \theta \\\csc(\theta +\pi )&=-\csc \theta \end{aligned}}}
sin
(
θ
+
2
π
)
=
+
sin
θ
cos
(
θ
+
2
π
)
=
+
cos
θ
tan
(
θ
+
2
π
)
=
+
tan
θ
cot
(
θ
+
2
π
)
=
+
cot
θ
sec
(
θ
+
2
π
)
=
+
sec
θ
csc
(
θ
+
2
π
)
=
+
csc
θ
{\displaystyle {\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\cot(\theta +2\pi )&=+\cot \theta \\\sec(\theta +2\pi )&=+\sec \theta \\\csc(\theta +2\pi )&=+\csc \theta \end{aligned}}}
另外,从简单的三角方程中,也可以找到同界角,例如:
考虑方程
cos
(
θ
)
=
k
,
θ
{\displaystyle \cos(\theta )=k\,,\,\theta }
arccos
(
k
)
{\displaystyle \arccos(k)}
最小正同界角 ,其余解皆与
arccos
(
k
)
{\displaystyle \arccos(k)}
arccos
(
k
)
{\displaystyle \arccos(k)}
但是有例外,如正切 和余切 ,由于其周期 不为360度,如正切函数的周期为180 度 (即
π
{\displaystyle \pi }
角的量与最小正同界角(黄)与最大负同界角(蓝)的关系 同界角通常有无穷多个,因此在计算一些角度或三角函数抑或是一些周期函数的解时,会取最接近零的同界角。这类同界角又可以再分成最小正同界角与最大负同界角。其中,最小正同界角恒为正, 通常解某些具周期性的方程的主值时,是使用最小正同界角。最小正同界角
2
π
{\displaystyle 2\pi }
2
π
{\displaystyle 2\pi }
2
π
{\displaystyle 2\pi }
最大负同界角恒为负,在
−
2
π
{\displaystyle -2\pi }
^ Neal, Karla V.; R. David Gustafson, Jeffrey D. Hughes. Coterminal angles . Precalculus, 1st ed.. Cengage Learning. : 第412页. ISBN 1133712673存档 于2019-10-18). ^ Slavin, Steve; Ginny Crisonino. Circle . Wiley Self-Teaching Guides第 155 卷. John Wiley & Sons. 2004-10-28: 第90页. ISBN 0471680192存档 于2019-11-06).