纳皮尔的骨头
此条目需要扩充。 (2007年9月26日) |
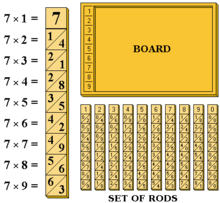
纳皮尔的骨头(英语:Napier's bones)是苏格兰数学家约翰纳皮尔发明的一种用来计算乘法与除法,类似算盘的工具。由一个底座及九根圆柱(方柱)组成,可以把乘法运算转为加法,也可以把除法运算转为减法。更为进阶的用法也可以开平方根
纳皮尔的骨头在清初传入中国,数学家梅文鼎在《梅氏丛书辑要》中最先介绍纳皮尔的骨头,梅氏称之为“筹算”。后来戴震著作《策算》也叙述了这种算法[1]。

简介
[编辑]底座左边的数字由上而下是1-9。先将之称为n。
每根圆柱又分为十格,下面九格有自左下而右上的斜线。最上面的格子写著1-9的数字,姑且称为k,代表著这根柱子的编号。编号下面的数字则是由k乘上横排相对应的n得到的,十位数摆左上角,个位数摆右下角。
乘法运算
[编辑]举例说明如何用纳皮尔的骨头进行乘法运算。
46785399乘以7
1.把编号4,6, 7,8, 5,3, 9,9的圆柱依序放入底座。
2.如下图将结果相加即得到乘积(记得要进位)。
46785399乘以96431
1.把编号4,6, 7,8, 5,3, 9,9的圆柱依序放入底座。
2.将46785399乘以9,6, 4,3, 1分别用上述方法一条一条算出来。
3.接著用直式加法把数字加起来。
除法运算
[编辑]同样举例说明。
46785399除以96431
1.把除数(96431)编号的柱子摆入底座。
2.如下图所示把96431乘以1-9的结果写出来。
3. 46785399从左边六位开始看,下面写上小于467853但最大的96431k。
4.用467853去减96431k(此例中k=4),得到的数字写下面。
5.把上面的数字(9)移下来,如同长除法般重复进行此动作。
6.最后得到一个比96431还小的数,为馀数。
7.如有需要,可以一直进行除法工作以得到小数点位数。
开平方根
[编辑]用来开平方根的纳皮尔的骨头会用到第十根柱子,上有三个直排。第一排上有数字1-9的平方,第二排是数字2,4, ...,18,第三排则是1-9。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0/1 | 0/2 | 0/3 | 0/4 | 0/5 | 0/6 | 0/7 | 0/8 | 0/9 | 0/1 2 1 |
| 2 | 0/2 | 0/4 | 0/6 | 0/8 | 1/0 | 1/2 | 1/4 | 1/6 | 1/8 | 0/4 4 2 |
| 3 | 0/3 | 0/6 | 0/9 | 1/2 | 1/5 | 1/8 | 2/1 | 2/4 | 2/7 | 0/9 6 3 |
| 4 | 0/4 | 0/8 | 1/2 | 1/6 | 2/0 | 2/4 | 2/8 | 3/2 | 3/6 | 1/6 8 4 |
| 5 | 0/5 | 1/0 | 1/5 | 2/0 | 2/5 | 3/0 | 3/5 | 4/0 | 4/5 | 2/5 10 5 |
| 6 | 0/6 | 1/2 | 1/8 | 2/4 | 3/0 | 3/6 | 4/2 | 4/8 | 5/4 | 3/6 12 6 |
| 7 | 0/7 | 1/4 | 2/1 | 2/8 | 3/5 | 4/2 | 4/9 | 5/6 | 6/3 | 4/9 14 7 |
| 8 | 0/8 | 1/6 | 2/4 | 3/2 | 4/0 | 4/8 | 5/6 | 6/4 | 7/2 | 6/4 16 8 |
| 9 | 0/9 | 1/8 | 2/7 | 3/6 | 4/5 | 5/4 | 6/3 | 7/2 | 8/1 | 8/1 18 9 |
求出46785399的平方根
1.把46785399分为两位两位一组,46 78 53 99。(如果奇数位数,如83559,写成8 35 59)
2.从最左边那组,46,开始。找出比这数最小的完全平方数,是在第六横排上的36。
3.因为是从第六横排上挑出来的,所以答案的第一位是6。
4.找到第十根柱子上的第六横排第二直排,12,然后把1跟2的柱子放在底座上。
5.用46减去36得到10,然后把上面下一组的78移到10的右边。
|
_____________
√46 78 53 99 = 6
36
--
10 78
|
7.找出比1078还要小但最大的数,在此第八横排的1024是最大的:
0/8 1/6 6/4 → 1024
8. 8为答案的下一位数,写在6旁边,然后把1078减去1024得到54。
|
_____________
√46 78 53 99 = 68
36
--
10 78
10 24
-----
54
|
9.把之前的12乘上10,再加上第十根柱子第八横排第二直排的数,16,得136。
10.重复上述步骤可得到结果:
|
_____________
√46 78 53 99 = 68
36
--
10 78
10 24
-----
54 53
|
11.再次找到比5453还要小但最大的数,为4089。5453减去4089为1364,并把3写在68的旁边。
|
_____________
√46 78 53 99 = 683
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64
|
12.把3乘2的结果加上之前136的十倍,得到1366。把1,3, 6,6的版子摆入底座。
13.再度重复上述步骤。现在比最底下的数小的数是第九横排的123021。
|
_____________
√46 78 53 99 = 6839
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78
|
14.再把9加到答案当中,得到整数答案6839。
我们把题目给的数46785399用完了,但是底下还有馀数13478。这意味著6839只是答案的整数部分,的实际值应当比6839大,比6840小。如果有需要继续做下去以得到小数部分的话,下一组的两个数字就要用00:
|
_____________
√46 78 53 99 = 6839.
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78 00
|
这些步骤可以一直重复使得到的答案无限逼近正解。
最后,如果要求平方根的数是小数的话,将数字分组的时候整数部分跟小数部分要分开分组;整数部分如常,小数部分则是方向相反。
例如数字54782.917的分组情况为:
5 47 82 . 91 7
接著便可开平方。




