质数间隙

质数间隙的频率分布。

质数间隙是指两个相邻质数间的差值。第n个质数间隙，标记为g_n 或g(p_n)，指第n个质数和第n+1个质数间的差值，即

$g_{n}=p_{n+1}-p_{n}.\$

可知，g₁ = 1、g₂ = g₃ = 2，以及g₄ = 4。由质数间隙组成的数列(g_n) 已被广泛地研究，但仍有许多问题及猜想尚未获得解答。

前30个质数间隙为：

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14 A001223.

由g_n 的定义，可得g_n 及第n+1个质数的关系式如下：

$p_{n+1}=2+\sum _{i=1}^{n}g_{i}$ .

张益唐在2013年证明：存在有无限多对质数，其间隙小于七千万；之后于同年十一月，詹姆斯·梅纳德用精进版的GPY筛法将间隙改进至600，而由陶哲轩发起的Polymath计划将这数字降到246。

简单观察

第1个、最小，且唯一为奇数的质数间隙为1，是在“唯一一个偶质数2”与“第一个奇质数3”之间的质数间隙。剩下的其他质数间隙均为偶数。在3个相邻的质数间的1对质数间隙均为质数，只有在质数3、5及7之间的g₂ 及g₃ 一种而已。

对任一质数P，可定义一质数乘积P#，为所有小于等于P的质数之乘积。若Q为P之后的质数，则数列

$P\#+2,P\#+3,\ldots ,P\#+(Q-1)$

为由相邻的Q-2个合数组成的数列，亦即存在一个长度至少为Q-1的质数间隙。因此，质数间的间隙可以是任意大的，亦即对任一质数P，总存在一个整数n，使得g_n ≥ P。（可选定n，使得p_n为小于P# + 2 的最大质数）另外，依据《质数定理》，质数的密度会随着数值增大而趋近于0，亦可知存在任意大的质数间隙。实际上，依《质数定理》，P# 的值约略为 exp(P)的大小，且于 exp(P)附近，相邻质数的“平均”间隙为 P。

实际上，质数间隙为P 的数可能会远小于P#。例如，由71个相邻合数组成的最小数列介于31398至31468间，但71#有“27个数位”，其完整的十进制表示为 557940830126698960967415390。

孪生质数猜想主张存在无限多个整数n，使得 g_n = 2。

数值结果

一般将${\textstyle {\frac {g_{n}}{\ln(p_{n})}}}$给称作$g_{n}$的努力值（merit）。非正式地，一个质数间隙$g_{n}$的努力值可视为一个质数间隙和$p_{n}$附近的平均间隙大小之间的比值。

目前最大的、和一个可能质数相关的间隙，其大小为16,045,848，和一个385,713位的可能质数有关，而其努力值$M=18.067$。这数由Andreas Höglund在2024年3月发现。而最大的和确认的质数相关的质数间隙，其大小为1,113,106，努力值为25.90，和一个18,662位的质数有关，发现者是P. Cami, M. Jansen和J. K. Andersen。

截至2022年9月 (2022-09)为止，已知最大的及第一个超过40的努力值由Gapcoin网络所发现，其数值为41.93878373，和一个87位的质数有关​，这个质数和下一个质数之间的间隙的大小为8350。

截至2020年10月年 (2020年10月-Missing required parameter 1=month!)为止最大已知的努力值

努力值	$g_{n}$	位数	$p_{n}$	日期	发现者
41.938784	08350	0087	见上	2017	Gapcoin
39.620154	15900	0175	3483347771 × 409#/0030 − 7016	2017	Dana Jacobsen
38.066960	18306	0209	0650094367 × 491#/2310 − 8936	2017	Dana Jacobsen
38.047893	35308	0404	0100054841 × 953#/0210 − 9670	2020	Seth Troisi
37.824126	08382	0097	0512950801 × 229#/5610 − 4138	2018	Dana Jacobsen

Cramér–Shanks–Granville比值指的是$g_{n}/(\ln {p_{n}})^{2}$这个比值。若不计2、3及7的异常高的值的话，那目这比值已知最大的数值是1693182318746371的0.9206386。其他已知的数值可见A111943。

若对于所有的$m<n$而言，都有$g_{m}<g_{n}$，则称$g_{n}$是最大间隙。截至2024年10月 (2024-10)，已知最大的最大间隙其值是1676，发现者为Brian Kehrig。这是第83个最大间隙，出现于20733746510561442863这质数之后。

其他已知的最大间隙可见于A005250，而与之相关的质数$p_{n}$可见于A002386，相关的n则可见于A005669。目前猜想，不大于第n个质数的最大间隙组成的数列大约有$2\ln n$ 项。

83个已知的最大质数间隙

从1至28 # gn pn 1 1 2 2 2 3 3 4 7 4 6 23 5 8 89 6 14 113 7 18 523 8 20 887 9 22 1,129 10 34 1,327 11 36 9,551 12 44 15,683 13 52 19,609 14 72 31,397 15 86 155,921 16 96 360,653 17 112 370,261 18 114 492,113 19 118 1,349,533 20 132 1,357,201 21 148 2,010,733 22 154 4,652,353 23 180 17,051,707 24 210 20,831,323 25 220 47,326,693 26 222 122,164,747 27 234 189,695,659 28 248 191,912,783

从29至56 # gn pn 29 250 387,096,133 30 282 436,273,009 31 288 1,294,268,491 32 292 1,453,168,141 33 320 2,300,942,549 34 336 3,842,610,773 35 354 4,302,407,359 36 382 10,726,904,659 37 384 20,678,048,297 38 394 22,367,084,959 39 456 25,056,082,087 40 464 42,652,618,343 41 468 127,976,334,671 42 474 182,226,896,239 43 486 241,160,624,143 44 490 297,501,075,799 45 500 303,371,455,241 46 514 304,599,508,537 47 516 416,608,695,821 48 532 461,690,510,011 49 534 614,487,453,523 50 540 738,832,927,927 51 582 1,346,294,310,749 52 588 1,408,695,493,609 53 602 1,968,188,556,461 54 652 2,614,941,710,599 55 674 7,177,162,611,713 56 716 13,829,048,559,701

从57至83 # gn pn 57 766 19,581,334,192,423 58 778 42,842,283,925,351 59 804 90,874,329,411,493 60 806 171,231,342,420,521 61 906 218,209,405,436,543 62 916 1,189,459,969,825,483 63 924 1,686,994,940,955,803 64 1,132 1,693,182,318,746,371 65 1,184 43,841,547,845,541,059 66 1,198 55,350,776,431,903,243 67 1,220 80,873,624,627,234,849 68 1,224 203,986,478,517,455,989 69 1,248 218,034,721,194,214,273 70 1,272 305,405,826,521,087,869 71 1,328 352,521,223,451,364,323 72 1,356 401,429,925,999,153,707 73 1,370 418,032,645,936,712,127 74 1,442 804,212,830,686,677,669 75 1,476 1,425,172,824,437,699,411 76 1,488 5,733,241,593,241,196,731 77 1,510 6,787,988,999,657,777,797 78 1,526 15,570,628,755,536,096,243 79 1,530 17,678,654,157,568,189,057 80 1,550 18,361,375,334,787,046,697 81 1,552 18,470,057,946,260,698,231 82 1,572 18,571,673,432,051,830,099 83 1,676 20,733,746,510,561,442,863

更多结果

上界

1852年得到证明的伯特兰-切比雪夫定理显示，在$k$跟$2k$之间，总有一个质数，特别地，$p_{n+1}<2p_{n}$，因此$g_{n}<p_{n}$。

1896年得证的质数定理显示说对足够大的质数而言，一个质数$p$和下一个质数之间的间隙，会非病态地接近$\ln {p}$，也就是$p$的自然对数，而实际的质数间隙可能远大或远小于此；

然而我们可以从质数定理推出说质数间隙跟质数的比会变得任意小，如下式所示：

$\lim _{n\to \infty }{\frac {g_{n}}{p_{n}}}=0.$

以极限的定义来说，对于任意的$\epsilon >0$，存在一个数$N$，使得对于所有的$n>N$而言，有

$g_{n}<p_{n}\epsilon$

基多·何海赛尔在1930年首次证明了以下的非线性关系，他证明了说，存在一个常数$\theta <1$，使得下式成立：

$\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}{\text{ as }}x\to \infty ,$

由此他证明了，对于足够大的n，有以下关系：

$g_{n}<p_{n}^{\theta }$

何海赛尔证明说$\theta$小于等于32999/33000；之后海尔布龙将之给改进到249/250；而胡打科夫证明了说对于任意的$0<\varepsilon$而言，$\theta ={\frac {3}{4}}+\varepsilon$。

一个主要的改进由英厄姆做出，他证明了说存在一个正的常数$c$，使得下式成立：

if $\zeta (1/2+it)=O(t^{c})$ then $\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}$ for any $\theta >(1+4c)/(2+4c).$

此处，$O$代表大O符号，$\zeta$代表黎曼ζ函数，而$\pi$是质数计数函数。由于${\frac {1}{6}}<c$是可行的数之故，因此可知$\theta$可以是任何大于${\frac {5}{8}}$的数。

英厄姆结果的一个立即的推论是，在n足够大时，在$n^{3}$及$(n+1)^{3}$之间总有一个质数；而从林德勒夫猜想可推出，英厄姆的公式对于任意正数$c$都成立；然而这两者都不足以推出勒让德猜想，也就是在$n^{2}$及$(n+1)^{2}$之间总有一个质数这猜想。要证明这点，像是克拉梅尔猜想等更强的结果会是必要的。

赫胥黎在1972年证明说，$\theta ={\frac {7}{12}}=0.583\cdots$是可能的。

贝克、哈曼和平茨在2001年正明说$\theta \cdots$可以缩小到0.525。

上述的结果适用于“所有的”间隙，而人们对“最小的”间隙也感兴趣。孪生质数猜想说，有无限多的质数，其间隙为2。在2005年，Goldston、Pintz和Yildirim三氏证明了以下关系：

$\liminf _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=0$

两年后他们又将之改进如下： to

$\liminf _{n\to \infty }{\frac {g_{n}}{{\sqrt {\log p_{n}}}(\log \log p_{n})^{2}}}<\infty .$

2013年，张益唐证明了以下关系：

$\liminf _{n\to \infty }g_{n}<7\cdot 10^{7},$

这表示说，有无限多的质数间隙，其大小不超过七千万。之后Polymath计划的集体努力，在2013年7月20日，将张益唐界限给降到了4680。

在2013年11月，詹姆斯·梅纳德改进了GPY筛法，并以之将上界给降到600，并证明了说两个彼此间隔$m$个质数的质数，其间隙有上限。也就是说，对于任意的正整数$m$，总存在一个界限$\Delta _{m}$，使得对于无穷多的n而言，$p_{n+m}-p_{n}\leq \Delta _{m}$。利用梅纳德的想法，Polymath计划将上界给降到了246，并证明了说在假定埃利奥特–哈尔伯斯坦猜想和其推广的状况下，分别可将上界给降到12和6。

下界

1931年，埃里克·韦斯钦蒂乌斯（Erik Westzynthius）证明质数间隙成长速度快过对数，也就是说，

$\limsup _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=\infty .$

罗伯特·亚历山大·兰金在1938年改进了韦斯钦蒂乌斯和艾狄胥·帕尔的结果，证明了说存在一个常数$c>0$，使得以下不等式对无限多个n成立：

$g_{n}>{\frac {c\ \log n\ \log \log n\ \log \log \log \log n}{(\log \log \log n)^{2}}}$

之后他又证明了说上式对任何的$c<e^{\gamma }$都成立，其中$\gamma$是欧拉-马斯刻若尼常数。常数$c$的值在1997年改进至$c<2e^{\gamma }$。

艾狄胥·帕尔提供了10,000美元的奖金给任何能证明或否证上述的常数$c$可以任意大的人。这点在2014年由凯文·福特、本·格林、谢尔盖·科尼亚金和陶哲轩四人组以及詹姆斯·梅纳德分别独立证出。

之后这结果被上述五人改进成对无限多个n而言，以下不等式成立：

$g_{n}>{\frac {c\ \log n\ \log \log n\ \log \log \log \log n}{\log \log \log n}}$

做为向艾狄胥原始奖金精神的致意，陶哲轩提供了10,000美元的奖金给任何能证明或否证上述的常数$c$可以任意大的人。

目前也已知关于质数链的下界。

关于质数间隙的猜想

如上所言，目前已知最好的关于质数间隙的结果是对于足够大的n而言，$g_{n}<p_{n}^{0.525}$（因此诸如$5-3>3^{0.525}$或$29-23>23^{0.525}$这样的情况是不考虑的）但目前观察到的结果是，即使最大的间隙，也远小于此，也因此生出了一系列未证明的猜想。

首先，有猜想认为，对于上述何海赛尔的结果，有$\theta =0.5$。

勒让德猜想认为，在两个完全平方数之间，都总有一个质数，而这意味着说，$g_{n}=O({\sqrt {p_{n}}})$；安德里卡猜想则指出说：

$g_{n}<2{\sqrt {p_{n}}}+1$

奥珀曼猜想意味着更强的结果，就是对于任意足够大的n而言（或许对任何的$n>30$而言），总有以下关系：

$g_{n}<{\sqrt {p_{n}}}.$

上述的关系都未得证明，而哈拉尔德·克拉梅尔证明了说若黎曼猜想成立，那在用大O符号表述的状况下，质数间隙$g_{n}$会满足以下关系：

$g_{n}=O({\sqrt {p_{n}}}\log p_{n}),$

（实际上，如果允许任意大的指数的话，这结果只需要较弱的林德勒夫猜想）

质数间隙函数

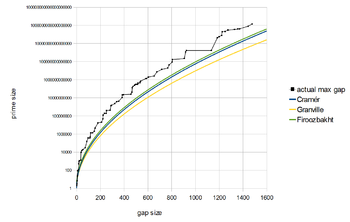
与此同时，克拉梅尔也猜想说质数间隙远小于此，而他的猜想即是克拉梅尔猜想，克拉梅尔猜想表示说：

$g_{n}=O\!\left((\log p_{n})^{2}\right)\!,$

也就是说，其成长率是一个小于任何指数$\theta >0$的多对数函数。

克拉梅尔猜想符合观察到的质数间隙，此外也有其他类似的猜想。菲鲁兹巴赫特猜想稍强于此，菲鲁兹巴赫特猜想认为，$p_{n}^{1/n}\!$是个对n的严格递减函数，也就是说，对于任意的$n\geq 1$而言，有以下关系：

$p_{n+1}^{1/(n+1)}\!<p_{n}^{1/n}$

若这猜想成立，就表示说对于任意的$n>9$而言，有$g_{n}<(\log p_{n})^{2}-\log p_{n}-1$从该猜想可推出强克拉梅尔猜想，而这与安德鲁·格兰维尔、平茨·亚诺什等人的猜测不一致。他们的猜测认为，对于$\varepsilon >0,$而言，有无限多质数间隙，使得$g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}>(1.1229-\varepsilon )(\log p_{n})^{2}$，其中$\gamma$是欧拉-马斯刻若尼常数。

波利尼亚克猜想表示说，对于任何的正偶数k，都总有无限多个质数间隙等于k。{{{1}}}的情况即孪生质数猜想。目前尚未对这猜想任何特定的k成立或不成立，但如上所言，由于张益唐以及随后的改进，目前已知这猜想对至少一个$k\leq 246$成立。

作为数论函数

表示第n个质数及其之后的质数间隙的$g_{n}$是数论函数的一个例子，在将之视为数论函数的状况下，一般都把质数间隙给记做$d_{n}$并称之为质数差函数。这函数非积性函数，也非加性函数。

另见

• Bonse不等式
• Interprime
• Gaussian moat
• 孪生质数

• 孪生质数猜想

参考资料

• Guy, Richard K. Unsolved problems in number theory 3rd. Springer-Verlag. 2004. ISBN 978-0-387-20860-2. Zbl 1058.11001. 

外部链接

• Thomas R. Nicely, Some Results of Computational Research in Prime Numbers -- Computational Number Theory. This reference web site includes a list of all first known occurrence prime gaps.
• 埃里克·韦斯坦因. Prime Difference Function. MathWorld. 
• Prime Difference Function. PlanetMath. 
• Armin Shams, Re-extending Chebyshev's theorem about Bertrand's conjecture （页面存档备份，存于互联网档案馆）, does not involve an 'arbitrarily big' constant as some other reported results.
• Chris Caldwell, Gaps Between Primes （页面存档备份，存于互联网档案馆）; an elementary introduction
• www.primegaps.com （页面存档备份，存于互联网档案馆） A study of the gaps between consecutive prime numbers
• Andrew Granville, Primes in Intervals of Bounded Length （页面存档备份，存于互联网档案馆）; overview of the results obtained so far up to and including James Maynard's work of November 2013.