跳转到内容

星形二十面体列表

编辑链接
本页使用了标题或全文手工转换
维基百科，自由的百科全书
一种星形二十面体，其杜瓦记号计为De1

下表列出了一些可以用二十面体星状图表示的星形二十面体，其中有58种收录于哈罗德·斯科特·麦克唐纳·考克斯特的《五十九种二十面体》[1]、21种星形二十面体收录于《多面体模型》。构成这些星形二十面体的星形胞有12个，分别为a、b、c、d、e1、e2、f1、f1、f2、g1、g2和h。《五十九种二十面体》收录的多面体中有27种都出现歪斜的外观。它也包含特殊形状如大二十面体、复合的多面体、扭曲的形状，皆只收录一种。

第二种星形二十面体

[编辑]
更多信息：十复合正四面体 § 第二星形二十面体

在几何学，第二星状二十面体是一种非凸多面体，属于星形多面体，是哈罗德·斯科特·麦克唐纳·考克斯特的《五十九种二十面体》中收录的第二种第二种星形多面体。它可视为11个多面体的复合体，包括了十个四面体和中间一个大三角六边形二十面体。它可视为多面体的星状复合物，因此有时称做复合星状多面体。温尼尔的《多面体模型》有收录该多面体，其索引为W27。

第二星状二十面体是星形二十面体的第二个星形多面体，是从二十面体衍生的多面体。

表格

[编辑]

复合多面体

[编辑]

星形多面体有些可以拆成多个子多面体，换句话说，有些星形多面体是由数个其他多面体组合而成的，较容易理解的类比比如六角星、大卫之星，是由两个三角形嵌合在一起构成的。下表列出一些由若干多面体嵌合在一起构成的星形二十面体。

名称 图像 来源多面体 复合数量 编号 核心是
正二十面体 		星状图
五复合正四面体 正四面体 5 47 (59) 是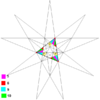
十复合正四面体 正四面体 10 22 (59)

W25

是
五复合正八面体
小星形十二面体 		正八面体 5 W51 否
截半二十面体
小星形十二面体 1
六复合五方偏方面体 五方偏方面体 6 4 (59) 是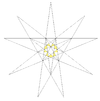
五复合正八面体 正八面体 5 是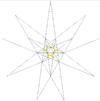

星形二十面体

[编辑]

下列表格以杜瓦（英语：Patrick du Val）记号开头字母分类。

杜瓦记号 图像 编号 名称 说明 星状图
(59) (W)
A
A 1 (59) W4 Z 正二十面体本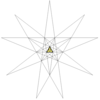身
Af2 Z Z
Af2g1 Z Z
Af2g2 Z Z
acdf2g1 Z Z
B
B 2 (59) W26
Be1 Z Z
be2 Z Z
C
C 3 (59) W23 五复合正八面体
Ce2 Z Z
Cf2g1 Z Z
D
D 4 (59) Z 六复合五方偏方面体 6个五方偏方面体的复合体（顶角藏在里面）
De1 21 (59) W32
De1f1 24 (59) Z
De1f1d 35 (59) Z
De1f1g1 25 (59) Z
De1f1df2 Z Z
De1f1df2g1 Z Z
De1f1df2g2 44 (59) Z
De1f1dg1 38 (59) Z
De1f1dg2 41 (59) Z
De1g1 Z Z
De2 27 (59) Z
De2f1d 46 (59) Z
De2f1df2g1 55 (59) Z
De2f1df2g2 58 (59) Z
De2f1dg1 49 (59) Z
De2f1f2 52 (59) Z
De2f2 30 (59) W34 大三角六边形二十面体
De2f2_ Z Z 内侧三角六边形二十面体
De2f2g2 31 (59) Z
Df1 Z Z
Df2 Z Z
E
E 5 (59) Z
Ef1 22 (59) W25 十复合正四面体
Ef1d 47 (59) W24 五复合正四面体
Ef1df2 53 (59) Z
Ef1df2g1 56 (59) Z
Ef1df2g2 59 (59) Z
Ef1dg1 50 (59) Z
Ef1g1 26 (59) W28 凹五角锥十二面体 看起来像凹十二面体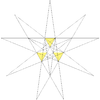
Ef1g1_ Z Z 实心凹五角锥十二面体 外观同于凹五角锥十二面体，但中心不是空的
Ef2 28 (59) 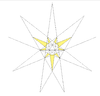Z
Ef2g2 32 (59) Z
e1 9 (59) W37
e1f1 12 (59) Z
e1f1d 34 (59) W36
e1f1df2g2 43 (59) Z
e1f1dg1 37 (59) W39
e1f1dg2 40 (59) Z
e1f1g1 13 (59) Z
e1g1 Z Z
e2 15 (59) Z
e2f1 45 (59) W40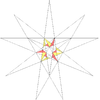
e2f1df2 51 (59) W38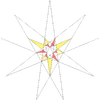
e2f1df2g1 54 (59) Z
e2f1df2g2 57 (59) Z
e2f1dg1 48 (59) Z
e2f2 18 (59) Z
e2f2g2 19 (59) Z
F
F 6 (59) W27 Ef1与De2f2的复合体
Fg1 23 (59) W31 内侧三角六边形二十面体（De2f2）与凹五角锥十二面体（Ef1g1）的复合多面体
Fg2 29 (59) W33
f1 10 (59) Z
f1d 33 (59) W35
f1df2g2 42 (59) Z
f1dg1 36 (59) Z
f1dg2 39 (59) Z
f1g1 14 (59) Z
f2 16 (59) Z
f2g2 20 (59) W30
G
G 7 (59) W41 大二十面体
g1 11 (59) W29
g2 17 (59) Z
H
H 8 (59) W42 完全星形二十面体
Hj2 Z Z 五复合立方半无穷
星形菱形六十面体 		其对偶多面体为五复合半刻面立方体
（compounds of five hemi facetted cube）

参见

[编辑]

参考文献

[编辑]
  1. ^ H·S·M·考克斯特. 五十九種二十面體. H. T. Flather, J. F. Petrie. Springer Science & Business Media. 2012. ISBN 9781461382164. 
  1. Stellation of the Icosahedron. Virtual Polyhedra, George W. Hart. 1996 [2016-03-12]. （原始内容存档于2020-02-24）. 
  2. Roman E. Maeder. Stellated Icosahedra. mathconsult.ch. 1998 [2016-03-12]. （原始内容存档于2013-09-22）. 
  3. Guy's polyhedra pages. Some lost stellations of the icosahedron. steelpillow. 2006年7月11日 [2016年3月18日]. （原始内容存档于2016年3月13日）. 

外部链接

[编辑]
检索自“https://zh.wikipedia.org/w/index.php?title=星形二十面體列表&oldid=80261778”