星形菱形三十面体
| 部分的星形菱形三十面体 | |
|---|---|
 完全星形菱形三十面体 | |
 菱形六十面体 |
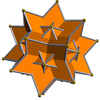 大菱形三十面体 |
在几何学中,星形菱形三十面体是指菱形三十面体的星形化体,即把菱形三十面体的面和边沿伸直到向外相交成星形的立体。温尼尔在他的书《多面体模型》中列出许多星形多面体模型,其中也收录了一些星形菱形三十面体[1],例如内侧菱形三十面体[2][3]。
历史
[编辑]星形菱形三十面体是一种多面体类型,属于此类的多面体数量非常庞大。埃德(Ede)在1958年时列举了13种基本的星形菱形三十面体类型[4]。鲍莱(Pawley)在1973年时提出了一些规则以令星形菱形三十面体可以完全被枚举[5]。
这些多面体种类繁多,大多都并未被观察及描绘,因此大多数并未命名。梅塞尔(Messer)在1995年描述了其中227个星形化体[6](含原像菱形三十面体在内,即1种凸多面体和226种星形多面体[7][8])。
种类
[编辑]菱形三十面体透过全部匹配能产生227种星形菱形三十面体[9],其中包括了115个镜像不变的立体和112个具有手性镜像的立体;透过米勒的规则[10] 可以产生358833098种星形菱形三十面体,其中包括了84959个镜像不变的立体和358748139种具有手性镜像的立体[9]。
已命名的星形菱形三十面体
[编辑]已命名的星形菱形三十面体十分少,其命名的原因多半与星形菱形三十面体无关,而是因为其他研究的同时刚好研究的立体属于星形菱形三十面体,例如五复合立方体虽是一种星形菱形三十面体[11],但其因为是立方体复合体的相关研究而得名[12]。
黄金一百二十面体
[编辑]
第一星形菱形三十面体,又称黄金一百二十面体,是菱形三十面体星形化的第一种形式,其对应形状转化为间单多面体(即去除自相交面隐没于立体内部的面)后所形成的立体共由120个面、62个顶点和180条边组成,且五种帕雷托立体皆可以共用顶点地嵌入这个立体中。[13]
黄金一百二十面体的顶点坐标都是由以下集合的元素组成[13]:
- {−φ³, −φ², −φ, 0, φ, φ², φ³}
其中,φ为黄金比例。
黄金一百二十面体的62个顶点,其中20个是来自一个正十二面体(或是为五个正四面体以两种方式重和的五复合正四面体)、5x6=30个来自5个正八面体和12个来自一个正二十面体。[13]
列表
[编辑]| 名称 | 对称群 | 图像 | 星状图 |
|---|---|---|---|
| 菱形三十面体 | Ih | 
|

|
| 黄金一百二十面体 | Ih | 
|

|
| 菱形六十面体[14] | Ih | 
|

|
| 五复合立方体[12] | Ih | 
|

|
| 内侧菱形三十面体[2] | Ih | 
|

|
| 大菱形三十面体[15] | Ih | 
|

|
| 完全星形菱形三十面体[11] | Ih | 
|

|
用途
[编辑]部分星形菱形三十面体被一些数学学者认为是具代表性的立体,用于一些与几何学相关著作的封面或标志,例如大菱形三十面体[16][15]和菱形六十面体[i][17]。前者被用于多面体领域著名著作《正多胞形》的封面上[16][15],后者为Wolfram Alpha的标志。[17]
参见
[编辑]参考文献
[编辑]- ^ Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
- ^ 2.0 2.1 Weisstein, Eric W. (编). Medial Rhombic Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语). (原始内容存档于2016-09-01).
- ^ Medial Rhombic Triacontahedron. software3d.com. (原始内容存档于2016-03-04).
- ^ Ede, J. D. "Rhombic Triacontahedra". Math. Gaz. 1958, 42: pp.98–100.
- ^ Pawley, G. S. "The 227 triacontahedra.". Geometriae Dedicata. 1975-08-01, 4 (2): pp.221–232. doi:10.1007/BF00148756.
- ^ Messer, P. W. "Stellations of the Rhombic Triacontahedron and Beyond.". Structural Topology. 1995, 21: pp.25–46.
- ^ George W. Hart. List of Stellations of the Rhombic Triacontahedron. Virtual Polyhedra. 1996 [2020-08-17]. (原始内容存档于2019-12-30).
- ^ Paulo Freire. Stellations of the Rhombic Triacontahedron. mpifr-bonn.mpg.de. 1996 [2020-08-17]. (原始内容存档于2019-05-04).
- ^ 9.0 9.1 Webb, R. "Enumeration of Stellations.". software3d.com. [2019-09-06]. (原始内容存档于2019-04-27).
- ^ Guy's. Stellation and facetting - a brief history. steelpillow.com. 2010-12-19 [2016-03-26]. (原始内容存档于2016-03-04).
- ^ 11.0 11.1 George W. Hart. Stellations of the Rhombic Triacontahedron. Virtual Polyhedra. 1996 [2020-08-17]. (原始内容存档于2019-12-29).
- ^ 12.0 12.1 Weisstein, Eric W. (编). Compound of Five Cubes. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 13.0 13.1 13.2 Lynnclaire Dennis' polyhedra. www.polyhedra-world.nc. 2005-06-25 [2022-07-30]. (原始内容存档于2022-07-30).
- ^ Weisstein, Eric W. (编). Rhombic hexecontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 15.0 15.1 15.2 Weisstein, Eric W. (编). Great rhombic triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 16.0 16.1 Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 103, 1973. ISBN 978-0486614809
- ^ 17.0 17.1 Weisstein, E. W. "the-story-of-spikey". 2018-12-28 [2020-08-20]. (原始内容存档于2020-07-18).
- 一手资料
- ^ Weisstein, E. W. "What's In a Name? That Which We Call a Rhombic Hexecontahedron.". 2009-05-19 [2020-08-20]. (原始内容存档于2020-02-15).
