第四星形二十面体
外观
(重定向自第十四星形二十面體)
 | |||||||||||||
| 类别 | 星形二十面体 收录于《五十九种二十面体》中 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 识别 | |||||||||||||
| 名称 | 第四星形二十面体 | ||||||||||||
| 参考索引 | W29, 11/59 | ||||||||||||
| 数学表示法 | |||||||||||||
| 杜瓦表示法 | g1 | ||||||||||||
| 对称性 | |||||||||||||
| 对称群 | Ih | ||||||||||||
| 图像 | |||||||||||||
| |||||||||||||
第四星形二十面体是正二十面体的一种星形化体,为正二十面体的面向外延伸并相交所形成的第四种立体,外观看起来像是仅有框架的正十二面体[1]:49,由30个双锥体组成[2]。这个立体最早由哈里·惠勒发现,[3]并认为这个立体是一个离散的结构。[2]
历史
[编辑]第四星形二十面体最早出现在哈里·惠勒发表于1924年的论文《某些形式的二十面体与特定更高多面体的推导方式》中,惠勒将其描述为形式上离散的多面体[2],并将其编号为22。[3]在1920年至1930年间,米勒定义了一套规则来规范星形二十面体,这个规则能从无限多种星形化多面体中明确定义哪些多面体是“重要且特别”的[4],当中并未排除离散或不连续的结构[5],因此在1938年哈罗德·斯科特·麦克唐纳·考克斯特、帕特里克·杜·瓦尔等人的著作《五十九种二十面体》也收录了这种立体,并编号为11。[6]
构成
[编辑]第四星形二十面体由30个双三角锥以顶点接顶点的方式,沿着正十二面体的骨架组成。[2]
-
第四星形二十面体
-
正十二面体的骨架图
-
正十二面体
组成这个立体的星形二十面体胞为第10和第12个胞。[7]
 星形二十面体中的胞 |
 第四星形二十面体的胞 |
相关多面体
[编辑]第十四星形二十面体
[编辑]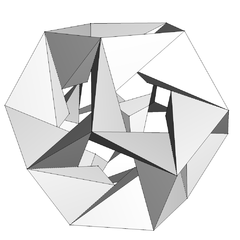 e1f1g1星形二十面体 | ||
| 类别 | 星形二十面体 收录于《五十九种二十面体》中 | |
|---|---|---|
| 识别 | ||
| 名称 | 第十四星形二十面体 | |
| 参考索引 | W39, 37/59 | |
| 数学表示法 | ||
| 杜瓦表示法 | e1f1g1 | |
| 组成与布局 | ||
| 面的种类 |  | |
| 对称性 | ||
| 对称群 | Ih | |
| 图像 | ||
| ||
第十四星形二十面体外观是一个边向某方向扭曲、且有孔洞的空心十二面体,其对称性与凹五角锥十二面体类似。[1]:61这样的结构在polyhedr.com出版的多面体组装模型产品中被评价为“魔术边”(Magic edge)。[8]
第十四星形二十面体在杜瓦记号中记为e1f1g1,不少最外层为g1的星形二十面体皆形如空心二十面体:[6]
| 名称 | 杜瓦记号 | 星状图 | 立体图 |
|---|---|---|---|
| 第四星形二十面体 11 (《五十九种二十面体》) 21(惠勒) |
g1 | 
|

|
| 13 (《五十九种二十面体》) 20(惠勒) |
e1f1g1 | 
|

|
| 14 (《五十九种二十面体》) | f1g1 |  |

|
| 25 (《五十九种二十面体》) | De1f1g1 |  |

|
| 凹五角锥十二面体 26 (《五十九种二十面体》) 9(惠勒) |
Ef1g1 | 
|

|
| 36 (《五十九种二十面体》) | f1g1 | 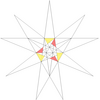 |

|
| 第十四星形二十面体 37 (《五十九种二十面体》) |
e1f1g1 | 
|

|
| 38 (《五十九种二十面体》) | De1f1g1 |  |

|
| 48 (《五十九种二十面体》) | e2f1g1 | 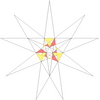 |

|
| 49 (《五十九种二十面体》) | De2f1g1 |  |

|
| 50 (《五十九种二十面体》) | Ef1g1 | 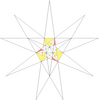 |

|
参见
[编辑]- 《五十九种二十面体》
参考文献
[编辑]- ^ 1.0 1.1 Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974. ISBN 9780521098595. LCCN 69010200.
- ^ 2.0 2.1 2.2 2.3 Inchbald, Guy. In search of the lost icosahedra. The Mathematical Gazette (Cambridge University Press). 2002, 86 (506): 208–215 [2021-09-01]. (原始内容存档于2021-06-08).
- ^ 3.0 3.1 Wheeler, Albert Harry. Certain forms of the icosahedron and a method for deriving and designating higher polyhedra. Proc. Internat. Math. Congress, Toronto. 1924, 1: 701–708.
- ^ Guy's. Stellation and facetting - a brief history. steelpillow.com. 2010-12-19 [2016-03-26]. (原始内容存档于2016-03-04).
- ^ Stellation of Polyhedra. maplesoft.com. [2020-12-15]. (原始内容存档于2020-10-25).
- ^ 6.0 6.1 Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F., The fifty-nine icosahedra 3rd, Tarquin, 1999, ISBN 978-1-899618-32-3, MR 0676126
- ^ Stellation No. 24 of the Icosahedron. mathconsult.ch. [2021-09-01]. (原始内容存档于2021-11-27).
- ^ Fourteenth stellation of icosahedron. polyhedr.com. [2021-09-01]. (原始内容存档于2022-06-27).







