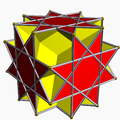
大斜方立方体
 | ||||
| 类别 | 均匀星形多面体 | |||
|---|---|---|---|---|
| 对偶多面体 | 反平行四边形二十四面体 | |||
| 识别 | ||||
| 名称 | 大斜方立方体 great rhombicube great rhombihexahedron | |||
| 别名 | 大斜方六面体 | |||
| 参考索引 | U21, C82, W103 | |||
| 鲍尔斯缩写 | groh | |||
| 数学表示法 | ||||
| 威佐夫符号 | 2 4/3 (3/2 4/2) | | |||
| 性质 | ||||
| 面 | 18 | |||
| 边 | 48 | |||
| 顶点 | 24 | |||
| 欧拉特征数 | F=18, E=48, V=24 (χ=-6) | |||
| 组成与布局 | ||||
| 面的种类 | 12个正方形 6个八角星 | |||
| 顶点图 | 4.8/3.4/3.8/5 | |||
| 对称性 | ||||
| 对称群 | Oh, [4,3], (*432) | |||
| 图像 | ||||
| ||||
大斜方立方体(great rhombicube),又称大斜方六面体(great rhombihexahedron)是一种非凸均匀多面体,由18个面、48条边和24个顶点组成。其外观与大立方截半立方体相近,差别在于大立方截半立方体的八个角落的凹陷处以及凹二面角在大斜方立方体中变为更深的凹陷坑洞[1]:158,其对偶多面体为反平行四边形二十四面体。[2]
历史
[编辑]大斜方立方体最早出现在1881年由亚伯特·巴杜罗(Albert Badoureau)描述的6种半拟正多面体(Versi-Quasi-Regular Polyhedra)中[3]。后来又被考克斯特和米勒于1930年到1932年间发现并命名。[4]
性质
[编辑]大斜方立方体共由18个面、48条边和24个顶点组成。在其18个面中有12个正方形和6个八角星面。[5]其中这些面来可以进一步地分成6个正方形面(施莱夫利符号:{4})、6个反向相接的正方形(施莱夫利符号:{4/3})、3个八角星(施莱夫利符号:{8/3})以及3个反向相接的八角星(施莱夫利符号:{8/5})[6]。大斜方立方体亦具备点可递的特性,这意味着,这立体上的任意两个顶角A和B,透过旋转或镜射这个立体,使A移动到B原来的位置时,其顶角以及其二面角仍然占据了相同的空间区域[7][8][9],换句话说,及这是一个等角立体,并具有交叉梯形的顶点图[10],其每个顶点都是2个正方形和2个八角星的公共顶点,在顶点布局中可以用4, 8/3, 4/3, 8/5来表示。[11]
大斜方立方体有两种二面角,分别为45度和90度,这两种二面角所对应的棱各24条。[5]
顶点坐标
[编辑]若大斜方立方体边长为单位长,且几何中心位于原点,则其顶点坐标为的全排列。[12]
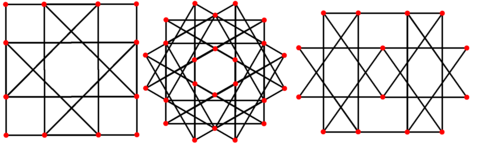
正交投影
[编辑]二面角
[编辑]大斜方立方体共有2种二面角,这两种二面角皆为正方形与八角星棱的交角。这两种二面角分别为有24个直角和24个45度角。[5]若找一个立方体,让立方体六个面与大斜方立方体的六个八角星面平行,则这个大斜方立方体靠近立方体棱中央附近的二面角为直角,其余二面角为45度角。更精确地说,所有大斜方立方体位于伪三角形(pseudo {3})的二面角为直角;位于伪四边形(pseudo {4})的二面角为45度角。[13]
定向性
[编辑]大斜方立方体的表面是一个不可定向的曲面[11],即无法定义表面上特定点属于内部或外部,因为任何点都可以在不打洞的情况下经由表面找到一个路径连接该点对应的背面的位置,这个特性与克莱因瓶类似[10]。
相关多面体
[编辑]大斜方立方体与截角立方体共用相同的顶点布局[13]。其亦与非凸大斜方立方八面体和大立方截半立方体有着相同的棱布局。[13]
 截角立方体 |
 非凸大斜方立方八面体 |
 大立方截半立方体 |
 大斜方六面体 |
对偶多面体
[编辑]
大斜方立方体由18个面、48条边和24个顶点组成,因此对应的对偶多面体之面的几何中心将会对应到原始多面体的顶点,也就是说大斜方立方体的对偶多面体为一种二十四面体。这种二十四面体由24个全等的反平行四边形组成,共有24个面、48条边和18个顶点[14]。
参见
[编辑]参考文献
[编辑]- ^ Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- ^ Weisstein, Eric W. (编). Great Rhombihexacron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Jean Paul Albert Badoureau. Mémoire sur les Figures Isocèles. Journal de l'École polytechnique. 1881, (49): 47-172.
- ^ H. S. M. Coxeter; M. S. Longuet-Higgins; J. C. P. Miller. Uniform Polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 1954, 246: 401–450.
- ^ 5.0 5.1 5.2 David I. McCooey. Versi-Quasi-Regular Polyhedra : Great Rhombihexahedron. dmccooey.com. [2021-09-05]. (原始内容存档于2019-01-07).
- ^ Weisstein, Eric W. (编). Great Rhombihexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 371 Transitivity
- ^ Grünbaum, Branko; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (6.4 Isotoxal tilings, 309-321)
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., Uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
- ^ 10.0 10.1 David I. McCooey. Versi-Quasi-Regular Polyhedra. dmccooey.com. [2021-09-05]. (原始内容存档于2020-06-18).
- ^ 11.0 11.1 Maeder, Roman. 21: great rhombihexahedron. MathConsult. [2021-09-11]. (原始内容存档于2020-02-17).
- ^ David I. McCooey. Data of Great Rhombihexahedron. dmccooey.com. [2021-09-05]. (原始内容存档于2021-09-11).
- ^ 13.0 13.1 13.2 Klitzing, Richard. great rhombihexahedron : groh. bendwavy.org. [2021-09-05]. (原始内容存档于2021-08-09).
- ^ David I. McCooey. Versi-Quasi-Regular Duals: Great Rhombihexacron. dmccooey.com. [2019-09-07]. (原始内容存档于2018-03-10).