此条目页的主题是物理量。关于电路元件，请见“
电容器 ”。
感受到电容器 两端的电势差 ，正电荷与负电荷会分别累积于两片平行薄板导体。 在电路学 里，给定电压 ，电容器 储存电荷 的能力，称为电容 （英语：capacitance ），标记为C 。采用国际单位制 ，电容的单位是法拉 （farad ），标记为F 。
平行板电容器 是一种简单的电容器，是由互相平行、以空间或介电质 隔离的两片薄板导体 构成。假设这两片导板分别载有负电荷与正电荷，所载有的电荷量分别为
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
V
{\displaystyle V}
C
{\displaystyle C}
C
=
Q
V
{\displaystyle C={\frac {Q}{V}}}
由上式知1法拉（Farad）等于1库仑 （Coulomb）每伏特 （Voltage）。在正常状况下1法拉的电容多加1伏特的电势差可以多储存1库仑的电荷。
电容器所储存的能量等于充电所做的功 。思考前述平行板电容器，搬移微小电荷元素
d
q
{\displaystyle \mathrm {d} q}
d
W
{\displaystyle \mathrm {d} W}
d
W
=
q
C
d
q
{\displaystyle \mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q}
将这方程积分，可以得到储存于电容器的能量。从尚未充电的电容器（
q
=
0
{\displaystyle q=0}
−
Q
{\displaystyle -Q}
+
Q
{\displaystyle +Q}
W
{\displaystyle W}
W
charging
=
∫
0
Q
q
C
d
q
=
Q
2
2
C
=
1
2
C
V
2
=
U
stored
{\displaystyle W_{\text{charging}}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {Q^{2}}{2C}}={\frac {1}{2}}CV^{2}=U_{\text{stored}}}
其中，
U
stored
{\displaystyle U_{\text{stored}}}
电容的单位是法拉，简称“法”，单位符号为“F”，是国际单位制导出单位 [ 1] 库仑 除以一伏特 。一般来说，1法拉算是很大的电容，大多数用于电子电路 的电容器，其电容会小于法拉几个数量级，常用的单位有“微法拉”（microfarad，μF），等于
10
−
6
{\displaystyle 10^{-6}}
10
−
9
{\displaystyle 10^{-9}}
微波 工程领域中，有时会使用到较小的“皮法拉”（picofarad，pF），等于
10
−
12
{\displaystyle 10^{-12}}
10
−
15
{\displaystyle 10^{-15}}
1
F
=
10
6
μ
F
=
10
9
n
F
=
10
12
p
F
=
10
15
f
F
.
{\displaystyle 1F=10^{6}\mu F=10^{9}nF=10^{12}pF=10^{15}fF.}
[ 2]
假设，给定电容器的几何形状和电容器内部的介质性质，则可以计算出电容。如前图所示，假设平行板电容器的两片导板的面积都是
A
{\displaystyle A}
d
{\displaystyle d}
−
σ
{\displaystyle -\sigma }
+
σ
{\displaystyle +\sigma }
σ
=
Q
/
A
{\displaystyle \sigma =Q/A}
应用高斯定律 （详尽细节，请参阅条目电位移 ），在两片导板之间的电场
E
{\displaystyle E}
E
=
σ
/
ε
=
Q
/
ε
A
{\displaystyle E=\sigma /\varepsilon =Q/\varepsilon A}
其中，
ε
{\displaystyle \varepsilon }
电容率 。
两片导板的电势差为
V
=
E
d
=
σ
d
/
ε
=
Q
d
/
ε
A
{\displaystyle V=Ed=\sigma d/\varepsilon =Qd/\varepsilon A}
所以，电容为
C
=
Q
/
V
=
ε
A
/
d
{\displaystyle C=Q/V=\varepsilon A/d}
电容与导板面积A成正比，与导板间隔距离d呈反比，这是在假设平板电容器的面积A相当大的情况下，可以忽略电容器边缘的效应。假设间隔距离
d
{\displaystyle d}
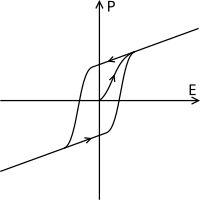
铁电性物质的电极化强度
P
{\displaystyle P}
E
{\displaystyle E}
迟滞现象 。 许多常用的电介质，其电容率 会随着外电场的变化而改变，是外电场的函数。铁电性 物质就是这种电介质。使用这种电介质的电容器，其电容会比较复杂。例如，当这种电容器在充电时，电荷与电压（电势差）的关系为
d
Q
=
C
(
V
)
d
V
{\displaystyle \mathrm {d} Q=C(V)\ \mathrm {d} V}
在上述方程里，电容对于电压的依赖性
C
(
V
)
{\displaystyle C(V)}
E
=
V
/
d
{\displaystyle E=V/d}
这电场将电介质电极化，从而增加导板储存电荷的能力。如右图所示，对于铁电性物质，电极化强度 对电场曲线显示出迟滞现象 [ 3] [ 4]
假设电极化强度
P
{\displaystyle P}
P
=
f
(
E
)
=
f
(
V
/
d
)
=
g
(
V
)
{\displaystyle P=f(E)=f(V/d)=g(V)}
其中，
f
(
E
)
{\displaystyle f(E)}
g
(
V
)
{\displaystyle g(V)}
well-behaved function ）。
根据电位移
D
{\displaystyle D}
D
=
P
+
ϵ
0
E
=
g
(
V
)
+
ϵ
0
V
/
d
{\displaystyle D=P+\epsilon _{0}E=g(V)+\epsilon _{0}V/d}
应用自由电荷高斯定律 ，导板载有的电荷量为
Q
=
D
A
=
(
g
(
V
)
+
ϵ
0
V
/
d
)
A
{\displaystyle Q=DA=(g(V)+\epsilon _{0}V/d)A}
所以，电容为
C
(
V
)
=
Q
V
=
g
(
V
)
A
V
+
ϵ
0
A
d
{\displaystyle C(V)={\frac {Q}{V}}={\frac {g(V)A}{V}}+{\frac {\epsilon _{0}A}{d}}}
假设
g
(
V
)
{\displaystyle g(V)}
g
(
V
)
=
k
V
{\displaystyle g(V)=kV}
k
{\displaystyle k}
C
=
Q
V
=
k
A
+
ϵ
0
A
d
{\displaystyle C={\frac {Q}{V}}=kA+{\frac {\epsilon _{0}A}{d}}}
否则，假设
g
(
V
)
{\displaystyle g(V)}
继续思考这跟电压有关的电容，假若将电容器充电至电压
V
{\displaystyle V}
+
Q
{\displaystyle +Q}
−
Q
{\displaystyle -Q}
Q
=
∫
0
V
C
(
V
′
)
d
V
′
{\displaystyle Q=\int _{0}^{V}C(V')\ \mathrm {d} V'}
当电容与电压无关时，这方程变为
Q
=
C
V
{\displaystyle Q=CV}
储存于电容器 的微分 能量 为
d
U
stored
=
Q
d
V
″
=
[
∫
0
V
″
C
(
V
′
)
d
V
′
]
d
V
″
{\displaystyle \mathrm {d} U_{\text{stored}}=Q\mathrm {d} V''=\left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''}
应用分部积分法 ：
∫
a
z
f
(
x
)
g
′
(
x
)
d
x
=
[
f
(
x
)
g
(
x
)
]
a
z
−
∫
a
z
f
′
(
x
)
g
(
x
)
d
x
{\displaystyle \int _{a}^{z}f(x)g'(x)\ \mathrm {d} x=\left[f(x)g(x)\right]_{a}^{z}-\int _{a}^{z}f'(x)g(x)\ \mathrm {d} x}
分别设定
f
(
x
)
=
∫
a
x
h
(
y
)
d
y
{\displaystyle f(x)=\int _{a}^{x}\ h(y)\ \mathrm {d} y}
g
(
x
)
=
x
{\displaystyle g(x)=x}
∫
a
z
∫
a
x
h
(
y
)
d
y
d
x
=
[
∫
a
x
x
h
(
y
)
d
y
]
a
z
−
∫
a
z
x
h
(
x
)
d
x
=
∫
a
z
z
h
(
y
)
d
y
−
∫
a
z
y
h
(
y
)
d
y
=
∫
a
z
(
z
−
y
)
h
(
y
)
d
y
{\displaystyle \int _{a}^{z}\int _{a}^{x}\ h(y)\ \mathrm {d} y\ \mathrm {d} x=\left[\int _{a}^{x}\ xh(y)\ \mathrm {d} y\right]_{a}^{z}-\int _{a}^{z}xh(x)\ \mathrm {d} x=\int _{a}^{z}zh(y)\ \mathrm {d} y-\int _{a}^{z}yh(y)\ \mathrm {d} y=\int _{a}^{z}\ \left(z-y\right)h(y)\ \mathrm {d} y}
设定
x
=
V
″
{\displaystyle x=V''}
y
=
V
′
{\displaystyle y=V'}
h
(
y
)
=
C
(
V
′
)
{\displaystyle h(y)=C(V')}
a
=
0
{\displaystyle a=0}
z
=
V
{\displaystyle z=V}
U
stored
=
∫
0
V
[
∫
0
V
″
C
(
V
′
)
d
V
′
]
d
V
″
=
∫
0
V
(
V
−
V
′
)
C
(
V
′
)
d
V
′
{\displaystyle U_{\text{stored}}=\int _{0}^{V}\ \left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''=\int _{0}^{V}\ \left(V-V'\right)C(V')\ \mathrm {d} V'}
扫描非线性介质显微镜 （scanning nonlinear dielectric microscope ）的探针扫描于铁电性物质表面所测量到的非线性电容，可以用来研究铁电性物质的铁电畴（ferroelectric domain ）结构[ 5]
有些半导体元件 的电容可以用电压控制。例如，当变容二极管 的逆向偏压增加时，空乏层厚度也会增加，因而使得电容降低[ 6]
假若电容器两端驱动的含时电压变化太快，则电介质的电极化强度可能会无法跟上讯号。从微观层次解释这机制，在电介质内部，决定电容率的微小电偶极子 无法瞬时地移动，因此，当施加的交流电压的频率增加时，电偶极子只能给出有限的响应，从而造成电容率 降低。电容率与频率的关系称为介电色散 （dielectric dispersion ），是由介电弛豫 （dielectric relaxation ）过程所主控，像德拜弛豫 （Debye relaxation ）。从更基本的微观分析来计算，例如对于介质内的电偶极子行为的微观分析，处于暂态状况，电位移场可以表达为（更详尽细节，请参阅电极化率 ）
D
(
t
)
=
ε
0
2
π
∫
−
∞
t
d
t
′
ε
r
(
t
−
t
′
)
E
(
t
′
)
{\displaystyle {\boldsymbol {D}}(t)={\frac {\varepsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{t}\mathrm {d} t'\ \varepsilon _{r}(t-t'){\boldsymbol {E}}(t')}
其中，
ε
0
{\displaystyle \varepsilon _{0}}
电常数 ，
ε
r
=
d
e
f
ε
/
ε
0
{\displaystyle \varepsilon _{r}\ {\stackrel {def}{=}}\ \varepsilon /\varepsilon _{0}}
相对电容率 。
相对电容率的时间依赖可以用线性响应函数 （linear response function ）来描述[ 7]
Δ
t
<
0
{\displaystyle \Delta t<0\,\!}
ε
r
(
Δ
t
)
=
0
{\displaystyle \varepsilon _{r}(\Delta t)=0\,\!}
D
(
t
)
=
ε
0
2
π
∫
−
∞
∞
d
t
′
ε
r
(
t
−
t
′
)
E
(
t
′
)
{\displaystyle {\boldsymbol {D}}(t)={\frac {\varepsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathrm {d} t'\ \varepsilon _{r}(t-t'){\boldsymbol {E}}(t')}
对于时间做傅里叶变换 ，根据折积定理 ，可以得到
D
(
ω
)
=
ε
0
ε
r
(
ω
)
E
(
ω
)
{\displaystyle {\boldsymbol {D}}(\omega )=\varepsilon _{0}\varepsilon _{r}(\omega ){\boldsymbol {E}}(\omega )}
其中，
ω
{\displaystyle \omega }
角频率 。
ε
r
(
ω
)
{\displaystyle \varepsilon _{r}(\omega )}
复函数 ，其虚值部分与介质的电场能量吸收有关。更详尽细节，请参阅条目电容率 。由于电容与电容率成正比，电容也具有这频率行为。对于时间做傅里叶变换于高斯定律：
Q
(
ω
)
=
∮
S
D
(
r
,
ω
)
⋅
d
a
{\displaystyle Q(\omega )=\oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} }
其中，
S
{\displaystyle \mathbb {S} }
Q
{\displaystyle Q}
S
{\displaystyle \mathbb {S} }
r
{\displaystyle \mathbf {r} }
d
a
{\displaystyle \mathrm {d} \mathbf {a} }
流入闭曲面
S
{\displaystyle \mathbb {S} }
I
(
t
)
=
d
Q
d
t
{\displaystyle I(t)={\frac {dQ}{dt}}}
I
(
ω
)
=
j
ω
Q
(
ω
)
=
j
ω
∮
S
D
(
r
,
ω
)
⋅
d
a
=
[
G
(
ω
)
+
j
ω
C
(
ω
)
]
V
(
ω
)
=
V
(
ω
)
Z
(
ω
)
{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} \\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\\\end{aligned}}}
其中，
j
{\displaystyle j}
虚数单位 ，
G
(
ω
)
{\displaystyle G(\omega )}
C
(
ω
)
{\displaystyle C(\omega )}
V
(
ω
)
{\displaystyle V(\omega )}
Z
(
ω
)
{\displaystyle Z(\omega )}
电导 、电容、电压、复值阻抗 。
假设平行板电容器的两片导板之间填满了电介质，按照下述关系式，电介质的性质可以测量出来[ 8]
ε
r
(
ω
)
=
ε
r
′
(
ω
)
−
j
ε
r
″
(
ω
)
=
1
j
ω
Z
(
ω
)
C
0
=
C
(
ω
)
C
0
{\displaystyle \varepsilon _{r}(\omega )=\varepsilon _{r}'(\omega )-j\varepsilon _{r}''(\omega )={\frac {1}{j\omega Z(\omega )C_{0}}}={\frac {C(\omega )}{C_{0}}}}
其中，
ε
r
′
(
ω
)
{\displaystyle \varepsilon _{r}'(\omega )}
ε
r
″
(
ω
)
{\displaystyle \varepsilon _{r}''(\omega )}
C
(
ω
)
{\displaystyle C(\omega )}
C
0
{\displaystyle C_{0}}
自由空间 时的电容）。
深能级暂态谱学 （deep-level transient spectroscopy ）利用电容的时间响应来研究半导体 的深能级缺陷[ 9] 能隙 的位置，缺陷分类为浅能级缺陷和深能级缺陷。浅能级缺陷的能级离导带 或价带 的能带 边缘比较近，在0.1eV以内，处于这能级的电子或空穴很容易因热运动而变成自由电子或自由空穴；一般而言，深能级缺陷离能带边缘比较远，超过0.1eV。但也有些物质的深能级缺陷离能带边缘虽然只有0.001eV，仍旧能够显示出深能级缺陷的通常性质[ 10]
金属氧化物半导体电容器 （MOS capacitor ）是另一个电容与频率有关的例子。对于这案例，少数载流子 的缓慢生成意味着在高频率状况，只有多数载流子 的响应能够贡献出电容，而在低频率状况，两种载流子的响应都能够贡献出电容[ 11] [ 9]
当频率为光学 频率时，半导体 的电容会展示出类似固体的能带结构。精密的调制光谱学 （modulation spectroscopy ）测量方法，使用压力 或其它种应力 来调制晶体结构，然后观测光波的吸收或反射的相关变化。这方法贡献出很多关于这些物质的性质的结果[ 12]
前面论述的范围局限于两片任意尺寸、形状的平行导板的案例。对于单独的带电导板，电容的定义方程
C
=
d
e
f
Q
/
V
{\displaystyle C\ {\stackrel {def}{=}}\ Q/V}
对于多个导体的案例，或当两个导体所带净电荷量不等于零的案例，方程
C
=
Q
/
V
{\displaystyle C=Q/V}
詹姆斯·麦克斯韦 提出了“电势系数”和“感应系数”（coefficients of induction ）的概念[ 13]
Q
1
{\displaystyle Q_{1}}
Q
2
{\displaystyle Q_{2}}
Q
3
{\displaystyle Q_{3}}
电势
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
V
3
{\displaystyle V_{3}}
V
1
=
P
11
Q
1
+
P
12
Q
2
+
P
13
Q
3
{\displaystyle V_{1}=P_{11}Q_{1}+P_{12}Q_{2}+P_{13}Q_{3}}
V
2
=
P
21
Q
1
+
P
22
Q
2
+
P
23
Q
3
{\displaystyle V_{2}=P_{21}Q_{1}+P_{22}Q_{2}+P_{23}Q_{3}}
V
3
=
P
31
Q
1
+
P
32
Q
2
+
P
33
Q
3
{\displaystyle V_{3}=P_{31}Q_{1}+P_{32}Q_{2}+P_{33}Q_{3}}
其中，
P
i
j
{\displaystyle P_{ij}}
i
,
j
=
1
,
2
,
3
{\displaystyle i,j=1,2,3}
解析这线性方程组 ，可以得到电荷量分别为
Q
1
=
C
11
V
1
+
C
12
V
2
+
C
13
V
3
{\displaystyle Q_{1}=C_{11}V_{1}+C_{12}V_{2}+C_{13}V_{3}}
Q
2
=
C
21
V
1
+
C
22
V
2
+
C
23
V
3
{\displaystyle Q_{2}=C_{21}V_{1}+C_{22}V_{2}+C_{23}V_{3}}
Q
3
=
C
31
V
1
+
C
32
V
2
+
C
33
V
3
{\displaystyle Q_{3}=C_{31}V_{1}+C_{32}V_{2}+C_{33}V_{3}}
其中，
C
i
i
{\displaystyle C_{ii}}
i
{\displaystyle i}
C
i
j
{\displaystyle C_{ij}}
i
≠
j
{\displaystyle i\neq j}
延伸至
n
{\displaystyle n}
V
i
=
∑
j
=
1
n
P
i
j
Q
j
,
i
=
1
,
2
,
…
,
n
{\displaystyle V_{i}=\sum _{j=1}^{n}P_{ij}Q_{j},\qquad \qquad i=1,2,\dots ,n}
Q
i
=
∑
j
=
1
n
C
i
j
V
j
,
i
=
1
,
2
,
…
,
n
{\displaystyle Q_{i}=\sum _{j=1}^{n}C_{ij}V_{j},\qquad \qquad i=1,2,\dots ,n}
设定第
i
{\displaystyle i}
i
{\displaystyle i}
这样，整个系统可以用一组系数来描述，称为“倒电容矩阵”，以方程定义为
P
i
j
=
d
e
f
∂
V
i
∂
Q
j
{\displaystyle P_{ij}\ {\stackrel {def}{=}}\ {\frac {\partial V_{i}}{\partial Q_{j}}}}
整个系统又可以用另一组系数来描述，称为“电容矩阵”，以方程定义为
C
i
j
=
d
e
f
∂
Q
i
∂
V
j
{\displaystyle C_{ij}\ {\stackrel {def}{=}}\ {\frac {\partial Q_{i}}{\partial V_{j}}}}
赫尔曼·冯·亥姆霍兹 和威廉·汤姆森 证明这些电势系数与感应系数都具有对称性[ 13]
P
i
j
=
P
j
i
{\displaystyle P_{ij}=P_{ji}}
C
i
j
=
C
j
i
{\displaystyle C_{ij}=C_{ji}}
对于这
n
{\displaystyle n}
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
Q
{\displaystyle Q\,\!}
[ 14]
C
=
d
e
f
Q
/
Δ
V
{\displaystyle C\ {\stackrel {def}{=}}\ Q/\Delta V}
假设第
i
{\displaystyle i}
j
{\displaystyle j}
−
Q
{\displaystyle -Q\,\!}
+
Q
{\displaystyle +Q\,\!}
i
{\displaystyle i}
j
{\displaystyle j}
V
i
=
−
P
i
i
Q
+
P
i
j
Q
{\displaystyle V_{i}=-P_{ii}Q+P_{ij}Q}
V
j
=
−
P
j
i
Q
+
P
j
j
Q
{\displaystyle V_{j}=-P_{ji}Q+P_{jj}Q}
这两个导体的电容为
C
=
Q
/
(
V
j
−
V
i
)
=
1
/
(
P
i
i
+
P
j
j
−
2
P
i
j
)
{\displaystyle C=Q/(V_{j}-V_{i})=1/(P_{ii}+P_{jj}-2P_{ij})}
在电路学 里，电容通常是术语“互电容”（mutual capacitance ）的简称，即两个邻近导体（像平行板电容器的两片薄板）之间的电容。另外还有一种电路学性质术语“自电容”（self-capacitance ），即单独导体的电势每增加1V所需的电荷量。设定这电势等于零的参考点为一个理论球壳导体，其半径为无穷远，其球心与单独导体同位置。假设这单独导体是半径为
R
{\displaystyle R}
V
=
Q
/
4
π
ε
0
R
{\displaystyle V=Q/4\pi \varepsilon _{0}R}
其自电容是[ 15]
C
=
Q
/
V
=
4
π
ε
0
R
{\displaystyle C=Q/V=4\pi \varepsilon _{0}R}
范德格拉夫起电机 顶端的圆球形金属导体，其半径通常为20 cm，这金属导体的自电容为
C
=
4
π
ε
0
R
=
4
π
×
8.85
×
10
−
12
×
0.2
≈
22
[
p
F
]
{\displaystyle C=4\pi \varepsilon _{0}R=4\pi \times 8.85\times 10^{-12}\times 0.2\approx 22[pF]}
地球的半径约为6.378×106 m，其自电容为
C
=
4
π
×
8.85
×
10
−
12
×
6.378
×
10
6
≈
700
[
μ
F
]
{\displaystyle C=4\pi \times 8.85\times 10^{-12}\times 6.378\times 10^{6}\approx 700[\mu F]}
任意两个相邻导体，除非长久保持很近的距离，其电容通常很微小，但仍旧可以被视为电容器。这不受欢迎的效应称为“杂散电容”。原本各自孤立的电路，由于杂散电容的作用，可能会让两个电路互相干扰对方的信号，这效应称为串扰 。杂散电容是电路在短波波段 正常操作的限制因子。
为了消除跟远方形成的杂散电容，可以将电路装置于金属机壳内，再将金属机壳跟地线 连结。
欲求得一个系统的电容，必须先解析拉普拉斯方程
∇
2
ϕ
=
0
{\displaystyle \nabla ^{2}\phi =0}
ϕ
{\displaystyle \phi }
对于准二维问题，不同的几何构形之间可以用解析函数互相映射 。详尽细节，请参阅条目施瓦茨-克里斯托费尔映射
电容的英文也称为Capacity。但现在Capacity又另有电量 的意思。[ 23]
^ 中华人民共和国国务院. 中华人民共和国法定计量单位 . 维基文库 . 1984-02-27. ^ 韩瑞功 2004 ，第6页 harvnb模板错误: 无指向目标: CITEREF韩瑞功2004 (帮助 ) ^ Carlos Paz de Araujo, Ramamoorthy Ramesh, George W Taylor (Editors). Science and Technology of Integrated Ferroelectrics: Selected Papers from Eleven Years of the Proceedings of the International Symposium on Integrated Ferroelectrics. CRC Press. 2001. pp. 508–510, Figure 6, 7. ^ Solomon Musikant. What Every Engineer Should Know about Ceramics. CRC Press. 1991: pp. 43, Figure 3.8. ISBN 0824784987 ^ Yasuo Cho. Scanning Nonlinear Dielectric Microscope in Polar Oxides ; R Waser, U Böttger & S Tiedke, editors. Wiley-VCH. 2005. Chapter 16. ISBN 3527405321 ^ Simon M. Sze, Kwok K. Ng. Physics of Semiconductor Devices 3rd Edition. Wiley. 2006. Figure 25, p. 121. ISBN 0470068302 ^ Gabriele Giuliani, Giovanni Vignale. Quantum Theory of the Electron Liquid . Cambridge University Press. 2005: 111 . ISBN 0521821126 ^ Horst Czichos, Tetsuya Saito, Leslie Smith. Springer Handbook of Materials Measurement Methods . Springer. 2006: 475 . ISBN 3540207856 ^ 9.0 9.1 Kasap, Safa; Capper, Peter, Springer handbook of electronic and photonic materials illustrated, Springer: pp. 425, 434–436, 2006, ISBN 9780387260594 ^ Schulz, Max (编), Impurities and defects in Group IV elements and III-V compounds illustrated, Springer: pp. 12 ,68, 1999, ISBN 978-3540179177 ^ Simon M. Sze, Kwok K. Ng. Physics of Semiconductor Devices 3rd Edition. Wiley. 2006: 217. ISBN 0470068302 ^ PY Yu and Manuel Cardona. Fundamentals of Semiconductors 3rd Edition. Springer. 2001: §6.6 Modulation Spectroscopy. ISBN 3540254706 ^ 13.0 13.1 麦克斯韦, 詹姆斯 , 3, A treatise on electricity and magnetism, Volume 1 , Clarendon Press: pp. 88ff, 1873 ^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 43, 88(problem 2.8), 136(problem 3.3), 1999, ISBN 978-0-471-30932-1 ^ 新南威尔士大学 物理系讲义：电容与电介质 互联网档案馆 的存档 ，存档日期2009-02-26.^ 16.0 16.1 Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 88, 1999, ISBN 978-0-471-30932-1 ^ Jackson, J. D. Classical Electrodynamics. Wiley. 1975: 80. ^ Binns; Lawrenson. Analysis and computation of electric and magnetic field problems . Pergamon Press. 1973 [2010-06-04 ] . ISBN 978-0-08-016638-4 ^ 19.0 19.1 Maxwell, J. C. A Treatise on Electricity and Magnetism . Dover. 1873: 266 ff. ISBN 0-486-60637-6 ^ Rawlins, A. D. Note on the Capacitance of Two Closely Separated Spheres. IMA Journal of Applied Mathematics. 1985, 34 (1): 119–120. doi:10.1093/imamat/34.1.119 ^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 136, problem 3.3, 1999, ISBN 978-0-471-30932-1 ^ Jackson, J. D. Charge density on thin straight wire, revisited. Am. J. Phys. 200, 68 (9): 789–799. doi:10.1119/1.1302908 ^ Capacity | Definition of Capacity by Merriam-Webster . [2021-01-02 ] . （原始内容 存档于2021-05-09）.
此条目页的主题是物理量。关于电路元件，请见“电容器”。
![{\displaystyle \mathrm {d} U_{\text{stored}}=Q\mathrm {d} V''=\left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb1d2a38f0054ef11a42860b809646552c2ebac)
![{\displaystyle \int _{a}^{z}f(x)g'(x)\ \mathrm {d} x=\left[f(x)g(x)\right]_{a}^{z}-\int _{a}^{z}f'(x)g(x)\ \mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69a9b2585fbf8bcdf0ee5d636114b1d4396dcab4)
![{\displaystyle \int _{a}^{z}\int _{a}^{x}\ h(y)\ \mathrm {d} y\ \mathrm {d} x=\left[\int _{a}^{x}\ xh(y)\ \mathrm {d} y\right]_{a}^{z}-\int _{a}^{z}xh(x)\ \mathrm {d} x=\int _{a}^{z}zh(y)\ \mathrm {d} y-\int _{a}^{z}yh(y)\ \mathrm {d} y=\int _{a}^{z}\ \left(z-y\right)h(y)\ \mathrm {d} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf9b9e7b988b1c4db9585e9db925e22393c63765)
![{\displaystyle U_{\text{stored}}=\int _{0}^{V}\ \left[\int _{0}^{V''}\ C(V')\ \mathrm {d} V'\right]\mathrm {d} V''=\int _{0}^{V}\ \left(V-V'\right)C(V')\ \mathrm {d} V'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582babe2af74f1f54ccecee4c5216f2a9a10aedb)
![{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\mathbb {S} }\mathbf {D} (\mathbf {r} ,\omega )\cdot \mathrm {d} \mathbf {a} \\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7facbc4096d73e8bcde1f953fb0871a3552300)
![{\displaystyle C=4\pi \varepsilon _{0}R=4\pi \times 8.85\times 10^{-12}\times 0.2\approx 22[pF]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33051a38031b72c48c405d897fde7f3b92bc7928)
![{\displaystyle C=4\pi \times 8.85\times 10^{-12}\times 6.378\times 10^{6}\approx 700[\mu F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41fed4732f0cf350e3c3eb275df407b1934fae48)
![{\displaystyle {\frac {2\pi \varepsilon l}{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4d56c633ce773c15c52403b1f8c185a95bbbbc)
中华人民共和国法定计量单位. 维基文库. 1984-02-27.
