在积分学中,椭圆积分最初出现于椭圆的弧长有关的问题中。朱利奥·法尼亚诺和欧拉是最早的研究者。现代数学将椭圆积分定义为可以表达为如下形式的任何函数  的积分
的积分
![{\displaystyle f(x)=\int _{c}^{x}R[t,{\sqrt[{}]{P(t)}}]\ dt\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64997726d1cd7063eddda9718a71431e3a23789)
其中 是其两个参数的有理函数,
是其两个参数的有理函数, 是一个无重根的
是一个无重根的 或
或 阶多项式,而
阶多项式,而 是一个常数。
是一个常数。
通常,椭圆积分不能用基本函数表达。这个一般规则的例外出现在 有重根的时候,或者是
有重根的时候,或者是 ,
, 没有
没有 的奇数幂时。但是,通过适当的简化公式,每个椭圆积分可以变为只涉及有理函数和三个经典形式的积分。(也即,第一,第二,和第三类的椭圆积分)。
的奇数幂时。但是,通过适当的简化公式,每个椭圆积分可以变为只涉及有理函数和三个经典形式的积分。(也即,第一,第二,和第三类的椭圆积分)。
除下面给出的形式之外,椭圆积分也可以表达为勒让德形式和Carlson对称形式。通过对施瓦茨-克里斯托费尔映射的研究可以加深对椭圆积分理论的理解。历史上,椭圆函数是作为椭圆积分的逆函数被发现的,特别是这一个:![{\displaystyle F[{\textrm {sn}}\left(z;k\right);k]=z\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c66802524275339337594efabdd82b3dd6fb86) 其中
其中 是雅可比正弦椭圆函数。
是雅可比正弦椭圆函数。
椭圆积分通常表述为不同变量的函数。这些变量完全等价(它们给出同样的椭圆积分),但是它们看起来很不相同。很多文献使用单一一种标准命名规则。在定义积分之前,先来检视一下这些变量的命名常规:
 模角;
模角; 椭圆模;
椭圆模; 参数;
参数;
上述三种常规完全互相确定。规定其中一个和规定另外一个一样。椭圆积分也依赖于另一个变量,可以有如下几种不同的设定方法:
 幅度
幅度 其中
其中
 ,其中
,其中 而
而 是雅可比椭圆函数之一
是雅可比椭圆函数之一
规定其中一个决定另外两个。这样,它们可以互换地使用。注意 也依赖于
也依赖于 。其它包含
。其它包含 的关系有
的关系有

和

后者有时称为δ幅度并写作 。有时文献也称之为补参数,补模或者补模角。这些在四分周期中有进一步的定义。
。有时文献也称之为补参数,补模或者补模角。这些在四分周期中有进一步的定义。
第一类不完全椭圆积分  定义为
定义为

与此等价,用雅可比的形式,可以设
 ;则
;则

其中,假定任何有竖直条出现的地方,紧跟竖直条的变量是(如上定义的)参数;而且,当反斜杠出现的时候,跟着出现的是模角。
在这个意义下, ,这里的记法来自标准参考书Abramowitz and Stegun。
,这里的记法来自标准参考书Abramowitz and Stegun。
但是,还有许多不同的用于椭圆积分的记法。取值为椭圆积分的函数没有(像平方根,正弦和误差函数那样的)标准和唯一的名字。甚至关于该领域的文献也常常采用不同的记法。Gradstein, Ryzhik[1] (页面存档备份,存于互联网档案馆),  .(8.111)]采用
.(8.111)]采用 。该记法和这里的
。该记法和这里的 ;以及下面的
;以及下面的 等价。
等价。
和上面的不同对应的是,如果从Mathematica语言翻译代码到Maple语言,必须将EllipticK函数的参数用它的平方根代替。反过来,如果从Maple翻到Mathematica,则参数应该用它的平方代替。Maple中的EllipticK( )几乎和Mathematica中的EllipticK[
)几乎和Mathematica中的EllipticK[ ]相等;至少当
]相等;至少当 时是相等的。
时是相等的。
注意

其中 如上文所定义:由此可见,雅可比椭圆函数是椭圆积分的逆。
如上文所定义:由此可见,雅可比椭圆函数是椭圆积分的逆。
![{\displaystyle \forall \varphi _{1},\varphi _{2}\in \left]-{\frac {\pi }{2}};{\frac {\pi }{2}}\right[,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/989fec711a792ee800b77b31e2335eac09a567cf)

![{\displaystyle \arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\in [-\pi /2;\pi /2]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbce7940dbd301d450a8df8f9e5ec059be6184d5)

![{\displaystyle \arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\in [0;\pi ]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/847d9b225998e6ff4e6ba2417215602b7344d425)











第二类不完全椭圆积分  是
是

与此等价,采用另外一个记法(作变量替换 ),
),

其它关系包括


![{\displaystyle \forall \varphi _{1},\varphi _{2}\in \left]-{\frac {\pi }{2}};{\frac {\pi }{2}}\right[,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/989fec711a792ee800b77b31e2335eac09a567cf)
![{\displaystyle \textstyle E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42b85802f1d5c5d1662a33f4d575098caf657bd)





第三类不完全椭圆积分 是
是

或者

或者

数字 称为特征数,可以取任意值,和其它参数独立。但是要注意
称为特征数,可以取任意值,和其它参数独立。但是要注意 对于任意
对于任意 是无穷的。
是无穷的。
![{\displaystyle \Pi (n;\phi _{1},k)+\Pi (n;\phi _{2},k)=\Pi \left[n;\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}},k\right]-{\sqrt {\frac {n}{(1-n)(n-k^{2})}}}\arctan {\frac {{\sqrt {(1-n)n(n-k^{2})}}\sin \arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}\sin \phi _{1}\sin \phi _{2}}{{\frac {n\cos \phi _{1}\cos \phi _{2}-n\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}{\sqrt {1-k^{2}\sin ^{2}\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}}}\sin \phi _{1}\sin \phi _{2}+1-n\sin ^{2}\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aecc6843efc7125845fda08e45c077f981276566)
![{\displaystyle {\frac {\partial }{\partial n}}\Pi (n;\phi ,k)={\frac {1}{2(k^{2}-n)(n-1)}}\left[E(\phi ;k)+{\frac {(k^{2}-n)F(\phi ;k)}{n}}+{\frac {(n^{2}-k^{2})\Pi (n;\phi ,k)}{n}}-{\frac {n{\sqrt {1-k^{2}\sin \phi }}\sin 2\phi }{2(1-n\sin ^{2}\phi )}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ab1e3193951a021adf86192ac8b7ab379b43e9c)


![{\displaystyle {\frac {\partial }{\partial k}}\Pi (n;\phi ,k)={\frac {k}{n-k^{2}}}\left[{\frac {E(\phi ;k)}{k^{2}-1}}+\Pi (n;\phi ,k)-{\frac {k^{2}\sin 2\phi }{2(k^{2}-1){\sqrt {1-k^{2}\sin ^{2}\phi }}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b58449775f292c66d7806ecce70461760938d014)
![{\displaystyle \Pi (n;\phi ,1)={\frac {1}{2n-2}}\left[{\sqrt {n}}\ln {\frac {1+{\sqrt {n}}\sin \phi }{1-{\sqrt {n}}\sin \phi }}-2\ln(\sec \phi +\tan \phi )\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b67a073512a469f04ff3a6037960156f472458ba)




![{\displaystyle \Pi (n;\phi ,{\sqrt {n}})={\frac {1}{1-n}}\left[E(\phi ,{\sqrt {n}})-{\frac {n\sin 2\phi }{2{\sqrt {1-n\sin ^{2}\phi }}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada6fafca2f1c3b38ee137c2f4af985caa131373)


 第一类完全椭圆积分
第一类完全椭圆积分
如果幅度为 或者
或者 ,则称椭圆积分为完全的。
第一类完全椭圆积分
,则称椭圆积分为完全的。
第一类完全椭圆积分 可以定义为
可以定义为

或者

它是第一类不完全椭圆积分的特例:

这个特例可以表达为幂级数
![{\displaystyle K(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a1732c09b706f65010964c8eb2d138352b43b8)
它等价于
![{\displaystyle K(k)={\frac {\pi }{2}}\left\{1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\cdots +\left[{\frac {(2n-1)!!}{(2n)!!}}\right]^{2}k^{2n}+\cdots \right\}.\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adaa1415b97d76b4b2307931d732a47f6eab945d)
其中 表示双阶乘。利用高斯的超几何函数,第一类完全椭圆积分可以表达为
表示双阶乘。利用高斯的超几何函数,第一类完全椭圆积分可以表达为

第一类完全椭圆积分有时称为四分周期。它可以利用算术几何平均值来快速计算。

![{\displaystyle \Re \left[K(x+y{\rm {i}})\right]={\frac {\pi }{2}}F_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {3}{4}},{\frac {3}{4}},{\frac {5}{4}},{\frac {5}{4}},;;;\\1,{\frac {3}{2}};{\frac {1}{2}};{\frac {3}{2}};\\-y^{2},x^{2}\end{bmatrix}}+{\frac {\pi }{8}}xF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {1}{4}},{\frac {1}{4}},{\frac {3}{4}},{\frac {3}{4}},;;;\\1,{\frac {1}{2}};{\frac {1}{2}};{\frac {1}{2}};\\-y^{2},x^{2}\end{bmatrix}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd58076843e5f27fd7d415891a57016c2f17042)
![{\displaystyle \Im \left[K(x+y{\rm {i}})\right]={\frac {\pi }{8}}yF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {3}{4}},{\frac {5}{4}},{\frac {3}{4}},{\frac {5}{4}},;;;\\1,{\frac {3}{2}};{\frac {3}{2}};{\frac {1}{2}};\\-y^{2},x^{2}\end{bmatrix}}+{\frac {9}{64}}\pi xyF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {5}{4}},{\frac {7}{4}},{\frac {7}{4}},{\frac {5}{4}},;;;\\2,{\frac {3}{2}};{\frac {3}{2}};{\frac {3}{2}};\\-y^{2},x^{2}\end{bmatrix}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/509466b527c33780166165a209e68a8e591b8f6e)






![{\displaystyle K\left({\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{4}}\cdot {\sqrt[{4}]{3}}}{8\pi }}\Gamma ^{3}\left({\frac {1}{3}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c09f7f77ddcd5609827fc1a1c04170775892dccc)
![{\displaystyle K\left({\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{4}}\cdot {\sqrt[{4}]{27}}}{8\pi }}\Gamma ^{3}\left({\frac {1}{3}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc60d1b60385175f7231002c813ab3aaf347a3eb)



其中


第一类完全椭圆积分满足



这个近似在k<1/2时相对误差小于3×10−4,若只保留前两项则误差在k<1/2时小于0.01
此函数满足以下微分方程
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} k}}\left[k(1-k^{2}){\frac {\mathrm {d} K(k)}{\mathrm {d} k}}\right]=kK(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db809432b43a7c3f41a1e3de08ff3462a8d05eb0)
此微分方程之另一解为 ,此解满足以下关系。
,此解满足以下关系。
 .
.
 第二类完全椭圆积分
第二类完全椭圆积分
第二类完全椭圆积分  可以定义为
可以定义为

或者

它是第二类不完全椭圆积分的特殊情况:

它可以用幂级数表达
![{\displaystyle E(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}n!^{2}}}\right]^{2}{\frac {k^{2n}}{1-2n}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15647ca7df18b0ecfe518cbee10ac052684c74b5)
也就是
![{\displaystyle E(k)={\frac {\pi }{2}}\left\{1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\cdots -\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}{\frac {k^{2n}}{2n-1}}-\cdots \right\}.\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be312fce8bf5be9afd473420c32fee44f1eb48ec)
用高斯超几何函数表示的话,第二类完全椭圆积分可以写作

有如下性质











![{\displaystyle E\left({\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{2}}\cdot \ {\sqrt[{4}]{3}}}{3\Gamma ^{3}\left({\frac {1}{3}}\right)}}{\pi }^{2}+{\frac {{\sqrt[{3}]{4}}\left(3{\sqrt[{4}]{3}}+{\sqrt[{4}]{27}}\right)}{48{\pi }}}\Gamma ^{3}\left({\frac {1}{3}}\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e6cd80d6f2ab58725a63f6784b630a1e23c077)
![{\displaystyle E\left({\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{2}}\cdot \ {\sqrt[{4}]{27}}}{3\Gamma ^{3}\left({\frac {1}{3}}\right)}}{\pi }^{2}+{\frac {{\sqrt[{3}]{4}}\left({\sqrt[{4}]{27}}-{\sqrt[{4}]{3}}\right)}{16{\pi }}}\Gamma ^{3}\left({\frac {1}{3}}\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bba584ba1b826c86ba708a12245a090754fcb4)
![{\displaystyle E({\sqrt {2}}-1)={\frac {\sqrt {\pi }}{8}}\left[{\frac {\Gamma ({\frac {1}{8}})}{\Gamma ({\frac {5}{8}})}}+{\frac {\Gamma ({\frac {5}{8}})}{\Gamma ({\frac {9}{8}})}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4daf3feb49c5e32fe906961315e593f9b3216e83)

其中





![{\displaystyle \int E(k){\rm {d}}k={\frac {2}{3}}\left[kK(k)-K(k)+kE(k)+E(k)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c83e2aa59281b01e21f3f1ce2e41e8fb366c46c)
![{\displaystyle (k^{2}-1){\frac {\mathrm {d} }{\mathrm {d} k}}\left[k\;{\frac {\mathrm {d} E(k)}{\mathrm {d} k}}\right]=kE(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14259fc7b0318212f66c2b207276f8f26d5934e3)
此微分方程之另解为 。
。
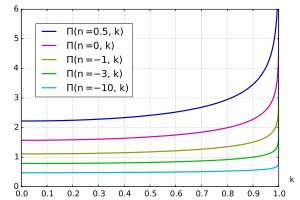 不同
不同 值的第三类完全椭圆积分
值的第三类完全椭圆积分
第三类完全椭圆积分 可以定义为
可以定义为

注意有时第三类椭圆积分被定义为带相反符号的 ,也即
,也即

用阿佩尔函数可表示为

第三类完全椭圆积分和第一类椭圆积分之间的关系
![{\displaystyle \Pi \left[{\frac {(1+x)(1-3x)}{(1-x)(1+3x)}},{\frac {(1+x)^{3}(1-3x)}{(1-x)^{3}(1+3x)}}\right]-{\frac {1+3x}{6x}}K\left[{\frac {(1+x)^{3}(1-3x)}{(1-x)^{3}(1+3x)}}\right]=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f193a723b1d1a29a9ebfa2efc6f5e8655c95d1c6)

如


![{\displaystyle {\frac {\partial }{\partial n}}\Pi (n,k)={\frac {1}{2(k^{2}-n)(n-1)}}\left[E(k)+{\frac {(k^{2}-n)K(k)}{n}}+{\frac {(n^{2}-k^{2})\Pi (n,k)}{n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ca439e8b50855b51c094d6c05244bb20ae21be5)
![{\displaystyle {\frac {\partial }{\partial k}}\Pi (n,k)={\frac {k}{n-k^{2}}}\left[{\frac {E(k)}{k^{2}-1}}+\Pi (n,k)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f31355f7b6bf211ba697b4c23f68fdbd1d918045)







勒让得关系指出了第一类和第二类完全椭圆积分之间的联系:






![{\displaystyle f(x)=\int _{c}^{x}R[t,{\sqrt[{}]{P(t)}}]\ dt\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64997726d1cd7063eddda9718a71431e3a23789)







![{\displaystyle F[{\textrm {sn}}\left(z;k\right);k]=z\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c66802524275339337594efabdd82b3dd6fb86)


























![{\displaystyle \forall \varphi _{1},\varphi _{2}\in \left]-{\frac {\pi }{2}};{\frac {\pi }{2}}\right[,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/989fec711a792ee800b77b31e2335eac09a567cf)

![{\displaystyle \arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\in [-\pi /2;\pi /2]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbce7940dbd301d450a8df8f9e5ec059be6184d5)

![{\displaystyle \arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\in [0;\pi ]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/847d9b225998e6ff4e6ba2417215602b7344d425)

















![{\displaystyle \textstyle E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42b85802f1d5c5d1662a33f4d575098caf657bd)












![{\displaystyle \Pi (n;\phi _{1},k)+\Pi (n;\phi _{2},k)=\Pi \left[n;\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}},k\right]-{\sqrt {\frac {n}{(1-n)(n-k^{2})}}}\arctan {\frac {{\sqrt {(1-n)n(n-k^{2})}}\sin \arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}\sin \phi _{1}\sin \phi _{2}}{{\frac {n\cos \phi _{1}\cos \phi _{2}-n\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}{\sqrt {1-k^{2}\sin ^{2}\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}}}\sin \phi _{1}\sin \phi _{2}+1-n\sin ^{2}\arccos {\frac {\cos \phi _{1}\cos \phi _{2}-\sin \phi _{1}\sin \phi _{2}{\sqrt {(1-k^{2}\sin ^{2}\phi _{1})(1-k^{2}\sin ^{2}\phi _{2})}}}{1-k^{2}\sin ^{2}\phi _{1}\sin ^{2}\phi _{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aecc6843efc7125845fda08e45c077f981276566)
![{\displaystyle {\frac {\partial }{\partial n}}\Pi (n;\phi ,k)={\frac {1}{2(k^{2}-n)(n-1)}}\left[E(\phi ;k)+{\frac {(k^{2}-n)F(\phi ;k)}{n}}+{\frac {(n^{2}-k^{2})\Pi (n;\phi ,k)}{n}}-{\frac {n{\sqrt {1-k^{2}\sin \phi }}\sin 2\phi }{2(1-n\sin ^{2}\phi )}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ab1e3193951a021adf86192ac8b7ab379b43e9c)


![{\displaystyle {\frac {\partial }{\partial k}}\Pi (n;\phi ,k)={\frac {k}{n-k^{2}}}\left[{\frac {E(\phi ;k)}{k^{2}-1}}+\Pi (n;\phi ,k)-{\frac {k^{2}\sin 2\phi }{2(k^{2}-1){\sqrt {1-k^{2}\sin ^{2}\phi }}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b58449775f292c66d7806ecce70461760938d014)
![{\displaystyle \Pi (n;\phi ,1)={\frac {1}{2n-2}}\left[{\sqrt {n}}\ln {\frac {1+{\sqrt {n}}\sin \phi }{1-{\sqrt {n}}\sin \phi }}-2\ln(\sec \phi +\tan \phi )\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b67a073512a469f04ff3a6037960156f472458ba)



![{\displaystyle \Pi (n;\phi ,{\sqrt {n}})={\frac {1}{1-n}}\left[E(\phi ,{\sqrt {n}})-{\frac {n\sin 2\phi }{2{\sqrt {1-n\sin ^{2}\phi }}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada6fafca2f1c3b38ee137c2f4af985caa131373)









![{\displaystyle K(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a1732c09b706f65010964c8eb2d138352b43b8)
![{\displaystyle K(k)={\frac {\pi }{2}}\left\{1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\cdots +\left[{\frac {(2n-1)!!}{(2n)!!}}\right]^{2}k^{2n}+\cdots \right\}.\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adaa1415b97d76b4b2307931d732a47f6eab945d)



![{\displaystyle \Re \left[K(x+y{\rm {i}})\right]={\frac {\pi }{2}}F_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {3}{4}},{\frac {3}{4}},{\frac {5}{4}},{\frac {5}{4}},;;;\\1,{\frac {3}{2}};{\frac {1}{2}};{\frac {3}{2}};\\-y^{2},x^{2}\end{bmatrix}}+{\frac {\pi }{8}}xF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {1}{4}},{\frac {1}{4}},{\frac {3}{4}},{\frac {3}{4}},;;;\\1,{\frac {1}{2}};{\frac {1}{2}};{\frac {1}{2}};\\-y^{2},x^{2}\end{bmatrix}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd58076843e5f27fd7d415891a57016c2f17042)
![{\displaystyle \Im \left[K(x+y{\rm {i}})\right]={\frac {\pi }{8}}yF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {3}{4}},{\frac {5}{4}},{\frac {3}{4}},{\frac {5}{4}},;;;\\1,{\frac {3}{2}};{\frac {3}{2}};{\frac {1}{2}};\\-y^{2},x^{2}\end{bmatrix}}+{\frac {9}{64}}\pi xyF_{2\times 1\times 1}^{4\times 0\times 0}{\begin{bmatrix}{\frac {5}{4}},{\frac {7}{4}},{\frac {7}{4}},{\frac {5}{4}},;;;\\2,{\frac {3}{2}};{\frac {3}{2}};{\frac {3}{2}};\\-y^{2},x^{2}\end{bmatrix}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/509466b527c33780166165a209e68a8e591b8f6e)






![{\displaystyle K\left({\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{4}}\cdot {\sqrt[{4}]{3}}}{8\pi }}\Gamma ^{3}\left({\frac {1}{3}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c09f7f77ddcd5609827fc1a1c04170775892dccc)
![{\displaystyle K\left({\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{4}}\cdot {\sqrt[{4}]{27}}}{8\pi }}\Gamma ^{3}\left({\frac {1}{3}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc60d1b60385175f7231002c813ab3aaf347a3eb)








![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} k}}\left[k(1-k^{2}){\frac {\mathrm {d} K(k)}{\mathrm {d} k}}\right]=kK(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db809432b43a7c3f41a1e3de08ff3462a8d05eb0)







![{\displaystyle E(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}n!^{2}}}\right]^{2}{\frac {k^{2n}}{1-2n}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15647ca7df18b0ecfe518cbee10ac052684c74b5)
![{\displaystyle E(k)={\frac {\pi }{2}}\left\{1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\cdots -\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}{\frac {k^{2n}}{2n-1}}-\cdots \right\}.\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be312fce8bf5be9afd473420c32fee44f1eb48ec)











![{\displaystyle E\left({\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{2}}\cdot \ {\sqrt[{4}]{3}}}{3\Gamma ^{3}\left({\frac {1}{3}}\right)}}{\pi }^{2}+{\frac {{\sqrt[{3}]{4}}\left(3{\sqrt[{4}]{3}}+{\sqrt[{4}]{27}}\right)}{48{\pi }}}\Gamma ^{3}\left({\frac {1}{3}}\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e6cd80d6f2ab58725a63f6784b630a1e23c077)
![{\displaystyle E\left({\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}\right)={\frac {{\sqrt[{3}]{2}}\cdot \ {\sqrt[{4}]{27}}}{3\Gamma ^{3}\left({\frac {1}{3}}\right)}}{\pi }^{2}+{\frac {{\sqrt[{3}]{4}}\left({\sqrt[{4}]{27}}-{\sqrt[{4}]{3}}\right)}{16{\pi }}}\Gamma ^{3}\left({\frac {1}{3}}\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bba584ba1b826c86ba708a12245a090754fcb4)
![{\displaystyle E({\sqrt {2}}-1)={\frac {\sqrt {\pi }}{8}}\left[{\frac {\Gamma ({\frac {1}{8}})}{\Gamma ({\frac {5}{8}})}}+{\frac {\Gamma ({\frac {5}{8}})}{\Gamma ({\frac {9}{8}})}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4daf3feb49c5e32fe906961315e593f9b3216e83)






![{\displaystyle \int E(k){\rm {d}}k={\frac {2}{3}}\left[kK(k)-K(k)+kE(k)+E(k)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c83e2aa59281b01e21f3f1ce2e41e8fb366c46c)
![{\displaystyle (k^{2}-1){\frac {\mathrm {d} }{\mathrm {d} k}}\left[k\;{\frac {\mathrm {d} E(k)}{\mathrm {d} k}}\right]=kE(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14259fc7b0318212f66c2b207276f8f26d5934e3)







![{\displaystyle \Pi \left[{\frac {(1+x)(1-3x)}{(1-x)(1+3x)}},{\frac {(1+x)^{3}(1-3x)}{(1-x)^{3}(1+3x)}}\right]-{\frac {1+3x}{6x}}K\left[{\frac {(1+x)^{3}(1-3x)}{(1-x)^{3}(1+3x)}}\right]=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f193a723b1d1a29a9ebfa2efc6f5e8655c95d1c6)



![{\displaystyle {\frac {\partial }{\partial n}}\Pi (n,k)={\frac {1}{2(k^{2}-n)(n-1)}}\left[E(k)+{\frac {(k^{2}-n)K(k)}{n}}+{\frac {(n^{2}-k^{2})\Pi (n,k)}{n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ca439e8b50855b51c094d6c05244bb20ae21be5)
![{\displaystyle {\frac {\partial }{\partial k}}\Pi (n,k)={\frac {k}{n-k^{2}}}\left[{\frac {E(k)}{k^{2}-1}}+\Pi (n,k)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f31355f7b6bf211ba697b4c23f68fdbd1d918045)







