本文只考虑欧几里得空间中的曲线。大部分概念对
黎曼 与
伪黎曼 流形 中曲线有类似结论。对任意
空间 中曲线的讨论,参见主条目
曲线 。
曲线的微分几何 是几何学 的一个分支,使用微分 与积分 专门研究平面 与欧几里得空间 中的光滑 曲线 。
从古代开始,许多具体曲线 已经用综合方法深入研究。微分几何 采取另外一种方式:把曲线表示为参数形式 ,将它们的几何性质和各种量,比如曲率 和弧长 ,用向量分析 表示为导数 和积分 。分析曲线最重要的工具之一为 Frenet 标架 ,是一个活动标架 ,在曲线每一点附近给出“最合适”的坐标系。
曲线的理论比曲面理论 及其高维推广的范围要狭窄得多,也简单得多。因为欧几里得空间中的正则曲线没有内蕴几何。任何正则曲线可以用弧长(“自然参数”)参数化,从曲线上来看不能知道周围空间的任何信息,所有曲线都是一样的。不同空间曲线只是由它们的弯曲和扭曲程度区分。数量上,这由微分几何不变量曲线的“曲率 ”和“挠率 ”来衡量。曲线基本定理 断言这些不变量的信息完全确定了曲线。
设
n
{\displaystyle n}
r
{\displaystyle r}
∞
{\displaystyle \infty }
I
{\displaystyle I}
非空 区间,
t
{\displaystyle t}
I
{\displaystyle I}
C
r
{\displaystyle C^{r}}
γ
{\displaystyle \gamma }
r
{\displaystyle r}
连续可微 )向量值函数
γ
:
I
→
R
n
{\displaystyle \mathbf {\gamma } :I\to {\mathbb {R} }^{n}}
称为一条
C
r
{\displaystyle C^{r}}
γ
{\displaystyle \gamma }
C
r
{\displaystyle C^{r}}
t
{\displaystyle t}
γ
{\displaystyle \gamma }
γ
(
I
)
{\displaystyle \gamma (I)}
像 。将参数曲线
γ
{\displaystyle \gamma }
γ
(
I
)
{\displaystyle \gamma (I)}
R
n
{\displaystyle {\mathbb {R} }^{n}}
可以想象参数
t
{\displaystyle t}
γ
(
t
)
{\displaystyle \gamma (t)}
轨迹 。
如果 I 是闭区间 [a , b ],我们称 γ(a ) 为曲线 γ 的起点 而 γ(b ) 为终点 。
如果
γ
(
a
)
=
γ
(
b
)
{\displaystyle \gamma (a)=\gamma (b)}
闭的 或是一个环路 。进一步,我们称 γ 是一条闭 Cr -曲线 ,如果 γ(k ) (a) = γ(k ) (b ) 对所有 k ≤ r 。
如果
γ
:
(
a
,
b
)
→
R
n
{\displaystyle \gamma :(a,b)\to \mathbb {R} ^{n}}
单射 ,我们称为简单 曲线。
如果参数曲线
γ
{\displaystyle \gamma }
幂级数 ,我们称曲线解析 或是
C
ω
{\displaystyle C^{\omega }}
记号 -
γ
{\displaystyle \gamma }
一条
C
k
{\displaystyle C^{k}}
γ
:
[
a
,
b
]
→
R
n
{\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}
称为
m
{\displaystyle m}
当且仅当 对任何
t
{\displaystyle t}
I
{\displaystyle I}
{
γ
′
(
t
)
,
γ
″
(
t
)
,
.
.
.
,
γ
(
m
)
(
t
)
}
,
m
≤
k
{\displaystyle \lbrace \gamma '(t),\gamma ''(t),...,\gamma ^{(m)}(t)\rbrace {\mbox{, }}m\leq k}
在
R
n
{\displaystyle \mathbb {R} ^{n}}
线性无关 。
特别地,一条
C
1
{\displaystyle C^{1}}
γ
{\displaystyle \gamma }
正则 的如果
γ
′
(
t
)
≠
0
{\displaystyle \gamma '(t)\neq 0}
t
∈
I
.
{\displaystyle t\in I\,.}
给定一条曲线的像我们可以定义曲线的许多不同的参数化。微分几何旨在描述在一定的参数化下不变的性质。所以我们需在所有参数曲线集合上定义一种合适的等价关系 。曲线的微分几何性质(长度,Frenet 标架 和广义曲率)在重新参数化下不变从而满足等价类 性质。这个等价类称为 Cr 曲线 ,是曲线的微分几何研究的中心。
两个 C r
γ
1
:
I
1
→
R
n
{\displaystyle \mathbf {\gamma _{1}} :I_{1}\to R^{n}}
与
γ
2
:
I
2
→
R
n
{\displaystyle \mathbf {\gamma _{2}} :I_{2}\to R^{n}}
要称为等价 ,就要存在一个 C r 双射
ϕ
:
I
1
→
I
2
{\displaystyle \phi :I_{1}\to I_{2}}
使得
ϕ
′
(
t
)
≠
0
(
t
∈
I
1
)
{\displaystyle \phi '(t)\neq 0\qquad (t\in I_{1})}
和
γ
2
(
ϕ
(
t
)
)
=
γ
1
(
t
)
(
t
∈
I
1
)
.
{\displaystyle \mathbf {\gamma _{2}} (\phi (t))=\mathbf {\gamma _{1}} (t)\qquad (t\in I_{1})\,.}
γ2 称为 γ1 的重新参数化 。这种 γ1 的重新参数化在所有参数 C r Cr 曲线 。
对定向 Cr 曲线 ,我们可以定义一种“加细”的等价关系,要求 φ 满足 φ'(t ) > 0。
等价的 C r C r
C 1 曲线 γ : [a , b ] → R n l 可以定义为
l
=
∫
a
b
|
γ
′
(
t
)
|
d
t
.
{\displaystyle l=\int _{a}^{b}\vert \mathbf {\gamma } '(t)\vert dt.}
曲线的长度在重参数化下保持不变,从而是曲线的一个微分几何性质。
对任何正则 C r r 至少为 1)曲线 γ: [a , b ] → R n
s
(
t
)
=
∫
t
0
t
|
γ
′
(
x
)
|
d
x
.
{\displaystyle s(t)=\int _{t_{0}}^{t}\vert \mathbf {\gamma } '(x)\vert dx.}
写成
γ
(
s
)
¯
=
γ
(
t
(
s
)
)
{\displaystyle {\overline {\mathbf {\gamma } (s)}}=\gamma (t(s))}
这里 t (s ) 是 s (t ) 的逆函数,我们得到 γ 的一个新参数化
γ
¯
{\displaystyle {\bar {\gamma }}}
自然 、弧长 或单位速度 参数化;参数 s (t ) 称为 γ 的自然参数 。
我们偏爱这个参数,因为自然参数 s (t ) 以单位速度转动 γ 的像,所以
|
γ
′
(
s
(
t
)
)
¯
|
=
1
(
t
∈
I
)
.
{\displaystyle \vert {\overline {\mathbf {\gamma } '(s(t))}}\vert =1\qquad (t\in I).}
在实际中常常很难计算出一条曲线的自然参数,但在理论讨论中很有用。
给定一条参数化曲线 γ(t ) 的自然参数化是在差一个参数移动的意义下是惟一的。
数量
E
(
γ
)
=
1
2
∫
a
b
|
γ
′
(
t
)
|
2
d
t
{\displaystyle E(\gamma )={\frac {1}{2}}\int _{a}^{b}\vert \mathbf {\gamma } '(t)\vert ^{2}dt}
经常称为曲线的能量 或作用量 ;这个名称是有理由的,因为测地线 方程是这个作用量的欧拉-拉格朗日 运动方程。
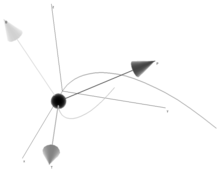
空间曲线一点的 Frenet 标架示意图。 T 是单位切向量,P 为单位法向量,B 是次法向量。 一个 Frenet 标架 是一个移动的参考标架 ,由描述曲线在每一点 γ(t ) 局部性质的n 个正交 向量 e i t ) 组成。这是微分几何处理曲线的主要工具,因为在这个局部参考系中,远比使用欧几里得那样的整体坐标系更容易和自然地描述局部性质(如曲率、挠率)。
给定 R n n 阶正则 C n +1Frenet 标架 是一组正交向量
e
1
(
t
)
,
…
,
e
n
(
t
)
{\displaystyle \mathbf {e} _{1}(t),\ldots ,\mathbf {e} _{n}(t)}
称为 Frenet 向量 t ) 的各阶导数使用格拉姆-施密特正交化算法 得到的:
e
1
(
t
)
=
γ
′
(
t
)
‖
γ
′
(
t
)
‖
{\displaystyle \mathbf {e} _{1}(t)={\frac {\mathbf {\gamma } '(t)}{\|\mathbf {\gamma } '(t)\|}}}
e
j
(
t
)
=
e
j
¯
(
t
)
‖
e
j
¯
(
t
)
‖
,
e
j
¯
(
t
)
=
γ
(
j
)
(
t
)
−
∑
i
=
1
j
−
1
⟨
γ
(
j
)
(
t
)
,
e
i
(
t
)
⟩
e
i
(
t
)
{\displaystyle \mathbf {e} _{j}(t)={\frac {{\overline {\mathbf {e} _{j}}}(t)}{\|{\overline {\mathbf {e} _{j}}}(t)\|}}{\mbox{, }}{\overline {\mathbf {e} _{j}}}(t)=\mathbf {\gamma } ^{(j)}(t)-\sum _{i=1}^{j-1}\langle \mathbf {\gamma } ^{(j)}(t),\mathbf {e} _{i}(t)\rangle \,\mathbf {e} _{i}(t)}
实值函数 χi t ) 称为 广义曲率 ,定义为
χ
i
(
t
)
=
⟨
e
i
′
(
t
)
,
e
i
+
1
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \chi _{i}(t)={\frac {\langle \mathbf {e} _{i}'(t),\mathbf {e} _{i+1}(t)\rangle }{\|\mathbf {\gamma } ^{'}(t)\|}}}
Frenet 标架和广义曲率在重新参数化下是不变的,故它们是曲线的微分几何性质。
最初三个 Frenet 向量和广义曲率可以在三维空间中看到。它们有额外的名字以及与名称相关更多信息。
如果曲线 γ 表示一个质点的轨迹,那么质点在给定点 P 的瞬时速度用一个向量 表示,称为曲线在 P 的切向量 。
数学表述为,给定一条曲线 γ = γ(t ),对参数 t 的任何值: t = t0 ,
向量:
γ
′
(
t
0
)
=
d
d
t
γ
(
t
)
,
t
=
t
0
{\displaystyle \gamma '(t_{0})={\frac {d}{d\,t}}\mathbf {\gamma } (t),{t=t_{0}}}
是点 P = γ(t0 ) 的切向量。一般说,切向量可以为零向量 。
切向量的长度:
‖
γ
′
(
t
0
)
‖
{\displaystyle \|\mathbf {\gamma } '(t_{0})\|}
是在时间 t 0 的速率。
e1 (t ) 是在同一方向的单位切向量 ,在 γ 的每个正则点有定义:
e
1
(
t
)
=
γ
′
(
t
)
‖
γ
′
(
t
)
‖
.
{\displaystyle \mathbf {e} _{1}(t)={\frac {\mathbf {\gamma } '(t)}{\|\mathbf {\gamma } '(t)\|}}.}
如果 t = s 是自然参数则切向量有单位长,从而公式化简为:
e
1
(
s
)
=
γ
′
(
s
)
.
{\displaystyle \mathbf {e} _{1}(s)=\mathbf {\gamma } '(s).}
单位切向量确定了曲线的定向 ,或随著参数增长的前进方向。
法向量 ,有时也称为曲率向量 ,表明曲线和一条直线的偏离程度。
法向量定义为
e
2
¯
(
t
)
=
γ
″
(
t
)
−
⟨
γ
″
(
t
)
,
e
1
(
t
)
⟩
e
1
(
t
)
.
{\displaystyle {\overline {\mathbf {e} _{2}}}(t)=\mathbf {\gamma } ''(t)-\langle \mathbf {\gamma } ''(t),\mathbf {e} _{1}(t)\rangle \,\mathbf {e} _{1}(t).}
其正规形式单位法向量 ,是 Frenet 向量 e 2 (t ),定义为
e
2
(
t
)
=
e
2
¯
(
t
)
‖
e
2
¯
(
t
)
‖
.
{\displaystyle \mathbf {e} _{2}(t)={\frac {{\overline {\mathbf {e} _{2}}}(t)}{\|{\overline {\mathbf {e} _{2}}}(t)\|}}.}
t 点的切向量和法向量张成 t 点的密切平面 。
第一个广义曲率 χ1 (t ) 称为曲率 ,度量了曲线 γ 偏离密切平面上一条直线的程度。定义为
κ
(
t
)
=
χ
1
(
t
)
=
⟨
e
1
′
(
t
)
,
e
2
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \kappa (t)=\chi _{1}(t)={\frac {\langle \mathbf {e} _{1}'(t),\mathbf {e} _{2}(t)\rangle }{\|\mathbf {\gamma } ^{'}(t)\|}}}
称为 γ 在点 t 的曲率 。
曲率的倒数
1
κ
(
t
)
{\displaystyle {\frac {1}{\kappa (t)}}}
称为曲率半径 。
半径为 r 的圆周有常曲率
κ
(
t
)
=
1
r
,
{\displaystyle \kappa (t)={\frac {1}{r}}\,,}
但一条直线的曲率是 0 。
次法向量 是第三个 Frenet 向量 e 3 (t ) ,
总是正交于 t 点的单位 切向量和单位法向量。其定义为
e
3
(
t
)
=
e
3
¯
(
t
)
‖
e
3
¯
(
t
)
‖
e
3
¯
(
t
)
=
γ
‴
(
t
)
−
⟨
γ
‴
(
t
)
,
e
1
(
t
)
⟩
e
1
(
t
)
−
⟨
γ
‴
(
t
)
,
e
2
(
t
)
⟩
e
2
(
t
)
{\displaystyle \mathbf {e} _{3}(t)={\frac {{\overline {\mathbf {e} _{3}}}(t)}{\|{\overline {\mathbf {e} _{3}}}(t)\|}}\quad {\overline {\mathbf {e} _{3}}}(t)=\mathbf {\gamma } '''(t)-\langle \mathbf {\gamma } '''(t),\mathbf {e} _{1}(t)\rangle \,\mathbf {e} _{1}(t)-\langle \mathbf {\gamma } '''(t),\mathbf {e} _{2}(t)\rangle \,\mathbf {e} _{2}(t)}
在 3 维空间中等式简化为
e
3
(
t
)
=
e
2
(
t
)
×
e
1
(
t
)
.
{\displaystyle \mathbf {e} _{3}(t)=\mathbf {e} _{2}(t)\times \mathbf {e} _{1}(t)\,.}
第二广义曲率 χ2 (t ) 称为挠率 ,度量了 γ 和一条平面曲线的偏离程度。或者说,如果挠率为 0 则曲线完全在某平面内(任何 t 都在这一个平面内)。
τ
(
t
)
=
χ
2
(
t
)
=
⟨
e
2
′
(
t
)
,
e
3
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \tau (t)=\chi _{2}(t)={\frac {\langle \mathbf {e} _{2}'(t),\mathbf {e} _{3}(t)\rangle }{\|\mathbf {\gamma } '(t)\|}}}
称为 γ 在点 t 的挠率 。
给定 n 个函数
χ
i
∈
C
n
−
i
(
[
a
,
b
]
)
,
1
≤
i
≤
n
{\displaystyle \chi _{i}\in C^{n-i}([a,b]){\mbox{, }}1\leq i\leq n}
满足
χ
i
(
t
)
>
0
,
1
≤
i
≤
n
−
1
{\displaystyle \chi _{i}(t)>0{\mbox{, }}1\leq i\leq n-1}
那么存在惟一的 (在差一个欧几里得群 作用的意义下) n 阶正则 C n +1
‖
γ
′
(
t
)
‖
=
1
(
t
∈
[
a
,
b
]
)
{\displaystyle \|\gamma '(t)\|=1{\mbox{ }}(t\in [a,b])}
χ
i
(
t
)
=
⟨
e
i
′
(
t
)
,
e
i
+
1
(
t
)
⟩
‖
γ
′
(
t
)
‖
,
{\displaystyle \chi _{i}(t)={\frac {\langle \mathbf {e} _{i}'(t),\mathbf {e} _{i+1}(t)\rangle }{\|\mathbf {\gamma } '(t)\|}}\,,}
这里集合
e
1
(
t
)
,
…
,
e
n
(
t
)
{\displaystyle \mathbf {e} _{1}(t),\ldots ,\mathbf {e} _{n}(t)}
是曲面的 Frenet 标架。
再附加起始 t 0 ∈ I ,起始点 p 0 ∈ R n e 1 , ..., e n -1
γ
(
t
0
)
=
p
0
{\displaystyle \mathbf {\gamma } (t_{0})=\mathbf {p} _{0}}
e
i
(
t
0
)
=
e
i
,
1
≤
i
≤
n
−
1
{\displaystyle \mathbf {e} _{i}(t_{0})=\mathbf {e} _{i}{\mbox{, }}1\leq i\leq n-1}
那么我们可以排除欧几里得作用得到惟一的曲线 γ。
Frenet-Serret 公式是一组一阶常微分方程 。其解为由广义曲率函数 χi
[
e
1
′
(
t
)
e
2
′
(
t
)
]
=
[
0
κ
(
t
)
−
κ
(
t
)
0
]
[
e
1
(
t
)
e
2
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\mathbf {e} _{2}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\kappa (t)\\-\kappa (t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\mathbf {e} _{2}(t)\\\end{bmatrix}}}
[
e
1
′
(
t
)
e
2
′
(
t
)
e
3
′
(
t
)
]
=
[
0
κ
(
t
)
0
−
κ
(
t
)
0
τ
(
t
)
0
−
τ
(
t
)
0
]
[
e
1
(
t
)
e
2
(
t
)
e
3
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\mathbf {e} _{2}'(t)\\\mathbf {e} _{3}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\kappa (t)&0\\-\kappa (t)&0&\tau (t)\\0&-\tau (t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\mathbf {e} _{2}(t)\\\mathbf {e} _{3}(t)\\\end{bmatrix}}}
[
e
1
′
(
t
)
⋮
e
n
′
(
t
)
]
=
[
0
χ
1
(
t
)
0
−
χ
1
(
t
)
⋱
⋱
⋱
0
χ
n
−
1
(
t
)
0
−
χ
n
−
1
(
t
)
0
]
[
e
1
(
t
)
⋮
e
n
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\vdots \\\mathbf {e} _{n}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\chi _{1}(t)&&0\\-\chi _{1}(t)&\ddots &\ddots &\\&\ddots &0&\chi _{n-1}(t)\\0&&-\chi _{n-1}(t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\vdots \\\mathbf {e} _{n}(t)\\\end{bmatrix}}}
Erwin Kreyszig, Differential Geometry , Dover Publications, New York, 1991, ISBN 9780484667218 . Chapter II is is a classical treatment of Theory of Curves in 3-dimensions.
陈维桓,微分几何,北京大学出版社,北京,2006年,ISBN 7-301-10709.
















![{\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e103c376cd9ea50b5c12c8f5398ded4d2a3577)

































![{\displaystyle \chi _{i}\in C^{n-i}([a,b]){\mbox{, }}1\leq i\leq n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccea8628d1a310cfb40f69917da1a4124b60fcc7)

![{\displaystyle \|\gamma '(t)\|=1{\mbox{ }}(t\in [a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f0d59be10764f3c9481cb70324bfdb72331222)





