五十九种二十面体
外观

《五十九种二十面体》(英语:The Fifty-Nine Icosahedra)是一本由哈罗德·斯科特·麦克唐纳·考克斯特、帕特里克·杜·瓦尔、H·T·夫雷勒和J·F·皮特里撰写的主题为星形二十面体的数学书籍,书中依据杰弗里·查尔斯·珀西·米勒提出的一组规则列出并介绍一些与柏拉图正二十面体及相关凸正图形有关连的星形多面体[1][2]。
这本书最早由多伦多大学于1938年出版[1],第二版由施普林格出版社发行,随后于1982年K和D·克内尤以相同文字重新排版、绘图增加图表和新的参考资料和照片,并修订为塔奎的第三版[3],于1999年出版。
作者的贡献
[编辑]米勒的规则
[编辑]虽然米勒对这本书没有直接的贡献,但他与考克斯特和皮特里是往来密切的同事。他的贡献是他提出一套规则能从无限多种星形多面体中明确的定义出那些星形多面体是“重要且特别”的[1]:
- 多面体的面必须位于二十面体骨架内,即,不能超出正二十面体的边界外[4]。
- 构成这个多面体的所有面都必须视同一种形状,但是他们可以是断开的[5]。
- 构成面的所有部分都必须要属于三角对称群,没有则需要反射对称。这确保了组成的多面体属于二十面体对称[6]。
- 每个面上的每一条边都要与其他面的某条边接在一起,并构成一个无缝隙的立体[7]。
- 我们从考虑把元素可以分为两个集合的案例排除,使得每一个立体尽可能有完全图又兼具对称性[8]。
考克斯特
[编辑]考克斯特是推动本书完成的主要力量。他将已知的资料用一些方法比如组合数学和抽象的图论以及当时被用在小说中的几何环境以米勒的规则为基础进行分析。
他观察星座图的许多线段,然后设计出了一个演算法来以米勒的规则控制相邻平面区域的组合,来列举出所有符合米勒规则的星形二十面体组合[9]。
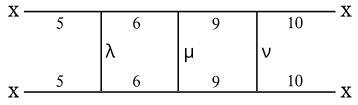
他绘制的图显示了个个确定连通的面。不同希腊字母代表可以替换的部分:
- λ 可能为 3 或 4
- μ 可能为 7 或 8
- ν 可能为 11 或 12
派屈克·杜·瓦尔
[编辑]帕特里克·杜·瓦尔借由观察各种星形二十面体位于“壳”的周围的原始二十面体而设计了一种适合表达星形二十面体各个胞的符号表示法。并在这个基础上测试米勒的规则可得到的所有可能的组合,并更加确定了考克斯特所使用的分析方法结果。
参见
[编辑]- 温尼尔二十面体模型列表 – 温尼尔的书 《多面体模型》中收录了21种星形二十面体
- 二十面体对称的多面体列表
- 星形二十面体列表
参考文献
[编辑]- ^ 1.0 1.1 1.2 Guy's. Stellation and facetting - a brief history. steelpillow.com. 2010-12-19 [2016-03-26]. (原始内容存档于2016-03-04).
- ^ Hart, G. "59 Stellations of the Icosahedron.". [2016-03-12]. (原始内容存档于2020-01-22).
- ^ Allanson, B. "The Fifty-Nine Icosahedra.". [2016-03-25]. (原始内容存档于2019-12-28).
- ^ polygons and polyhedra : paul scott : 59 stellations of the icosahedron I. paulscottinfo.ipage.com. [2016-03-25]. (原始内容存档于2019-12-27).
- ^ Stellation of Polyhedra. maplesoft.com. [2020-12-15]. (原始内容存档于2020-10-25).
- ^ H. S. M. Coxeter, P. Du Val, H. T. Flather, J. F. Petrie. The Fifty-Nine Icosahedra. SpringerLink. [2018-04-02]. doi:10.1007/978-1-4613-8216-4 (英国英语).
- ^ Ha Le. Stellation Process. Centre for Experimental and Constructive Mathematics. 1998-11-17 [2016-03-26]. (原始内容存档于2019-09-08).
- ^ Robert Webb. Stella Polyhedral Glossary. software3d.com. [2016-03-25]. (原始内容存档于2020-10-23).
- ^ Coxeter, H. S. M.; Du Val, P.; Flather, H. T.; and Petrie, J. F. The Fifty-Nine Icosahedra. Stradbroke, England: Tarquin Publications, 1999.
- Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte. Leipzig: B.G. Treubner. ISBN 978-1-4181-6590-1. (德文)
- WorldCat(页面存档备份,存于互联网档案馆) English: Polygons and Polyhedra: Theory and History. Photographs of models: Tafel VIII (Plate VIII), etc. High res. scans.(页面存档备份,存于互联网档案馆)
- H. S. M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26.
- Third edition (1999) Tarquin ISBN 978-1-899618-32-3 MR676126
- Wenninger, Magnus J. (1983) Polyhedron models; Cambridge University Press, Paperback edition (2003). ISBN 978-0-521-09859-5.
- A. H. Wheeler (1924) "Certain forms of the icosahedron and a method for deriving and designating higher polyhedra", Proceedings of the International Congress of Mathematicians, Toronto, Vol. 1, pp 701–708.
