白银比例| 白银比例 |
|---|
|

白银矩形 |
|
| 名称 | 白银比
白银分割比 |
|---|
|
| 种类 | 无理数 |
|---|
| 符号 |  |
|---|
| 位数数列编号 |  A014176 A014176 |
|---|
|
| 连分数 |  |
|---|
| 以此为根的多项式或函数 |  |
|---|
|
| 值 |  2.41421356... 2.41421356... |
|---|
| 代数形式 |  |
|---|
|
| 二进制 | 10.011010100000100111100110… |
|---|
| 十进制 | 2.414213562373095048801688… |
|---|
| 十六进制 | 2.6A09E667F3BCC908B2FB1366… |
|---|
|
|
|
白银分割率是一个无理数的数学常数,符号δS,定义为以下的数值:

又称白银比例、白银分割,白银比例的命名和黄金比例类似,斐波那契数列后一项和前一项的比值会趋近黄金比例,而佩尔数数列后一项和前一项的比值会趋近白银比例。白银比例和2的算术平方根、三角平方数、佩尔数及正八边形都有关系,希腊时期的数学家就已开始研究白银分割率,但当时没有为此一数值命名。
若二个数 和
和 的比值等于白银比,则二数可以满足以下的方程:
的比值等于白银比,则二数可以满足以下的方程:

白银比例可以用连续分数[2; 2, 2, 2, ...]表示

连续分数的渐近分数 即为连续二项佩尔数的比值。这些分数可提供白银分割率的准确丢番图逼近,就像连续二项斐波那契数列的比值可作为黄金比例的丢番图逼近一様。白银比例即第2贵金属分割。
即为连续二项佩尔数的比值。这些分数可提供白银分割率的准确丢番图逼近,就像连续二项斐波那契数列的比值可作为黄金比例的丢番图逼近一様。白银比例即第2贵金属分割。
白银比例的共轭数 其绝对值小于1,因此白银比例为皮索特-维贾亚拉加文数(PV数),且白银比例是第二小的二次PV数(最小的是黄金比例)。白银分割的乘幂距最接近整数的距离为
其绝对值小于1,因此白银比例为皮索特-维贾亚拉加文数(PV数),且白银比例是第二小的二次PV数(最小的是黄金比例)。白银分割的乘幂距最接近整数的距离为 ,会趋近于0。
,会趋近于0。
以下列出白银比例的几个乘幂:
![{\displaystyle \!\ \delta _{S}^{0}=[1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28afdcfd1d2162e4d1c8916954483e60414aa9e3)
![{\displaystyle \delta _{S}^{1}=\delta _{S}+0=[2;2,2,2,2,2,\dots ]\approx 2.41421}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da22da67490800e2358de670891d6f1a62824c5)
![{\displaystyle \delta _{S}^{2}=2\delta _{S}+1=[5;1,4,1,4,1,\dots ]\approx 5.82842}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f21030c1b14c77c31ad8abb6aacd680e678fbbac)
![{\displaystyle \delta _{S}^{3}=5\delta _{S}+2=[14;14,14,14,\dots ]\approx 14.07107}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a027dc6a0219d4911b34b55f89eb6be29eb4a01)
![{\displaystyle \delta _{S}^{4}=12\delta _{S}+5=[33;1,32,1,32,\dots ]\approx 33.97056}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8048daeeaf27de5d7ca01933e4f756099aec1e2)
乘幂的递回关系式如下:

其中

因此可用上式得到以下乘幂的值:
![{\displaystyle \!\ \delta _{S}^{5}=29\delta _{S}+12=[82;82,82,82,\dots ]\approx 82.01219}](https://wikimedia.org/api/rest_v1/media/math/render/svg/771bb96fcc4b522bd3f26f388524910970fa33bc)
利用 及
及  为初始条件,可以利用求解以下的递回关系式得到
为初始条件,可以利用求解以下的递回关系式得到 的解:
的解:

 可以表示为以下的式子
可以表示为以下的式子

白银比例和 的三角函数数值有关:
的三角函数数值有关:




边长为a的正八边形面积可以用下式表示:

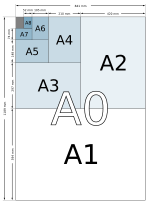
依ISO 216的纸张尺寸其长宽之间的比例为 ,若其中切掉一块边长和长方形短边相同的正方形,剩下的长方形长宽比例为
,若其中切掉一块边长和长方形短边相同的正方形,剩下的长方形长宽比例为 ,也等于
,也等于 ,此比例和白银比例有关。若一长方形的纵横比为白银比例,此长方形有时会称为“白银长方形”,不过白银长方形也可以指纵横比为√2的长方形。
,此比例和白银比例有关。若一长方形的纵横比为白银比例,此长方形有时会称为“白银长方形”,不过白银长方形也可以指纵横比为√2的长方形。

若将白银长方形切掉一块边长和长方形短边相同的正方形,剩下的会是白银长方形,再重复此步骤一次,会得到原来那一种白银长方形,但其比例为原来的 倍[1]。
倍[1]。
不过只有纵横比为 的长方形,其对半切开后可以得到二个纵横比例也是
的长方形,其对半切开后可以得到二个纵横比例也是 的较小长方形。
的较小长方形。
白银分割和正八边形有关,若正八边形分成二个相同大小的等腰梯形及一个长方形,则长方形的纵横比恰为白银比例,且梯形的四边比例会是 。
。
若正八边形的边长为t,则其内切圆的直径为 ,则面积为
,则面积为 .[1]。
.[1]。
























![{\displaystyle \!\ \delta _{S}^{0}=[1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28afdcfd1d2162e4d1c8916954483e60414aa9e3)
![{\displaystyle \delta _{S}^{1}=\delta _{S}+0=[2;2,2,2,2,2,\dots ]\approx 2.41421}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da22da67490800e2358de670891d6f1a62824c5)
![{\displaystyle \delta _{S}^{2}=2\delta _{S}+1=[5;1,4,1,4,1,\dots ]\approx 5.82842}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f21030c1b14c77c31ad8abb6aacd680e678fbbac)
![{\displaystyle \delta _{S}^{3}=5\delta _{S}+2=[14;14,14,14,\dots ]\approx 14.07107}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a027dc6a0219d4911b34b55f89eb6be29eb4a01)
![{\displaystyle \delta _{S}^{4}=12\delta _{S}+5=[33;1,32,1,32,\dots ]\approx 33.97056}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8048daeeaf27de5d7ca01933e4f756099aec1e2)


![{\displaystyle \!\ \delta _{S}^{5}=29\delta _{S}+12=[82;82,82,82,\dots ]\approx 82.01219}](https://wikimedia.org/api/rest_v1/media/math/render/svg/771bb96fcc4b522bd3f26f388524910970fa33bc)





















