在数学中,斯特林数 用于解决各种数学分析 和组合数学 问题,斯特林数是两组不同的数,均是18世纪由詹姆斯·斯特林 第一类斯特林数 第二类斯特林数 拉赫数 [ 1]
第一类斯特林数 递降阶乘 展开式的各项系数,即
(
x
)
n
=
∑
k
=
0
n
s
(
n
,
k
)
x
k
{\displaystyle (x)_{n}=\sum _{k=0}^{n}s(n,k)x^{k}\,}
s
(
n
,
k
)
{\displaystyle s(n,k)\,}
0
≤
k
≤
n
{\displaystyle 0\leq k\leq n\,}
(
x
)
3
=
x
(
x
−
1
)
(
x
−
2
)
{\displaystyle (x)_{3}=x(x-1)(x-2)\,}
则
(
x
)
3
=
0
⋅
x
0
+
2
⋅
x
−
3
⋅
x
2
+
1
⋅
x
3
{\displaystyle (x)_{3}=0\cdot x^{0}+2\cdot x-3\cdot x^{2}+1\cdot x^{3}\,}
于是
s
(
3
,
0
)
=
0
{\displaystyle s(3,0)=0\,}
s
(
3
,
1
)
=
2
{\displaystyle s(3,1)=2\,}
s
(
3
,
2
)
=
−
3
{\displaystyle s(3,2)=-3\,}
s
(
3
,
3
)
=
1
{\displaystyle s(3,3)=1\,}
由此可知,
s
(
n
,
k
)
{\displaystyle s(n,k)\,}
代数数 ,或称为有符号(第一类)斯特林数(英语:signed Stirling numbers of the first kind)。
有符号斯特林数的绝对值
|
s
(
n
,
k
)
|
{\displaystyle |s(n,k)|\,}
n
{\displaystyle n\,}
k
{\displaystyle k\,}
|
s
(
n
,
k
)
|
{\displaystyle |s(n,k)|\,}
算术数 ,或称为无符号(第一类)斯特林数(英语:unsigned Stirling numbers of the first kind)。无符号斯特林数一般可以记为
c
(
n
,
k
)
{\displaystyle c(n,k)\,}
[
n
k
]
{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
1
{\displaystyle 1\,}
2
{\displaystyle 2\,}
3
{\displaystyle 3\,}
0
{\displaystyle 0\,}
1
{\displaystyle 1\,}
(
1
2
3
)
{\displaystyle \left({\begin{matrix}&1&\\2&&3\end{matrix}}\right)\,}
(
1
3
2
)
{\displaystyle \left({\begin{matrix}&1&\\3&&2\end{matrix}}\right)\,}
2
{\displaystyle 2\,}
(
1
)
{\displaystyle \left({\begin{matrix}1\end{matrix}}\right)\,}
(
2
3
)
{\displaystyle \left({\begin{matrix}2&3\end{matrix}}\right)\,}
(
1
2
)
{\displaystyle \left({\begin{matrix}1&2\end{matrix}}\right)\,}
(
3
)
{\displaystyle \left({\begin{matrix}3\end{matrix}}\right)\,}
(
1
3
)
{\displaystyle \left({\begin{matrix}1&3\end{matrix}}\right)\,}
(
2
)
{\displaystyle \left({\begin{matrix}2\end{matrix}}\right)\,}
3
{\displaystyle 3\,}
(
1
)
{\displaystyle \left({\begin{matrix}1\end{matrix}}\right)\,}
(
2
)
{\displaystyle \left({\begin{matrix}2\end{matrix}}\right)\,}
(
3
)
{\displaystyle \left({\begin{matrix}3\end{matrix}}\right)\,}
[
3
0
]
=
0
{\displaystyle \left[{\begin{matrix}3\\0\end{matrix}}\right]=0\,}
[
3
1
]
=
2
{\displaystyle \left[{\begin{matrix}3\\1\end{matrix}}\right]=2\,}
[
3
2
]
=
3
{\displaystyle \left[{\begin{matrix}3\\2\end{matrix}}\right]=3\,}
[
3
3
]
=
1
{\displaystyle \left[{\begin{matrix}3\\3\end{matrix}}\right]=1\,}
s
(
n
,
k
)
{\displaystyle s(n,k)\,}
n
=
3
{\displaystyle n=3\,}
与有符号斯特林数类似,无符号斯特林数可以定义为对应递进阶乘 展开式的各项系数,即
(
x
)
n
¯
=
∑
k
=
0
n
[
n
k
]
x
k
{\displaystyle (x)^{\overline {n}}=\sum _{k=0}^{n}\left[{\begin{matrix}n\\k\end{matrix}}\right]x^{k}\,}
其中,
[
n
k
]
{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
0
≤
k
≤
n
{\displaystyle 0\leq k\leq n\,}
[
n
k
]
{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
高斯二项式系数 。
有符号斯特林数和无符号斯特林数有如下关系:
s
(
n
,
k
)
=
(
−
1
)
n
−
k
[
n
k
]
{\displaystyle s(n,k)=(-1)^{n-k}\left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
无符号斯特林数有更多的应用。例如,将
n
{\displaystyle n\,}
k
{\displaystyle k\,}
[
n
k
]
{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
[
4
2
]
=
11
{\displaystyle \left[{\begin{matrix}4\\2\end{matrix}}\right]=11\,}
(A,B)(C,D)
(A,C)(B,D)
(A,D)(B,C)
(A)(B,C,D)
(A)(B,D,C)
(B)(A,C,D)
(B)(A,D,C)
(C)(A,B,D)
(C)(A,D,B)
(D)(A,B,C)
(D)(A,C,B) 或用有向图 [来源请求]
s(4,2)=11 无符号斯特林数有如下递推关系式 :
[
n
+
1
k
]
=
n
[
n
k
]
+
[
n
k
−
1
]
{\displaystyle \left[{\begin{matrix}n+1\\k\end{matrix}}\right]=n\left[{\begin{matrix}n\\k\end{matrix}}\right]+\left[{\begin{matrix}n\\k-1\end{matrix}}\right]\,}
其中,
k
>
0
{\displaystyle k>0}
[
0
0
]
=
1
{\displaystyle \left[{\begin{matrix}0\\0\end{matrix}}\right]=1\,}
[
n
0
]
=
[
0
n
]
=
0
{\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=\left[{\begin{matrix}0\\n\end{matrix}}\right]=0\,}
n
>
0
{\displaystyle n>0}
有符号斯特林数有如下递推关系式:
s
(
n
+
1
,
k
)
=
−
n
s
(
n
,
k
)
+
s
(
n
,
k
−
1
)
{\displaystyle s(n+1,k)=-ns(n,k)+s(n,k-1)}
下表其实是一部分无符号斯特林数,要想获得有符号斯特林数,可以通过它们之间的关系式:
s
(
n
,
k
)
=
(
−
1
)
n
−
k
[
n
k
]
{\displaystyle s(n,k)=(-1)^{n-k}\left[{\begin{matrix}n\\k\end{matrix}}\right]\,}
求得。
k
n
0
1
2
3
4
5
6
0
1
1
0
1
2
0
1
1
3
0
2
3
1
4
0
6
11
6
1
5
0
24
50
35
10
1
6
0
120
274
225
85
15
1
观察前面的“第一类斯特林数表”,我们可以得到一些简单的性质:
[
0
0
]
=
1
{\displaystyle \left[{\begin{matrix}0\\0\end{matrix}}\right]=1\,}
[
n
0
]
=
0
{\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=0\,}
n
>
0
{\displaystyle n>0\,}
如果
k
>
0
{\displaystyle k>0\,}
[
0
k
]
=
0
{\displaystyle \left[{\begin{matrix}0\\k\end{matrix}}\right]=0\,}
或更一般地,如果
k
>
n
{\displaystyle k>n\,}
[
n
k
]
=
0
{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]=0\,}
还有
[
n
1
]
=
(
n
−
1
)
!
{\displaystyle \left[{\begin{matrix}n\\1\end{matrix}}\right]=(n-1)!\,}
[
n
n
]
=
1
{\displaystyle \left[{\begin{matrix}n\\n\end{matrix}}\right]=1\,}
[
n
n
−
1
]
=
(
n
2
)
{\displaystyle \left[{\begin{matrix}n\\n-1\end{matrix}}\right]={n \choose 2}\,}
[
n
n
−
2
]
=
1
4
(
3
n
−
1
)
(
n
3
)
{\displaystyle \left[{\begin{matrix}n\\n-2\end{matrix}}\right]={\frac {1}{4}}(3n-1){n \choose 3}\,}
[
n
n
−
3
]
=
(
n
2
)
(
n
4
)
{\displaystyle \left[{\begin{matrix}n\\n-3\end{matrix}}\right]={n \choose 2}{n \choose 4}\,}
注:这里记号
(
n
k
)
{\displaystyle {n \choose k}\,}
组合数 。
第二类斯特林数 递降阶乘 定义为
x
n
=
∑
k
=
0
n
{
n
k
}
(
x
)
k
{\displaystyle x^{n}=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}(x)_{k}\,}
其中,
{
n
k
}
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,}
[ 2] [ 3]
S
(
n
,
k
)
{\displaystyle S(n,k)\,}
[ 4]
x
3
=
{
3
0
}
(
x
)
0
+
{
3
1
}
(
x
)
1
+
{
3
2
}
(
x
)
2
+
{
3
3
}
(
x
)
3
{\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}(x)_{0}+\left\{{\begin{matrix}3\\1\end{matrix}}\right\}(x)_{1}+\left\{{\begin{matrix}3\\2\end{matrix}}\right\}(x)_{2}+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}(x)_{3}\,}
即
x
3
=
{
3
0
}
+
{
3
1
}
x
+
{
3
2
}
x
(
x
−
1
)
+
{
3
3
}
x
(
x
−
1
)
(
x
−
2
)
{\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}+\left\{{\begin{matrix}3\\1\end{matrix}}\right\}x+\left\{{\begin{matrix}3\\2\end{matrix}}\right\}x(x-1)+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}x(x-1)(x-2)\,}
将递降阶乘展开并合并同类项,得
x
3
=
{
3
0
}
+
(
{
3
1
}
−
{
3
2
}
+
2
{
3
3
}
)
x
+
(
{
3
2
}
−
3
{
3
3
}
)
x
2
+
{
3
3
}
x
3
{\displaystyle x^{3}=\left\{{\begin{matrix}3\\0\end{matrix}}\right\}+\left(\left\{{\begin{matrix}3\\1\end{matrix}}\right\}-\left\{{\begin{matrix}3\\2\end{matrix}}\right\}+2\left\{{\begin{matrix}3\\3\end{matrix}}\right\}\right)x+\left(\left\{{\begin{matrix}3\\2\end{matrix}}\right\}-3\left\{{\begin{matrix}3\\3\end{matrix}}\right\}\right)x^{2}+\left\{{\begin{matrix}3\\3\end{matrix}}\right\}x^{3}\,}
比较等式两边系数,得
{
{
3
0
}
=
0
{
3
1
}
−
{
3
2
}
+
2
{
3
3
}
=
0
{
3
2
}
−
3
{
3
3
}
=
0
{
3
3
}
=
1
{\displaystyle {\begin{cases}\left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\1\end{matrix}}\right\}-\left\{{\begin{matrix}3\\2\end{matrix}}\right\}+2\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\2\end{matrix}}\right\}-3\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=0\\\left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\end{cases}}\,}
解得
{
3
0
}
=
0
{\displaystyle \left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\,}
{
3
1
}
=
1
{\displaystyle \left\{{\begin{matrix}3\\1\end{matrix}}\right\}=1\,}
{
3
2
}
=
3
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\,}
{
3
3
}
=
1
{\displaystyle \left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\,}
第二类斯特林数计算的是将含有
n
{\displaystyle n\,}
k
{\displaystyle k\,}
[ 5]
{
1
,
2
,
3
}
{\displaystyle \left\{1,2,3\right\}\,}
0
{\displaystyle 0\,}
1
{\displaystyle 1\,}
{
1
,
2
,
3
}
{\displaystyle \left\{1,2,3\right\}\,}
2
{\displaystyle 2\,}
{
1
}
{\displaystyle \left\{1\right\}\,}
{
2
,
3
}
{\displaystyle \left\{2,3\right\}\,}
{
1
,
2
}
{\displaystyle \left\{1,2\right\}\,}
{
3
}
{\displaystyle \left\{3\right\}\,}
{
2
}
{\displaystyle \left\{2\right\}\,}
{
1
,
3
}
{\displaystyle \left\{1,3\right\}\,}
3
{\displaystyle 3\,}
{
1
}
{\displaystyle \left\{1\right\}\,}
{
2
}
{\displaystyle \left\{2\right\}\,}
{
3
}
{\displaystyle \left\{3\right\}\,}
{
3
0
}
=
0
{\displaystyle \left\{{\begin{matrix}3\\0\end{matrix}}\right\}=0\,}
{
3
1
}
=
1
{\displaystyle \left\{{\begin{matrix}3\\1\end{matrix}}\right\}=1\,}
{
3
2
}
=
3
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\,}
{
3
3
}
=
1
{\displaystyle \left\{{\begin{matrix}3\\3\end{matrix}}\right\}=1\,}
第二类斯特林数可以使用以下公式进行计算:[ 6]
{
n
k
}
=
1
k
!
∑
i
=
0
k
(
−
1
)
i
(
k
i
)
(
k
−
i
)
n
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}={\frac {1}{k!}}\sum _{i=0}^{k}(-1)^{i}\left({\begin{matrix}k\\i\end{matrix}}\right)(k-i)^{n}\,}
取
{
3
2
}
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}\,}
{
3
2
}
=
1
2
!
∑
i
=
0
2
(
−
1
)
i
(
2
i
)
(
2
−
i
)
3
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2!}}\sum _{i=0}^{2}(-1)^{i}\left({\begin{matrix}2\\i\end{matrix}}\right)(2-i)^{3}\,}
即
{
3
2
}
=
1
2
(
(
2
0
)
×
2
3
−
(
2
1
)
×
1
3
+
(
2
2
)
×
0
3
)
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2}}\left(\left({\begin{matrix}2\\0\end{matrix}}\right)\times 2^{3}-\left({\begin{matrix}2\\1\end{matrix}}\right)\times 1^{3}+\left({\begin{matrix}2\\2\end{matrix}}\right)\times 0^{3}\right)\,}
于是
{
3
2
}
=
1
2
(
1
×
8
−
2
×
1
+
1
×
0
)
=
3
{\displaystyle \left\{{\begin{matrix}3\\2\end{matrix}}\right\}={\frac {1}{2}}\left(1\times 8-2\times 1+1\times 0\right)=3\,}
将
n
{\displaystyle n\,}
k
{\displaystyle k\,}
1
{\displaystyle 1\,}
{
4
1
}
=
1
{\displaystyle \left\{{\begin{matrix}4\\1\end{matrix}}\right\}=1\,}
4
{\displaystyle 4\,}
{
4
4
}
=
1
{\displaystyle \left\{{\begin{matrix}4\\4\end{matrix}}\right\}=1\,}
2
{\displaystyle 2\,}
{甲, 乙}{丙, 丁}
{甲, 丙}{乙,丁}
{甲, 丁}{乙, 丙}
{甲}{乙, 丙, 丁}
{乙}{甲, 丙, 丁}
{丙}{甲, 乙, 丁}
{丁}{甲, 乙, 丙} 因此
{
4
2
}
=
7
{\displaystyle \left\{{\begin{matrix}4\\2\end{matrix}}\right\}=7\,}
{
4
3
}
=
6
{\displaystyle \left\{{\begin{matrix}4\\3\end{matrix}}\right\}=6\,}
第二类斯特林数有与第一类斯特林数类似的递推关系式:
{
n
+
1
k
}
=
k
{
n
k
}
+
{
n
k
−
1
}
{\displaystyle \left\{{\begin{matrix}n+1\\k\end{matrix}}\right\}=k\left\{{\begin{matrix}n\\k\end{matrix}}\right\}+\left\{{\begin{matrix}n\\k-1\end{matrix}}\right\}\,}
其中,
k
>
0
{\displaystyle k>0}
{
0
0
}
=
1
{\displaystyle \left\{{\begin{matrix}0\\0\end{matrix}}\right\}=1\,}
{
n
0
}
=
{
0
n
}
=
0
{\displaystyle \left\{{\begin{matrix}n\\0\end{matrix}}\right\}=\left\{{\begin{matrix}0\\n\end{matrix}}\right\}=0\,}
n
>
0
{\displaystyle n>0}
下面为部分第二类斯特林数:
k
n
0
1
2
3
4
5
6
0
1
1
0
1
2
0
1
1
3
0
1
3
1
4
0
1
7
6
1
5
0
1
15
25
10
1
6
0
1
31
90
65
15
1
观察前面的“第二类斯特林数表”,我们可以得到一些简单的性质:
{
0
0
}
=
1
{\displaystyle \left\{{\begin{matrix}0\\0\end{matrix}}\right\}=1\,}
{
n
0
}
=
0
{\displaystyle \left\{{\begin{matrix}n\\0\end{matrix}}\right\}=0\,}
n
>
0
{\displaystyle n>0\,}
如果
k
>
0
{\displaystyle k>0\,}
{
0
k
}
=
0
{\displaystyle \left\{{\begin{matrix}0\\k\end{matrix}}\right\}=0\,}
或更一般地,如果
k
>
n
{\displaystyle k>n\,}
{
n
k
}
=
0
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}=0\,}
还有
{
n
1
}
=
1
{\displaystyle \left\{{\begin{matrix}n\\1\end{matrix}}\right\}=1\,}
{
n
2
}
=
2
n
−
1
−
1
{\displaystyle \left\{{\begin{matrix}n\\2\end{matrix}}\right\}=2^{n-1}-1\,}
{
n
3
}
=
1
2
(
3
n
−
1
+
1
)
−
2
n
−
1
{\displaystyle \left\{{\begin{matrix}n\\3\end{matrix}}\right\}={\frac {1}{2}}(3^{n-1}+1)-2^{n-1}\,}
{
n
n
}
=
1
{\displaystyle \left\{{\begin{matrix}n\\n\end{matrix}}\right\}=1\,}
{
n
n
−
1
}
=
(
n
2
)
{\displaystyle \left\{{\begin{matrix}n\\n-1\end{matrix}}\right\}={n \choose 2}\,}
{
n
n
−
2
}
=
(
n
3
)
+
3
(
n
4
)
{\displaystyle \left\{{\begin{matrix}n\\n-2\end{matrix}}\right\}={n \choose 3}+3{n \choose 4}\,}
{
n
n
−
3
}
=
(
n
4
)
+
10
(
n
5
)
+
15
(
n
6
)
{\displaystyle \left\{{\begin{matrix}n\\n-3\end{matrix}}\right\}={n \choose 4}+10{n \choose 5}+15{n \choose 6}\,}
贝尔数 和第二类斯特林数有如下关系:
B
n
=
∑
k
=
0
n
{
n
k
}
{\displaystyle B_{n}=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,}
第一类和第二类斯特林数可以看作互为逆矩阵 的关系:
∑
j
≥
0
s
(
n
,
j
)
S
(
j
,
k
)
=
∑
j
≥
0
(
−
1
)
n
−
j
[
n
j
]
{
j
k
}
=
δ
n
k
∑
j
≥
0
s
(
n
,
j
)
S
(
j
,
k
)
=
∑
j
≥
0
(
−
1
)
n
−
j
[
n
j
]
{
j
k
}
=
δ
n
k
{\displaystyle \sum _{j\geq 0}s(n,j)S(j,k)=\sum _{j\geq 0}(-1)^{n-j}{\begin{bmatrix}n\\j\end{bmatrix}}{\begin{Bmatrix}j\\k\end{Bmatrix}}=\delta _{nk}}{\displaystyle \sum _{j\geq 0}s(n,j)S(j,k)=\sum _{j\geq 0}(-1)^{n-j}{\begin{bmatrix}n\\j\end{bmatrix}}{\begin{Bmatrix}j\\k\end{Bmatrix}}=\delta _{nk}\,}
以及
∑
j
≥
0
S
(
n
,
j
)
s
(
j
,
k
)
=
∑
j
≥
0
(
−
1
)
j
−
k
{
n
j
}
[
j
k
]
=
δ
n
k
∑
j
≥
0
S
(
n
,
j
)
s
(
j
,
k
)
=
∑
j
≥
0
(
−
1
)
j
−
k
{
n
j
}
[
j
k
]
=
δ
n
k
{\displaystyle \sum _{j\geq 0}S(n,j)s(j,k)=\sum _{j\geq 0}(-1)^{j-k}{\begin{Bmatrix}n\\j\end{Bmatrix}}{\begin{bmatrix}j\\k\end{bmatrix}}=\delta _{nk}}{\displaystyle \sum _{j\geq 0}S(n,j)s(j,k)=\sum _{j\geq 0}(-1)^{j-k}{\begin{Bmatrix}n\\j\end{Bmatrix}}{\begin{bmatrix}j\\k\end{bmatrix}}=\delta _{nk}\,}
其中,
δ
n
k
{\displaystyle \delta _{nk}\,}
克罗内克尔δ 。
拉赫数 伊沃·拉赫 [ 7] [ 8] 第三类斯特林数 。可以用递进阶乘和递降阶乘 定义为
x
(
n
)
=
∑
k
=
0
n
L
(
n
,
k
)
(
x
)
k
{\displaystyle x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}\,}
或
(
x
)
n
=
∑
k
=
0
n
(
−
1
)
n
−
k
L
(
n
,
k
)
x
(
k
)
{\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}\,}
其中,
L
(
n
,
k
)
{\displaystyle L(n,k)\,}
x
(
3
)
=
∑
k
=
0
3
L
(
3
,
k
)
(
x
)
k
{\displaystyle x^{(3)}=\sum _{k=0}^{3}L(3,k)(x)_{k}\,}
即
x
(
x
+
1
)
(
x
+
2
)
=
L
(
3
,
0
)
⋅
1
+
L
(
3
,
1
)
⋅
x
+
L
(
3
,
2
)
⋅
x
(
x
−
1
)
+
L
(
3
,
3
)
⋅
x
(
x
−
1
)
(
x
−
2
)
{\displaystyle x(x+1)(x+2)=L(3,0)\cdot 1+L(3,1)\cdot x+L(3,2)\cdot x(x-1)+L(3,3)\cdot x(x-1)(x-2)\,}
等式两边展开并合并同类项,得
0
⋅
x
0
+
2
⋅
x
+
3
⋅
x
2
+
1
⋅
x
3
=
L
(
3
,
0
)
+
[
L
(
3
,
1
)
−
L
(
3
,
2
)
+
2
L
(
3
,
3
)
]
⋅
x
+
[
L
(
3
,
2
)
−
3
L
(
3
,
3
)
]
⋅
x
2
+
L
(
3
,
3
)
⋅
x
3
{\displaystyle 0\cdot x^{0}+2\cdot x+3\cdot x^{2}+1\cdot x^{3}=L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[L(3,2)-3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}
比较等式两边系数,得
{
L
(
3
,
0
)
=
0
L
(
3
,
1
)
−
L
(
3
,
2
)
+
2
L
(
3
,
3
)
=
2
L
(
3
,
2
)
−
3
L
(
3
,
3
)
=
3
L
(
3
,
3
)
=
1
{\displaystyle {\begin{cases}{L(3,0)=0}\\{L(3,1)-L(3,2)+2L(3,3)=2}\\{L(3,2)-3L(3,3)=3}\\{L(3,3)=1}\end{cases}}\,}
解得
L
(
3
,
0
)
=
0
{\displaystyle L(3,0)=0\,}
L
(
3
,
1
)
=
6
{\displaystyle L(3,1)=6\,}
L
(
3
,
2
)
=
6
{\displaystyle L(3,2)=6\,}
L
(
3
,
3
)
=
1
{\displaystyle L(3,3)=1\,}
或
(
x
)
3
=
∑
k
=
0
3
(
−
1
)
3
−
k
L
(
3
,
k
)
x
(
3
)
{\displaystyle (x)_{3}=\sum _{k=0}^{3}(-1)^{3-k}L(3,k)x^{(3)}\,}
即
x
(
x
−
1
)
(
x
−
2
)
=
L
(
3
,
0
)
⋅
1
+
L
(
3
,
1
)
⋅
x
+
L
(
3
,
2
)
⋅
x
(
x
+
1
)
+
L
(
3
,
3
)
⋅
x
(
x
+
1
)
(
x
+
2
)
{\displaystyle x(x-1)(x-2)=L(3,0)\cdot 1+L(3,1)\cdot x+L(3,2)\cdot x(x+1)+L(3,3)\cdot x(x+1)(x+2)\,}
等式两边展开并合并同类项,得
0
⋅
x
0
+
2
⋅
x
−
3
⋅
x
2
+
1
⋅
x
3
=
−
L
(
3
,
0
)
+
[
L
(
3
,
1
)
−
L
(
3
,
2
)
+
2
L
(
3
,
3
)
]
⋅
x
+
[
−
L
(
3
,
2
)
+
3
L
(
3
,
3
)
]
⋅
x
2
+
L
(
3
,
3
)
⋅
x
3
{\displaystyle 0\cdot x^{0}+2\cdot x-3\cdot x^{2}+1\cdot x^{3}=-L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[-L(3,2)+3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}
比较等式两边系数,得
{
L
(
3
,
0
)
=
0
L
(
3
,
1
)
−
L
(
3
,
2
)
+
2
L
(
3
,
3
)
=
2
−
L
(
3
,
2
)
+
3
L
(
3
,
3
)
=
−
3
L
(
3
,
3
)
=
1
{\displaystyle {\begin{cases}{L(3,0)=0}\\{L(3,1)-L(3,2)+2L(3,3)=2}\\{-L(3,2)+3L(3,3)=-3}\\{L(3,3)=1}\end{cases}}\,}
解得
L
(
3
,
0
)
=
0
{\displaystyle L(3,0)=0\,}
L
(
3
,
1
)
=
6
{\displaystyle L(3,1)=6\,}
L
(
3
,
2
)
=
6
{\displaystyle L(3,2)=6\,}
L
(
3
,
3
)
=
1
{\displaystyle L(3,3)=1\,}
以上定义的拉赫数是无符号拉赫数(英语: signed Lah numbers),有符号拉赫数(英语:signed Lah numbers)的定义如下:
x
(
n
)
=
(
−
1
)
n
∑
k
=
0
n
L
(
n
,
k
)
(
x
)
k
{\displaystyle x^{(n)}=(-1)^{n}\sum _{k=0}^{n}L(n,k)(x)_{k}\,}
或
(
x
)
n
=
∑
k
=
0
n
(
−
1
)
k
L
(
n
,
k
)
x
(
k
)
{\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{k}L(n,k)x^{(k)}\,}
无符号拉赫数计算的是将含有
n
{\displaystyle n\,}
k
{\displaystyle k\,}
[ 9]
{
1
,
2
,
3
}
{\displaystyle \left\{1,2,3\right\}\,}
0
{\displaystyle 0\,}
1
{\displaystyle 1\,}
{
(
1
,
2
,
3
)
}
{\displaystyle \left\{(1,2,3)\right\}\,}
{
(
1
,
3
,
2
)
}
{\displaystyle \left\{(1,3,2)\right\}\,}
{
(
2
,
1
,
3
)
}
{\displaystyle \left\{(2,1,3)\right\}\,}
{
(
2
,
3
,
1
)
}
{\displaystyle \left\{(2,3,1)\right\}\,}
{
(
3
,
1
,
2
)
}
{\displaystyle \left\{(3,1,2)\right\}\,}
{
(
3
,
2
,
1
)
}
{\displaystyle \left\{(3,2,1)\right\}\,}
2
{\displaystyle 2\,}
{
(
1
)
}
{\displaystyle \left\{(1)\right\}\,}
{
(
2
,
3
)
}
{\displaystyle \left\{(2,3)\right\}\,}
{
(
1
)
}
{\displaystyle \left\{(1)\right\}\,}
{
(
3
,
2
)
}
{\displaystyle \left\{(3,2)\right\}\,}
{
(
2
)
}
{\displaystyle \left\{(2)\right\}\,}
{
(
1
,
3
)
}
{\displaystyle \left\{(1,3)\right\}\,}
{
(
2
)
}
{\displaystyle \left\{(2)\right\}\,}
{
(
3
,
1
)
}
{\displaystyle \left\{(3,1)\right\}\,}
{
(
3
)
}
{\displaystyle \left\{(3)\right\}\,}
{
(
1
,
2
)
}
{\displaystyle \left\{(1,2)\right\}\,}
{
(
3
)
}
{\displaystyle \left\{(3)\right\}\,}
{
(
2
,
1
)
}
{\displaystyle \left\{(2,1)\right\}\,}
3
{\displaystyle 3\,}
{
(
1
)
}
{\displaystyle \left\{(1)\right\}\,}
{
(
2
)
}
{\displaystyle \left\{(2)\right\}\,}
{
(
3
)
}
{\displaystyle \left\{(3)\right\}\,}
L
(
3
,
0
)
=
0
{\displaystyle L(3,0)=0\,}
L
(
3
,
1
)
=
6
{\displaystyle L(3,1)=6\,}
L
(
3
,
2
)
=
6
{\displaystyle L(3,2)=6\,}
L
(
3
,
3
)
=
1
{\displaystyle L(3,3)=1\,}
无符号拉赫数可以使用以下公式进行计算:
L
(
n
,
k
)
=
(
n
−
1
k
−
1
)
n
!
k
!
{\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}\,}
有符号拉赫数可以使用以下公式进行计算:
L
′
(
n
,
k
)
=
(
−
1
)
n
(
n
−
1
k
−
1
)
n
!
k
!
{\displaystyle L'(n,k)=(-1)^{n}{n-1 \choose k-1}{\frac {n!}{k!}}\,}
无符号拉赫数(n 和k 取1到4) 无符号拉赫数有如下递推关系:
L
(
n
,
k
+
1
)
=
n
−
k
k
(
k
+
1
)
L
(
n
,
k
)
{\displaystyle L(n,k+1)={\frac {n-k}{k(k+1)}}L(n,k)}
或
L
(
n
+
1
,
k
)
=
(
n
+
k
)
L
(
n
,
k
)
+
L
(
n
,
k
−
1
)
{\displaystyle L(n+1,k)=(n+k)L(n,k)+L(n,k-1)\,}
其中,
L
(
n
,
0
)
=
0
{\displaystyle L(n,0)=0\,}
L
(
n
,
0
)
=
0
{\displaystyle L(n,0)=0\,}
L
(
n
,
k
)
=
0
{\displaystyle L(n,k)=0\,}
k
>
n
{\displaystyle k>n\,}
L
(
1
,
1
)
=
1
{\displaystyle L(1,1)=1\,}
下面为部分无符号拉赫数:
k
n
0
1
2
3
4
5
6
0
1
1
0
1
2
0
2
1
3
0
6
6
1
4
0
24
36
12
1
5
0
120
240
120
20
1
6
0
720
1800
1200
300
30
1
观察前面的“拉赫数表”,我们可以得到一些简单性质:
L
(
0
,
0
)
=
1
{\displaystyle L(0,0)=1}
L
(
n
,
0
)
=
0
{\displaystyle L(n,0)=0}
n
>
0
{\displaystyle n>0}
如果
k
>
n
{\displaystyle k>n}
L
(
0
,
0
)
=
1
{\displaystyle L(0,0)=1}
L
(
n
,
k
)
=
0
{\displaystyle L(n,k)=0}
还有
L
(
n
,
1
)
=
n
!
{\displaystyle L(n,1)=n!}
L
(
n
,
2
)
=
(
n
−
1
)
n
!
2
{\displaystyle L(n,2)={\frac {(n-1)n!}{2}}}
L
(
n
,
3
)
=
(
n
−
2
)
(
n
−
1
)
n
!
12
{\displaystyle L(n,3)={\frac {(n-2)(n-1)n!}{12}}}
L
(
n
,
n
−
1
)
=
n
(
n
−
1
)
{\displaystyle L(n,n-1)=n(n-1)}
L
(
n
,
n
)
=
1
{\displaystyle L(n,n)=1}
∑
n
≥
k
L
(
n
,
k
)
x
n
n
!
=
1
k
!
(
x
1
−
x
)
k
{\displaystyle \sum _{n\geq k}L(n,k){\frac {x^{n}}{n!}}={\frac {1}{k!}}\left({\frac {x}{1-x}}\right)^{k}}
无符号拉赫数计算公式可以作进一步拓展:
L
(
n
,
k
)
=
(
n
−
1
k
−
1
)
n
!
k
!
=
(
n
k
)
(
n
−
1
)
!
(
k
−
1
)
!
=
(
n
k
)
(
n
−
1
k
−
1
)
(
n
−
k
)
!
{\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}={n \choose k}{\frac {(n-1)!}{(k-1)!}}={n \choose k}{n-1 \choose k-1}(n-k)!}
L
(
n
,
k
)
=
n
!
(
n
−
1
)
!
k
!
(
k
−
1
)
!
⋅
1
(
n
−
k
)
!
=
(
n
!
k
!
)
2
k
n
(
n
−
k
)
!
{\displaystyle L(n,k)={\frac {n!(n-1)!}{k!(k-1)!}}\cdot {\frac {1}{(n-k)!}}=\left({\frac {n!}{k!}}\right)^{2}{\frac {k}{n(n-k)!}}}
无符号拉赫数与两类斯特林数都有关系[ 10]
L
(
n
,
k
)
=
∑
j
=
0
n
[
n
j
]
{
j
k
}
{\displaystyle L(n,k)=\sum _{j=0}^{n}\left[{\begin{matrix}n\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\k\end{matrix}}\right\}\,}
取
L
(
3
,
2
)
{\displaystyle L(3,2)\,}
L
(
3
,
2
)
=
∑
j
=
0
3
[
3
j
]
{
j
2
}
{\displaystyle L(3,2)=\sum _{j=0}^{3}\left[{\begin{matrix}3\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\2\end{matrix}}\right\}\,}
即
L
(
3
,
2
)
=
[
3
0
]
{
0
2
}
+
[
3
1
]
{
1
2
}
+
[
3
2
]
{
2
2
}
+
[
3
3
]
{
3
2
}
{\displaystyle L(3,2)=\left[{\begin{matrix}3\\0\end{matrix}}\right]\left\{{\begin{matrix}0\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\1\end{matrix}}\right]\left\{{\begin{matrix}1\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}\,}
于是
L
(
3
,
2
)
=
[
3
2
]
{
2
2
}
+
[
3
3
]
{
3
2
}
=
3
×
1
+
1
×
3
=
6
{\displaystyle L(3,2)=\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\times 1+1\times 3=6\,}
由无符号拉赫数与两类斯特林数之间的关系,考虑到两类斯特林数之间的关系,有
∑
j
≥
0
L
(
n
,
j
)
L
(
j
,
k
)
=
δ
n
k
{\displaystyle \sum _{j\geq 0}L(n,j)L(j,k)=\delta _{nk}\,}
其中,
δ
n
k
{\displaystyle \delta _{nk}\,}
克罗内克尔δ 。
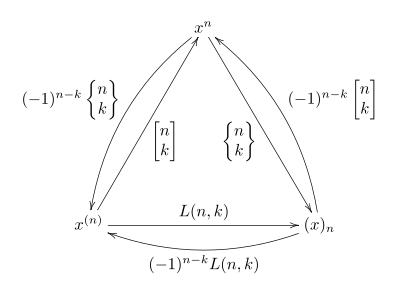
三类斯特林数以及乘方、阶乘之间的关系可以用下图表示:
^ Sándor, Jozsef; Crstici, Borislav. Handbook of Number Theory II. Kluwer Academic Publishers. 2004: 464. ISBN 9781402025464 ^ Transformation of Series by a Variant of Stirling's Numbers. Imanuel Marx, The American Mathematical Monthly 69, #6 (June–July 1962). : 530–532,. JSTOR 2311194. ^ Antonio Salmeri (编). Introduzione alla teoria dei coefficienti fattoriali, Giornale di Matematiche di Battaglini 90 (1962). : pp. 44–54. ^ Knuth, D.E. (1992) (编). "Two notes on notation", Amer. Math. Monthly, 99. : 403-422. JSTOR 2325085 arXiv:math/9205211 doi:10.2307/2325085 ^ Brualdi,R.A. (编). 组合数学(原书第5版). 由冯速等人翻译. 北京: 机械工业出版社. 2012.4: 176页. ISBN 978-7-111-37787-0 ^ Weisstein, Eric W. (编). " Stirling Number of the Second Kind" MathWorld Wolfram Research, Inc. [2019-06-06 ] . (原始内容存档 于2019-06-06) (英语) . ^ Lah, Ivo. A new kind of numbers and its application in the actuarial mathematics 9 . 1954: 7–15. ^ John Riordan, Introduction to Combinatorial Analysis (页面存档备份 ,存于互联网档案馆 ), Princeton University Press (1958, reissue 1980) ISBN 978-0-691-02365-6 (reprinted again in 2002 by Dover Publications).^ Petkovsek, Marko; Pisanski, Tomaz. Combinatorial Interpretation of Unsigned Stirling and Lah Numbers 12 . Fall 2007: 417–424. JSTOR 24340704 ^ Comtet, Louis. Advanced Combinatorics . Dordrecht, Holland: Reidel. 1974: 156 .


 . doi:10.2307/2325085.
. doi:10.2307/2325085.














![{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9e2dcd620ff6f0a2f0b3651658da929e65cfc71)












![{\displaystyle \left[{\begin{matrix}3\\0\end{matrix}}\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6608dc355dddd96e42446d0e6a6631074afe588)
![{\displaystyle \left[{\begin{matrix}3\\1\end{matrix}}\right]=2\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f1c4c52881cfe42820fe162a7c27e6379d574b7)
![{\displaystyle \left[{\begin{matrix}3\\2\end{matrix}}\right]=3\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5267ba000b8510c4bcb22473c2a7b5a8e569ccb8)
![{\displaystyle \left[{\begin{matrix}3\\3\end{matrix}}\right]=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48304dc0c643b1984be652efd337cb793a3fba25)

![{\displaystyle (x)^{\overline {n}}=\sum _{k=0}^{n}\left[{\begin{matrix}n\\k\end{matrix}}\right]x^{k}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e3cfb0f3973e236502074d32e407a47765b8f2a)
![{\displaystyle s(n,k)=(-1)^{n-k}\left[{\begin{matrix}n\\k\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c438825a4f99ee75e0044d9d7bd6faea75225b)
![{\displaystyle \left[{\begin{matrix}4\\2\end{matrix}}\right]=11\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7e1bd90170c0e24881bfee15f40c1a2fdae686d)
![{\displaystyle \left[{\begin{matrix}n+1\\k\end{matrix}}\right]=n\left[{\begin{matrix}n\\k\end{matrix}}\right]+\left[{\begin{matrix}n\\k-1\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/933aa21a11d96f9172e2156949f765b32aae68e7)

![{\displaystyle \left[{\begin{matrix}0\\0\end{matrix}}\right]=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/630102b23733ec253ae7d9fb7b03630bdc914a09)
![{\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=\left[{\begin{matrix}0\\n\end{matrix}}\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/687dc337a2789054373d643f4a65d70dc6e134d0)


![{\displaystyle \left[{\begin{matrix}n\\0\end{matrix}}\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc494e6e247b6994c680cfbd3a392f64c67b7f7)


![{\displaystyle \left[{\begin{matrix}0\\k\end{matrix}}\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f55f16b53e1949a4a27b6b066e6dd4883d869ab)

![{\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26f3d1629e4dea2d4910e74646b562ba2e24ef57)
![{\displaystyle \left[{\begin{matrix}n\\1\end{matrix}}\right]=(n-1)!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1e596fa499b0eb90e96162cb166bb5d27f6589e)
![{\displaystyle \left[{\begin{matrix}n\\n\end{matrix}}\right]=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27ad3cb7600db3ba2c5f2a8837bb76c1e080a0d)
![{\displaystyle \left[{\begin{matrix}n\\n-1\end{matrix}}\right]={n \choose 2}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e0ed8f4754ad3cf2f6be65f9596ff025ff95f3f)
![{\displaystyle \left[{\begin{matrix}n\\n-2\end{matrix}}\right]={\frac {1}{4}}(3n-1){n \choose 3}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e57c4c2c4999dc9aa742b1a2d2f0a4e89daf02)
![{\displaystyle \left[{\begin{matrix}n\\n-3\end{matrix}}\right]={n \choose 2}{n \choose 4}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e848b5b6c7befd938ec31f81f63dc477a294f0e6)



















































![{\displaystyle 0\cdot x^{0}+2\cdot x+3\cdot x^{2}+1\cdot x^{3}=L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[L(3,2)-3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7049bb61bb751d55f24ef431dcb488f25afe5a)







![{\displaystyle 0\cdot x^{0}+2\cdot x-3\cdot x^{2}+1\cdot x^{3}=-L(3,0)+[L(3,1)-L(3,2)+2L(3,3)]\cdot x+[-L(3,2)+3L(3,3)]\cdot x^{2}+L(3,3)\cdot x^{3}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e23ff470f03d8b95368e57b270b73f63a23d972)





































![{\displaystyle L(n,k)=\sum _{j=0}^{n}\left[{\begin{matrix}n\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\k\end{matrix}}\right\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027b0652ca6577e9185ed805e61edf768c6942cc)

![{\displaystyle L(3,2)=\sum _{j=0}^{3}\left[{\begin{matrix}3\\j\end{matrix}}\right]\left\{{\begin{matrix}j\\2\end{matrix}}\right\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/974d54a24f56da30646d2d291fb6421b172d7642)
![{\displaystyle L(3,2)=\left[{\begin{matrix}3\\0\end{matrix}}\right]\left\{{\begin{matrix}0\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\1\end{matrix}}\right]\left\{{\begin{matrix}1\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df897990460189efa1ff5267f139f066ca1b6a2b)
![{\displaystyle L(3,2)=\left[{\begin{matrix}3\\2\end{matrix}}\right]\left\{{\begin{matrix}2\\2\end{matrix}}\right\}+\left[{\begin{matrix}3\\3\end{matrix}}\right]\left\{{\begin{matrix}3\\2\end{matrix}}\right\}=3\times 1+1\times 3=6\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7430c52d0c892cd2071d88787b03e8a8c0cebb05)