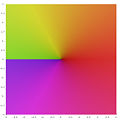
色相环复变函数图形


色相环复变函数图形是一种复变函数图形的呈现方式,是一种饱和度固定为最饱和,将色相表示函数值的辐角、明度表示函数值的绝对值来表达复变函数的定义域着色方法[1],这种方法又称为色相环法(color wheel method)[2]。
历史
[编辑]使用色相环法的定义域着色早在1980年代末就已被拉里·柯荣(英语:Larry Crone)和汉斯·隆达马克(Hans Lundmark)首先使用。但与之相关的其他的复变函数绘图直到1998年左右时由法兰克·菲莉丝(英语:Frank Farris)统整并统称为定义域着色[3]。
方法
[编辑]

这种函数图形表示方有有两种:
- 另一种原点是白色、1为红色、-1是青色、无限大为黑色:
- 另外也有类似第一种的上色方式:原点是黑色、1为红色、-1是青色、无限大为白色:
更确切地说,复数的辐角(角度)以色相来表示,而模量(绝对值)以HLS色彩模型(色调、亮度、饱和度)中的亮度来表示;对于给定的(H, L)数对,在这个模型中选择最大饱和度值来呈现指定的复数。这几种上色方式,最鲜艳的颜色以旋转的方式出现在复数高斯平面的单位圆上,根据面两种定义,1的六个六次方根(从1开始、逆时针)颜色分别为红色、黄色、绿色、青蓝、蓝色和洋红。此外,在这种配置上,两个非常接近的复数其亮度值也会非常接近,若其辐角相同,则绝对值较大者,根据第一和最后一种定义,其颜色会较浅;根据第二种定义,其颜色会较深,反之亦然。
然而,HSL色彩空间在视觉上并不均匀,而导致在黄色、青色和品红色表达的复数出现亮度差异的条纹,即使其绝对值与红色、绿色和蓝色相同条纹仍明显可见,在单位圆上()附近也可以见到一圈明显的晕圈。Lab等色彩空间更加接近人类感知,可以校正HSL的不均匀问题,使图像视觉上更准确、更加柔和[注 1]。
针对色相环复变函数图形,为了使图像具可比较性,数学函数数位图书馆(The Digital Library of Mathematical Functions, DLMF)对此定义了一套标准的色彩配置方式[4]。
复数色彩空间
[编辑]复数色彩空间是这种定义域着色方法的色彩空间,每个复数皆有对应唯一一种颜色,但是由于其定义上饱和度为定值,因此在这个色彩空间中并非所有色彩都能对应到一个复数。但这种色彩空间和HSL色彩空间一样在视觉上有不均匀的缺点,因此数位图书馆有一套将标准色相环进行微调,其将单位为弧度的色相值以映射到q,然后以公式换算[4]:
其他上色方式
[编辑]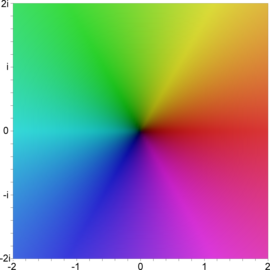
亦有另外一种依据色相上色的定义域着色方法,其依据HSV上色,但是饱和度不取定值,明度与饱和度取决于绝对值的对数值,在表达复数上比前者仅用亮度变化表示复数的方式能得到更多反差,但由于仍属于色相环色彩空间,因此仍有视觉不平均问题。
以绝对值的明度或亮度以对数或指数倒数来表示复变函数图形分别有不同的用途,例如对数成长较慢,因此当值域数字差异很大时适合使用绝对值以对数值来上色的版本,而指数倒数则适用于值域数字相当小的复变函数,例如绝对值在零与一之间震荡的函数。
这种明度与饱和度取决于绝对值的对数值一般会定义为[5]:
其中r为绝对值取对数的结果,a、b、c是调整结果用的系数。
参见
[编辑]注解
[编辑]参考文献
[编辑]- ^ Color Graphs of Complex Functions. 美利坚大学. [2017-03-17]. (原始内容存档于2012-05-11).
- ^ Color wheel method. 塞格德大学数学系. 2005-10-22 [2017-03-17]. (原始内容存档于2007-01-01).
- ^ Frank A. Farris. Visualizing complex-valued functions in the plane. [2017-03-17]. (原始内容存档于2012-12-30).
- ^ 4.0 4.1 存档副本 Digital Library of Mathematical Functions: Continuous Phase Mapping. [2016-01-06]. (原始内容存档于2016-02-28).
- ^ Complex Domain Coloring using fztopng. jedsoft.org. [2017-05-28]. (原始内容存档于2017-01-07).