正十二面体

正十二面体

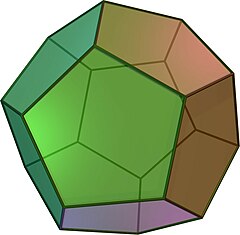(按这里观看旋转模型)
类别	帕雷托立体 正多面体
对偶多面体	正二十面体
识别
名称	正十二面体
参考索引	U23, C26, W5
鲍尔斯缩写	doe
数学表示法
施莱夫利符号	{5,3}
威佐夫符号	3 | 2 5
康威表示法	D
性质
面	12
边	30
顶点	20
欧拉特征数	F=12, E=30, V=20 （χ=2）
二面角	116.56505° = arccos(-1/√5)
组成与布局
面的种类	正五边形
面的布局	12个{5}
顶点图	5.5.5
对称性
对称群	Ih
特性
正凸多面体
图像
5.5.5 （顶点图） （展开图）

正十二面体是由12个正五边形所组成的正多面体，它共有20个顶点、30条棱、160条对角线，被施莱夫利符号{5,3}所表示，与正二十面体互成对偶。它是一种只具有正四面体对称性的五角十二面体的特殊形式，五角十二面体的另一种特殊形式是具有正八面体对称性的卡塔兰多面体菱形十二面体，它（加上所有其它的五角十二面体）都与正十二面体在拓扑上等价。正十二面体还是截顶五方偏方面体的特例。其四维类比为正一百二十胞体。

十二面体

正十二面体是正二十面体的对偶多面体。

性质

面的图形：正五边形
面的数目：12
边的数目：30
顶点数目：20
二面角角度：${\boldsymbol {\theta }}=\arccos \left(-{\frac {1}{\sqrt {5}}}\right)=2\arctan \varphi \approx 116.5650512^{\circ }$
如果正十二面体棱长为a：
表面积：$A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.645728807a^{2}$
体积：$V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.6631189606a^{3}$
外接球半径：$r_{u}=a{\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\approx 1.401258538\cdot a$
内切球半径：$r_{i}=a{\frac {1}{2}}{\sqrt {{\frac {5}{2}}+{\frac {11}{10}}{\sqrt {5}}}}\approx 1.113516364\cdot a$
中分球半径：$r_{m}=a{\frac {1}{4}}\left(3+{\sqrt {5}}\right)\approx 1.309016994\cdot a$

• 我们亦可以将上述三式写作：

外接球半径：$r_{u}=a\,{\frac {\sqrt {3}}{2}}\varphi$

内切球半径：$r_{i}=a\,{\frac {\varphi ^{2}}{2{\sqrt {3-\varphi }}}}$

中分球半径：$r_{m}=a\,{\frac {\varphi ^{2}}{2}}$

（在这里φ是黄金分割数，φ = ^1+√5/₂）

• 注意到棱长为a的正十二面体的外接球同样外接于棱长为φa的立方体，并且其内切球半径（也即面心距）等于棱长为φa的正五边形的边心距。

对偶多面体：正二十面体

坐标系

顶点坐标：
	橙色的顶点位于(±1, ±1, ±1)，形成了其一个内接立方体(虚线所示)。
	绿色的顶点位于(0, ±φ, ±1/φ)，形成了y–z平面上的一个矩形。
	蓝色的顶点位于(±1/φ, 0, ±φ)，形成了x–z平面上的一个矩形。
	粉色的顶点位于(±φ, ±1/φ, 0)，形成了x–y平面上的一个矩形。
相邻顶点间的距离是2/φ，顶点到原点的距离是√3. φ = (1 + √5) / 2是黄金分割数。

如果我们以正十二面体的形心为原点建立三维直角坐标系，那么其20个顶点可被描述为：
(0,±φ,±1/φ)
(±1/φ,0,±φ)
(±φ,±1/φ,0)
(±1,±1,±1)
其中φ = (1+√5)/2，是黄金分割数，也被写作τ，约等于1.618。
该正十二面体棱长为²/_φ=√5–1。其外接球半径正好为√3。

二维投影和对称性

正十二面体有两种特殊的正交投影，分别正对着其一个顶点和一个正五边形面，对应着A₂和H₂考克斯特平面

正交投影

正对于	顶点	棱	面
图像
投影 对称性	[[3]] = [6]	[2]	[[5]] = [10]

在透视投影中，如果如果投影中心正在正十二面体外接球正对其一面的一点，则你能得到其施莱格尔图像，我们亦可以将其视为球面多面体而使用球极投影。这些方法也被用于可视化其四维类比正一百二十胞体，一个由120个全等的正十二面体组成的四维凸正多胞体。

投影	正交投影	透视投影
		施莱格尔图像	球极投影
正十二面体
正120胞体

几何关联

• 正十二面体是一个无穷家族——截对角偏方面体的第3个成员（截对角五方偏方面体）。这类多面体可以被看作是将偏方面体在旋转对称轴上的两个相对的顶点截去而成。
• 正十二面体的星形化体构成了4个星形正多面体中的3个。
• 我们可以在正十二面体的20个顶点中选取5组这样的顶点，使任意两个顶点的连线都是正十二面体正五边形面的一条对角线，这样能构成正十二面体的内接立方体，5个内接立方体一起构成了——复合多面体——五复合立方体；我们还可以进一步对内接立方体做交错操作，得到正十二面体的内接正四面体，如果我们只在内接立方体中取一个正四面体，则5个正四面体构成了有手征性的复合多面体——五复合四面体；如果取两个，则10个正四面体构成了复合多面体——十复合四面体，这三个复合多面体都是正十二面体的小面化体。
• 正十二面体的完全对称群是正二十面体对称群I_h，考克斯特群[5,3]，群阶120，还有一个抽象群结构A₅×Z₂。

与其对偶——正二十面体的关系

• 当正十二面体和正二十面体内接于同一球时，尽管正二十面体有更多的面，但正十二面体占据球的体积（66.49%）要多于正二十面体占据的球的体积（60.54%），这一点与二维不同。
• 棱长相同为1的正十二面体的体积（7.663...）是正二十面体体积（2.181...）的三倍半多。

相关多面体

正十二面体在拓扑上与一系列三阶正镶嵌（顶点图为n³）有关：

多面体				欧式镶嵌	双曲镶嵌
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	...	{∞,3}

正十二面体在拓扑上还和其它阶的正五边形正镶嵌{5,n}(n≥3)有关：

多面体		欧式镶嵌	双曲镶嵌
{5,2}	{5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}	...	{5,∞}

正十二面体可以通过不同类型的截取操作来得到一系列不同的半正多面体及其对偶，正二十面体，构成了正二十面体家族：

正二十面体家族半正多面体

对称群: [5,3], (*532)							[5,3]+, (532)
{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}
半正多面体对偶
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

顶点分布

正十二面体与4个星形半正多面体和上述3个复合半正多面体有同样的顶点分布：

大星形十二面体	小双三斜三十二面体	双三斜二十四面体	大双三斜三十二面体
五复合立方体	五复合四面体	十复合四面体

星形化体

正十二面体的3个星形化体都是星形正多面体（开普勒-普索多面体）：

	0	1	2	3
星形化体	正十二面体	小星形十二面体	大十二面体	大星形十二面体
表面图形

倒角多面体

类别	帕雷托立体					卡塔兰立体
种子	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	aC	aD
倒角	cT	cC	cO	cD	cI	caC	caD

相关数学问题

• 哈密顿路径的理论就是源自一个和正十二面体有关的问题：试求一条路径，沿正十二面体的棱经过它所有的顶点。

应用

• 因为一年有12个月，正十二面体正好用来制作月历。
• Pariacoto virus的形状结构是正十二面体。
• 在英国到匈牙利，至到意大利东部等地，找到过百个形状接近十二面体、以铜或石头制造的空心对象。它们被称为Dodecaeder，用途不明。
• 五魔方（Megaminx）就是正十二面体制作出来的魔方。

正十二面烷

化学：

• 硫化铁结晶体有时会出现接近正十二面体的形状。
• 最小的富勒烯C₂₀结构如正十二面体。
• 正十二面体烷C₂₀H₂₀是个人工合成的碳氢化合物

参考文献

1. 埃里克·韦斯坦因. Dodecahedron. MathWorld. 
2. 埃里克·韦斯坦因. Elongated Dodecahedron. MathWorld. 
3. Klitzing, Richard. 3D convex uniform polyhedra o3o5x – doe. bendwavy.org. 
4. Editable printable net of a dodecahedron with interactive 3D view （页面存档备份，存于互联网档案馆）
5. The Uniform Polyhedra （页面存档备份，存于互联网档案馆）
6. Origami Polyhedra （页面存档备份，存于互联网档案馆） – Models made with Modular Origami
7. Dodecahedron （页面存档备份，存于互联网档案馆） – 3-d model that works in your browser
8. Virtual Reality Polyhedra （页面存档备份，存于互联网档案馆） The Encyclopedia of Polyhedra
   • VRML models
   1. Regular dodecahedron （页面存档备份，存于互联网档案馆） regular
   2. Rhombic dodecahedron （页面存档备份，存于互联网档案馆） quasiregular
   3. Decagonal prism （页面存档备份，存于互联网档案馆） vertex-transitive
   4. Pentagonal antiprism （页面存档备份，存于互联网档案馆） vertex-transitive
   5. Hexagonal dipyramid （页面存档备份，存于互联网档案馆） face-transitive
   6. Triakis tetrahedron （页面存档备份，存于互联网档案馆） face-transitive
   7. hexagonal trapezohedron （页面存档备份，存于互联网档案馆） face-transitive
   8. Pentagonal cupola （页面存档备份，存于互联网档案馆） regular faces
9. K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra （页面存档备份，存于互联网档案馆）
10. Dodecahedron 3D Visualization （页面存档备份，存于互联网档案馆）
11. Stella: Polyhedron Navigator （页面存档备份，存于互联网档案馆）: Software used to create some of the images on this page.

外部链接

• 埃里克·韦斯坦因, 正十二面体 （参阅帕雷托立体） 于MathWorld（英文）