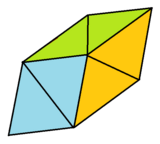
三方偏方面体
外观
 | |
| 类别 | 偏方面体 |
|---|---|
| 对偶多面体 | 三角反棱柱 |
| 数学表示法 | |
| 考克斯特符号 | |
| 性质 | |
| 面 | 6 菱形 |
| 边 | 12 |
| 顶点 | 8 |
| 欧拉特征数 | F=6, E=12, V=8 (χ=2) |
| 组成与布局 | |
| 面的布局 | 3,3,3,3 |
| 对称性 | |
| 对称群 | D3d, [2+,6], (2*3), order 12 |
| 旋转对称群 | D3, [2,6]+, (223), order 6 |
| 特性 | |
| 凸、面可递 | |
在几何学中,三方偏方面体(英语:Trigonal Trapezohedron)又称为又称三方偏四角面体[1]、三角筝形多面体(英语:Trigonal Deltohedron)或双反三角锥(英语:Trigonal Antidipyramid)是一个由六个全等的菱形组成的立体图形,是六面体的一种,亦是平行六面体的特例,因其可视为由六个全等且等边长的平行四边形所组成。因为所有的边缘都必须具有相同的长度,因此每一个三方偏方面体也是筝形多面体。
三方偏方面体是最简单的偏方面体无穷序列(即:三方偏方面体、四方偏方面体、五方、六方、七方......)即最简单的反棱柱对偶多面体的无穷序列(二方偏方面体已退化为四面体)。
若三方偏方面体组成的菱形不只等边且等角,此种三方偏方面体就是一个正六面体,即正方体或立方体,因为其面为正方形,因此若三方偏方面体的面维正方形就会是正多面体,反之,立方体就是三方偏方面体中的一个特例。
相关多面体
[编辑]利用两个四面域扩张八面体而建立的三方偏方面体,可以视为一个由十二个正三角形组成的非严格凸十二面体,然而其三角形两两共面形成60度菱形的面,因此不算约翰逊多面体,但可以算是一种拟约翰逊多面体。
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
|||
| 球面投影 | |||||||||||

|

|

|

|

|

|

|

|

|
|||
三方偏方面体是三角反角柱的对偶多面体,而三角反角柱可以由三角形二面体透过扭棱变换构造而来,因此与三角形二面体具有相同的对称性,其可以衍生出一些相关的多面体:
| 对称群:[3,2], (*322) | [3,2]+, (322) | ||||||||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

| ||||
| {3,2} |
t{3,2} |
r{3,2} |
2t{3,2}=t{2,3} | 2r{3,2}={2,3} | rr{3,2} | tr{3,2} | sr{3,2} | ||
| 半正对偶 | |||||||||

|

|

|

|

|

|

|

| ||
| V32 | V62 | V32 | V4.4.3 | V23 | V4.4.3 | V4.4.6 | V3.3.3.3 | ||
参见
[编辑]参考文献
[编辑]- ^ 苏伟昭. 晶形與其對應平面展開圖演算法與實作 (PDF). 物理教育学刊. 2019-12-01, 20 (2): 49–70 [2023-01-11]. ISSN 1998-7544. doi:10.6212/CPE.201912_20(2).0004.