跳转到内容

六角四片四角孔扭歪无限面体

编辑链接
本页使用了标题或全文手工转换
维基百科，自由的百科全书
六角四片四角孔扭歪无限面体
六角四片四角孔扭歪无限面体
（单击查看旋转模型）
类别正扭歪无限面体
对偶多面体四角六片四角孔扭歪无限面体
识别
鲍尔斯缩写
（verse-and-dimensions的wikia：Bowers acronym）		muo在维基数据编辑
数学表示法
考克斯特符号
（英语：Coxeter-Dynkin diagram）		branch_11 4a4b nodes 
施莱夫利符号{6,4|4}
性质
面无限个正六边形
边无限
顶点无限
4个正六边形的公共顶点
组成与布局
顶点图扭歪四边形
{4}#{ }
顶点布局
（英语：Vertex_configuration）		同于截角八面体堆砌
特性
扭歪、点可递
图像
立体图
扭歪四边形
{4}#{ }
（顶点图）

四角六片四角孔扭歪无限面体
（对偶多面体）

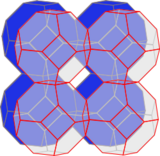
在几何学中，六角四片四角孔扭歪无限面体 （英语：muoctahedron、日语：六角四片四角孔ねじれ正多面体[1]）是一种正扭歪无限面体，是一个由六边形组成且发散的多面体，其多面体所形成的结构无法包覆一个三维空间区域，因此属于扭歪多面体，其可以视为从截角八面体堆砌（截角八面体的空间填充的形状）中移除所有正方形之后所形成的几何结构。

性质

[编辑]

六角四片四角孔扭歪无限面体由无限多个正六边形组成[2]，具有无线条边和无限多个顶点，每个顶点都是4个正六边形的公共顶点，并具有正方形的孔洞，在施莱夫利符号中可以用{6,4|4}来表示，在顶点图中，亦能使用6.6.6.6来表示[3]，其对偶多面体为四角六片四角孔扭歪无限面体[4]。

二面角

[编辑]

六角四片四角孔扭歪无限面体由无限多个正六边形组成，每个正六边形与正六边形的夹角以扭歪的形式交错以截角八面体的六边形-六边形二面角与其反角组成，其角度等于截角八面体的六边形-六边形二面角[5]：

由于其角为正角与反角交错，因而使其所形成的几何结构发散，并形成了具有特定孔洞的几何结构，此种几何结构最早由考克斯特描述[6][7]。

六角四片四角孔扭歪无限面体顶角与二面角的构成模式
六角四片四角孔扭歪无限面体顶角示意图，蓝色为其构成面。

顶角的组成

[编辑]

六角四片四角孔扭歪无限面体每个顶角都是由四个六边形构成的四面角，由于其二面角的交错结构，因此其顶点图是一个扭歪四边形，换句话说即其顶角沿线切开后的形状不是一个凸多边形

用途

[编辑]

六角四片四角孔扭歪无限面体通常用于装置艺术，例如茶几、猫的藏身处、透过其孔洞制造气氛照明装置或做成可堆叠雕塑[2]。

相关多面体

[编辑]

对偶复合体

[编辑]
复合四角六片四角孔扭歪无限面体六角四片四角孔扭歪无限面体
六角四片四角孔扭歪无限面体
复合四角六片四角孔扭歪无限面体六角四片四角孔扭歪无限面体
类别复合正扭歪无限多面体
对偶多面体自身对偶
性质
体2
面无限个正六边形
无限个正方形
边无限
顶点无限
4个正六边形的公共顶点
6个正方形的公共顶点
组成与布局
复合几何体数量2
复合几何体种类1个四角六片四角孔扭歪无限面体
1个六角四片四角孔扭歪无限面体

对偶复合体，即一个多面体与其对偶多面体组合成的复合图形。六角四片四角孔扭歪无限面体为复合四角六片四角孔扭歪无限面体六角四片四角孔扭歪无限面体，在施莱夫利符号中用{4,6|4}{6,4|4}表示。

相关堆砌体

[编辑]
主条目：截角八面体堆砌

六角四片四角孔扭歪无限面体可以看做是由截角八面体的空间填充的形状——截角八面体堆砌中移除所有正方形面、只保留正六边形面的后所形成的扭歪无限面体[8]，因此，六角四片四角孔扭歪无限面体与截角八面体堆砌有着相同的顶点布局。

六角四片四角孔扭歪无限面体
六角四片四角孔扭歪无限面体 		骨架图
截角八面体堆砌与
六角四片四角孔扭歪无限面体
的骨架图相同 		截角八面体堆砌
截角八面体堆砌

正扭歪无限面体

[编辑]

六角四片四角孔扭歪无限面体是三种正扭歪无限面体之一，另外两种为[10]：

图像
四角六片四角孔扭歪无限面体
六角四片四角孔扭歪无限面体
六角六片三角孔扭歪无限面体
施莱夫利符号 {4,6|4} {6,4|4} {6,6|3}

商空间

[编辑]

六角四片四角孔扭歪无限面体在拓朴中相当于四阶六边形镶嵌（施莱夫利符号：{6,4}）的商空间[11]，即六角四片四角孔扭歪无限面体可透过拓朴变形成四阶六边形镶嵌。

其他六角扭歪无限面体

[编辑]

有些扭歪无限面体也是由六边形组成的，例如六角六片三角孔扭歪无限面体。

参见

[编辑]


参考文献

[编辑]
  1. ^ 1.0 1.1 正多面体を解く. Tokai library. 东海大学出版会. 2002 [2018-09-02]. ISBN 9784486015871. （原始内容存档于2018-09-02）. 
  2. ^ 2.0 2.1 Apeirohedron stool. voukenaspetrides.com. [2019-05-04]. （原始内容存档于2020-02-10）. 
  3. ^ Yackel, C. and belcastro, sarah-marie. Figuring Fibers. Miscellaneous Books. American Mathematical Society. 2018 [2019-05-04]. ISBN 9781470429317. （原始内容存档于2019-11-29）. 
  4. ^ kotetu. 準結晶とウイルスの意外な関係. eonet.ne.jp. 2017-03-31 [2018-09-02]. （原始内容存档于2017-08-13）. 
  5. ^ Archimedean Solids: TruncatedOctahedron. dmccooey.com. [2019-05-05]. （原始内容存档于2019-10-31）. 
  6. ^ Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
  7. ^ Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
  8. ^ 正多面体を解く2002 [1] 第6章　ねじれ正多面体：ねじれ多面体の具体的构成法
  9. ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
  10. ^ The Symmetry of Things, 2008[9], Chapter 23 Objects with Primary Symmetry, Infinite Platonic Polyhedra, pp. 333–335
  11. ^ Lee, Dami. Geometric realizations of cyclically branched coverings over punctured spheres (PDF). arXiv preprint arXiv:1809.06321. 2018 [2019-05-05]. （原始内容存档 (PDF)于2019-05-05）. 
检索自“https://zh.wikipedia.org/w/index.php?title=六角四片四角孔扭歪無限面體&oldid=75192129#複合四角六片四角孔扭歪無限面體六角四片四角孔扭歪無限面體”