欧氏平面几何中,婆罗摩笈多公式是用以计算圆内接四边形的面积的公式,以印度数学家婆罗摩笈多之名命名。一般四边形的面积公式请见布雷特施奈德公式。
婆罗摩笈多公式的最简单易记的形式,是圆内接四边形面积计算。若圆内接四边形的四边长为 ,
,  ,
,  ,
,  ,则其面积为:
,则其面积为:

其中 为半周长:
为半周长:

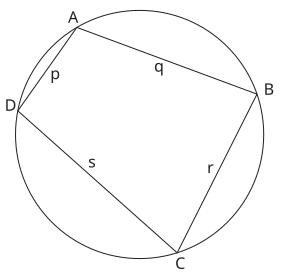
圆内接四边形的面积 =  的面积 +
的面积 +  的面积
的面积

但由于 是圆内接四边形,因此
是圆内接四边形,因此 。故
。故 。所以:
。所以:




对 和
和 利用余弦定理,我们有:
利用余弦定理,我们有:

代入 (这是由于
(这是由于 和
和 是互补角),并整理,得:
是互补角),并整理,得:

把这个等式代入面积的公式中,得:


它是 的形式,因此可以写成
的形式,因此可以写成 的形式:
的形式:

![{\displaystyle =[(p+q)^{2}-(r-s)^{2}][(r+s)^{2}-(p-q)^{2}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/389f3fb3ec2407821704c894329c2981798621ed)

引入 ,
,

两边开平方,得:

证毕。
若圆 的圆内接四边形的四边长为
的圆内接四边形的四边长为 ,
,  ,
,  ,
,  ,且外切于圆
,且外切于圆 ,则其面积为:
,则其面积为:

由于四边形内接于圆 ,所以:
,所以:

其中p为半周长:

又因为四边形外切圆 ,所以:
,所以:

则:

同理:
 ,
,
 ,
,

综上:

证毕。
对一般四边形的面积有布雷特施奈德公式,其叙述如下:

其中  是四边形一对对角和的一半。
是四边形一对对角和的一半。
注意到不论取到哪一对对角  的值都一样,因为四边形的内角和是
的值都一样,因为四边形的内角和是  ,故如果选取到的是另一对角,其对角和的一半是
,故如果选取到的是另一对角,其对角和的一半是  。而
。而  ,所以有
,所以有  。
。
假设此时四边形恰好四顶点共圆,由于圆内接四边形的对角和为  ,因此
,因此  ,而且由
,而且由  ,可推得此时
,可推得此时  ,布雷特施奈德公式恰好退化回婆罗摩笈多公式。
,布雷特施奈德公式恰好退化回婆罗摩笈多公式。
另一个由柯立芝所证明的公式如下[1]:

其中 及
及 为四边形对角线之长。在圆内接四边形中,根据托勒密定理我们有
为四边形对角线之长。在圆内接四边形中,根据托勒密定理我们有 ,此公式退化回为婆罗摩笈多公式。
,此公式退化回为婆罗摩笈多公式。
海伦公式给出三角形的面积。它是婆罗摩笈多公式取 的特殊情形。
的特殊情形。
婆罗摩笈多公式的基本形式和扩充形式,就像由勾股定理扩充至余弦定理一般。
- ^ J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) pp. 345-347.





























![{\displaystyle =[(p+q)^{2}-(r-s)^{2}][(r+s)^{2}-(p-q)^{2}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/389f3fb3ec2407821704c894329c2981798621ed)





























