中心距 (食)
外观
(重定向自伽瑪 (食))
中心距(符号为γ)是描述中心食的月球或地球的阴影如何碰触到对方,是影锥轴线最接近地球或月球的中心时的距离,并以地球的赤道半径为单位表示其值。对日食,γ值正或负的定义是月球阴影的轴通过地球中心的北侧或南侧时,最接近的位置在北边时是正值。所谓地球中心,指曝露在太阳那一侧地球半球的中心,也就是太阳在头顶上方的点。那与地球的赤道或极点无关,因此会随着季节改变。对月食,γ值正或负的定义是地影的轴线通过月球中心的北侧或南侧时,最接近的位置在南边时是正值。
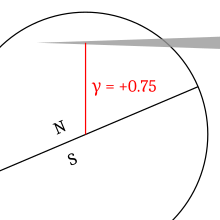
毗邻的关系图说明日食的中心距(γ):红线显示最接近地球中心的距离,在这个例子中大约是地球半径的75%。因为本影经过地球中心的北方,所在这个例子的γ是+0.75。
- 如果中心距是0,影锥是经过地球朝向太阳那一面的中心点,在南半部和北半部是完全均等。
- 如果中心距低于0.9972,则食是中心食。影锥的轴会经过地球,在其经过的地点会看见月球在太阳中心的前方。中心食可以是全食或环食(如果影锥的尖端刚刚好可以或多或少的碰触到地球的表面,则食的类型会改变,会从环食开始,中段是全食,然后再以环食结束,这种称为混合日食)。
如果地球是一个理想球体,中心食的限制应该是1.0,但是因为地球是扁圆形,所以成为0.9972[3]
2014年4月29日日食的中心距是1.0001,发生中心食是环食而不是全食的特殊情况。影锥的轴心似有若无的几乎没有碰触到地球的南极地区,因而发生非中心食的环食[4]。
相关条目
[编辑]参考资料
[编辑]- ^ J. Meeus: Astronomical Algorithms. 2nd ed., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Chapter 54
- ^ The radius of penumbra of the Moon in the fundamental pane is about 0.53 to 0.57 of the Earth's radius.
J. Meeus: Mathematical Astronomy, Morsels, Willmann-Bell, 2000, ISBN 0-943396-51-4, Fig. 10.c. und
J. Meeus: Mathematical Astronomy, Morsels III, Willmann-Bell, 2004, ISBN 0-943396-81-6, Page 46 - ^ J. Meeus: Mathematical Astronomy Morsels III. Willmann-Bell, Richmond 2004, ISBN 0-943396-81-6, Chapter 6
- ^ Fred Espenak: Path of the Annular Solar Eclipse of 2014 Apr 29 (页面存档备份,存于互联网档案馆)



