事件视界

事件视界(英语:event horizon),亦称事件穹界,是一种时空的曲隔界线。
视界中任何的事件皆无法对视界外的观察者产生影响,在黑洞周围的便是事件视界。
在非常巨大的重力影响下,黑洞附近的逃逸速度大于光速,使得任何光线皆不可能从事件视界内部逃脱。
根据广义相对论,在远离视界的外部观察者眼中,任何从视界外部接近视界的物件,将需要用无限长的时间到达视界面,其影像会经历无止境逐渐增强的红移;但该物件本身却不会感到任何异常,并会在有限时间之内穿过视界。
阿赫麦德·阿姆黑利(Ahmed Almheiri)、唐纳德·马若夫(Donald Marolf)、约瑟夫·波尔钦斯基(Joseph Polchinski)、詹姆斯·苏利(James Sully)近年的研究认为事件视界会造成黑洞火墙,而火墙的存在跟黑洞本身相矛盾。[1]
其他相关但不同的视界包括同样可以在黑洞旁找到的绝对视界线与视视界。另有一些相关的名词包括柯西与基林视界、 克尔度规中的能层、宇宙学中的宇宙学视界等。
黑洞的事件视界
[编辑]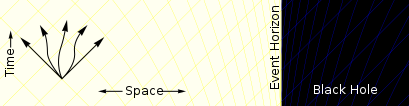 远离黑洞的粒子可以随意地向各方向移动,仅仅有光速为其速度上限这一限制。 |
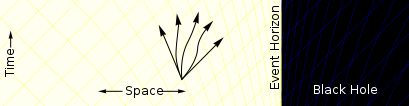 时空在靠近黑洞的地方开始变形。在一些坐标系中,向黑洞移动的路径多过于远离黑洞的路径。[Note 1] |
 在事件视界中所有的路径都是朝向黑洞中心,没有粒子可以脱离。 |
事件视界最有名的例子来自于广义相对论中对于黑洞的描述:一个质量大到附近的物质或辐射无法逃离其重力场的天体。通常,这个边界是当对于黑洞的脱离速度大于光速的位置。然而,更精确的描述是在这个视界中,所有的光锥都已经变形朝向黑洞中心。一旦粒子进入视界中,朝向黑洞运行与在时间中前行时一样不可避免的,而两者在某些坐标系底下甚至是一样的。[3][4]
大小为史瓦西半径的物体表面便是一个不转动的黑洞的事件视界(转动的黑洞的行为稍有不同)。一个物体的史瓦西半径正比于其质量。理论上来说,任何有质量的物体都可以被压缩成一个黑洞,只要我们将所有的质量压缩进其对应的史瓦西半径大小的空间中。例如太阳的史瓦西半径大约是3公里长,而地球的史瓦西半径约为9毫米。[5]然而实际上来说,地球与太阳都不具备足够大的质量来抵抗如此高密度的情形下产生的电子与中子简并压力。要克服这样的压力而形成黑洞所需要的质量称之为奥本海默极限,大约需要至少3倍于太阳的质量。[6]
然而,与黑洞事件视界的观念常常被误解。人们通常错误地认为黑洞会将物质抽入真空,实际上黑洞对于物质的吸引力与其他具有重力的物质皆一样。另外一个常常被误解的概念是认为人们可以观测到物质掉入黑洞的过程,这却是不可能的。天文学家仅仅可以看到黑洞附近的吸积盘,因为这里物质高速运动所产生的高能辐射可以被人们观测。另外,遥远的观测者并不可能看到物质跨越事件视界,而仅仅能看到物质以越来越慢的速度靠近它。[3]
宇宙学视界
[编辑]在宇宙学中也有不同的视界。其中宇宙学的事件视界是位于可观测宇宙中同移距离最远处,也就是“现在”所放出的光子将能被未来的观测者看到的最远距离处。[7]这与另外一个宇宙学中的视界,粒子视界,的观念是不同的。粒子视界是在给定某个时间的观测者后,过去释放的粒子仍旧能到达这个观测者的最远同移距离处。在粒子视界更远处,即便是宇宙刚诞生时就发出的光子将不能再到达这个观测者。[8] 而宇宙学视界的位置与时间的关系是根据宇宙膨胀所决定的。当宇宙的膨胀具备特定的性质,无论观测者等待多久时间,部分的宇宙将永远无法被观测。
在这个公式中,""是宇宙标度因子、""是光速、""是时空坐标系时间轴的重点,若宇宙永远膨胀下去,则这个值为无限大。
然而也有宇宙学的模型是没有事件视界存在的,一个例子便是德西特宇宙模型。 关于宇宙学视界具体的计算被详细的记录在关于FLRW宇宙学模型的论文中,一个以状态方程近似宇宙的模型。[8][10]
加速粒子的相对视界
[编辑]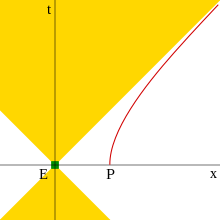
若一个粒子在不膨胀的宇宙中以等速移动且不受到重力场作用,那么那个宇宙中发生的任何事件将终究被这个粒子所看到,因为这些事件前方的光锥与粒子的世界线有所交集。
另一方面,若粒子在加速运动,某些情况下事件的光锥并不会与粒子的世界线有所交集。
在这样的情况下,我们说一个相对视界出现在粒子的(加速)参考坐标系中,代表着一个事件无法被粒子观测到的边界。
例如说,一个等加速度运动的粒子便会有相对视界。
右图展示了这个情况的一个示意图。当一个粒子加速时,他会越来越接近光速,但并无法相对于他自己的参考坐标系达到光速。
图中,他的轨迹是一个双曲线,而双曲线的渐近线是一条45度的直线。
若一个事件的光锥的边缘是在这个渐近线以内的话那他便无法被这个粒子所观测。
从粒子的角度来说,那里便形成了一个没有讯号可以逃出的边界,称之为相对视界。
在日常生活中视界并不会出现,因为这需要无限地加速粒子,也就代表我们需要无限的能量以及无限大的器材。
与事件视界的相互作用
[编辑]人们常常认为事件视界,特别是黑洞的事件视界是一个会摧毁接近其物质的不可变界面。
实际上,所有事件视界的观念都是对于远离其的观测者来说的,接近事件视界的物体则自身从不会感受到自己跨越了事件视界(也就是跨越视界这个事件的光锥和观测者的世界线永不相交)。[11]
对于一个在宽广空间以等加速度运动的观测者来说,无论周围的物质如何移动,视界看起来都在一个固定的距离外。若是改变观测者的加速度则视界的位置便可能有所变动。
另外,观测者永远不会碰触到视界也不会跨越视界。[3]若观测者是居住在德西特宇宙中的一个惯性坐标的话,那么视界的位置也将维持固定不变。[12]
当讨论的是黑洞的视界时,位处遥远且相对静止的观测者将看到处在同个位置的事件视界。
这似乎可以允许观测者降下一根绳子让他碰触事件视界,因为到视界的距离是有限的,所以仅仅需要有限长的绳子便可以达成。
实际上这却无法办到,若是缓慢的垂下绳子(也就是绳子上的每一点在史瓦西坐标中是相对静止的),越靠近视界的绳子上每一点所受到的加速度(G力)便将越趋近于无限大,于是绳子便会被撕裂。
若是快速的降下绳子,那么绳子的底端确实可以接触甚至跨越视界。
但一旦这发生了,观测者将无法再将绳子拉回,因为拉回绳子必定将会拉紧绳子,然而假设绳子是拉紧的,那么绳子上的张力将随着靠近视界的距离无限增大并在某处拉断绳子。
并且,绳子断裂的地方不会发生在事件视界上而是在一个可以被观测者所看到的地方。[13]
参见
[编辑]附注
[编辑]参考文献
[编辑]- ^ 存档副本. [2018-03-17]. (原始内容存档于2019-05-02). (页面存档备份,存于互联网档案馆)
- ^ Misner, Thorne & Wheeler 1973,第848页
- ^ 3.0 3.1 3.2 科學人雜誌-重力為什麼會影響時間?在黑洞裡時間會停止嗎?. [2017-01-16]. (原始内容存档于2019-05-02). (页面存档备份,存于互联网档案馆)
- ^ Dieter Brill, “Black Hole Horizons and How They Begin”, Astronomical Review (2012); Online Article, cited Sept.2012.. [2017-01-16]. (原始内容存档于2014-09-16). (页面存档备份,存于互联网档案馆)
- ^ 光與物質小站-什麼是黑洞的史瓦西半徑?. [2017-01-16]. (原始内容存档于2018-11-11). (页面存档备份,存于互联网档案馆)
- ^ I. Bombaci. The Maximum Mass of a Neutron Star. Astronomy and Astrophysics. 1996, 305: 871–877. Bibcode:1996A&A...305..871B.
- ^ Lars Bergström and Ariel Goobar: "Cosmology and Particle Physics", WILEY (1999), page 65.ISBN 0-471-97041-7
- ^ 8.0 8.1 Margalef-Bentabol, Berta; Margalef-Bentabol, Juan; Cepa, Jordi. Evolution of the cosmological horizons in a universe with countably infinitely many state equations. Journal of Cosmology and Astroparticle Physics. 015. 2013-02-08, 2013 (02) [2017-01-16]. Bibcode:2013JCAP...02..015M. arXiv:1302.2186
 . doi:10.1088/1475-7516/2013/02/015. (原始内容存档于2019-12-08). (页面存档备份,存于互联网档案馆)
. doi:10.1088/1475-7516/2013/02/015. (原始内容存档于2019-12-08). (页面存档备份,存于互联网档案馆)
- ^ Massimo Giovannini. A primer on the physics of the cosmic microwave background. World Scientific. 2008: 70– [2011-05-01]. ISBN 978-981-279-142-9. (原始内容存档于2019-05-02). (页面存档备份,存于互联网档案馆)
- ^ Margalef-Bentabol, Berta; Juan Margalef-Bentabol; Jordi Cepa. Evolution of the cosmological horizons in a concordance universe. Journal of Cosmology and Astroparticle Physics. 2012-12-21, 2012 (12): 035 [2017-01-16]. Bibcode:2012JCAP...12..035M. arXiv:1302.1609
 . doi:10.1088/1475-7516/2012/12/035. (原始内容存档于2019-12-08). (页面存档备份,存于互联网档案馆)
. doi:10.1088/1475-7516/2012/12/035. (原始内容存档于2019-12-08). (页面存档备份,存于互联网档案馆)
- ^ UCSB ScienceLine - What happens beyond an event horizon?. [2017-01-16]. (原始内容存档于2020-11-11). (页面存档备份,存于互联网档案馆)
- ^
Berestovskii, Valera; Irina Zubareva. Correct observer's event horizon in de Sitter space-time. arXiv:1406.3239
 .
.
- ^ Charles Misner, Kip Thorne, and John Wheeler (1973). Gravitation, p. 824
延伸阅读
[编辑]- 史蒂芬·霍金. 果壳中的宇宙. 大块文化. 2001.
- 基普·索恩. 黑洞与时间弯曲. 湖南科学技术出版社. 2000.
- Abhay Ashtekar and Badri Krishnan, “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, (2004), 10; Online Article, cited Feb.2009.[失效链接]







