八面體
外观
| 部分的八面體 | |
|---|---|
 異相雙三角柱 |
 六角柱 |
 正八面體 |
 截角四面體 |
在幾何學中,八面體是指由八個面組成的多面體,而由八個全等的正三角形組成的八面體稱為正八面體。其中正八面體是八面體中頂點和邊數最少的多面體,一些八面體可能有超過12個頂點和18條邊[1]。在八面體中亦有一種星形多面體,即星形八面體[2] 。
在許多情況下,常用「八面體」一詞來代表正八面體。
命名
[编辑]雖然具有8個面的多面體,都稱為八面體。然而,“八面體”這個幾何術語,主要是指正八面體,其中有8個三角形面。一般提到“八面體”都會聯想到正八面體,但都忽略掉最原始的定義:凡是由八個面所組成的多面體皆稱為八面體。
凸八面體
[编辑]在所有凸八面體當中,拓樸結構有明顯差異的凸八面體,包含其鏡射像共有257種[3]。其中有2種具有6個頂點、11種具有7個頂點、42種具有8個頂點、74種具有9個頂點、76種具有10個頂點、38種具有11個頂點和14種具有12個頂點的凸八面體[4]。
常見的八面體
[编辑]常見的八面體有正八面體、六角柱、七角錐、截角四面體、正三角帳塔、異相雙三角柱、側錐三角柱、三角反稜柱等。
詹森多面體
[编辑]有3種詹森多面體具有8個面。
| 名稱 | 種類 | 圖像 | 編號 | 頂點 | 邊 | 面 | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|
| 正三角帳塔 | 帳塔 | 
|
J3 | 9 | 15 | 8 | 4個正三角形 3個正方形 1個正六邊形 |
C3v, [3], (*33) | 
|
| 異相雙三角柱 | 柱體的組合 | 
|
J26 | 8 | 14 | 8 | 4個正三角形 4個正方形 |
D2d | 
|
| 側錐五角柱 | 錐體與柱體組合 | 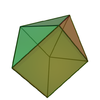
|
J49 | 7 | 13 | 8 | 6個正三角形 2個正方形 |
C2v | 
|
六角柱
[编辑]六角柱又稱六角稜柱[5],是一種底面為六邊形的柱體[6]。所有六角柱都有8個面,18個邊和12個頂點[7]。正六角柱代表每個面都是正多邊形的六角柱,其每個頂點都是2個正方形和1個正六邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正八面體。
七角錐
[编辑]七角錐是一種底面為七邊形的錐體,其具有7個面、14條邊和7個頂點,其對偶多面體是自己本身。正七角錐是一種底面為正七邊形的七角錐。
八面體列表
[编辑]| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
| 正八面體 | 正多面體 | 
|
{3,4} |
6 | 12 | 8 | 2 | 8個正三角形 |
Oh, BC3, [4,3], (*432) | 
|
| 六角柱 | 稜柱體 | 
|
t{2,6} {6}x{} |
12 | 18 | 8 | 2 | 2個六邊形 6個矩形 |
D6h, [6,2], (*622), order 24 | 
|
| 三角反棱柱 | 反稜柱 | 
|
s{2,3} | 6 | 12 | 8 | 2 | 2個三角形底面 6個三角形側面 |
D3d, [2+,6], (2*3), order 12 | |
| 七角錐 | 稜錐體 | 
|
( )∨{5} | 8 | 14 | 8 | 2 | 1個七邊形 7個三角形 |
C7v, [7], (*77) |
參見
[编辑]參考文獻
[编辑]- ^ Enumeration of Polyhedra. UW Green Bay. 1997-09-23 [2016-08-14]. (原始内容存档于2011-10-10).
- ^ Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, 1987. ISBN 978-0486253572
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Polyhedra with 8 Faces and 6-8 Vertices. UW Green Bay. 1997-09-23 [2016-08-14]. (原始内容存档于2014-11-17).
- ^ hexagonal prism. 國家教育研究院. [2016-08-17]. (原始内容存档于2016-08-17).
- ^ hexagonal prism. Maths A to Z. School A to Z. [2016-08-17]. (原始内容存档于2016-08-17).
- ^ Pugh, Anthony, Polyhedra: A Visual Approach, University of California Press: 21, 27, 62, 1976 [2016-08-18], ISBN 9780520030565, (原始内容存档于2014-07-09).
