自由膨脹

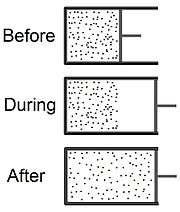
自由膨脹（英語：free expansion）也稱為焦耳膨脹，是一種不可逆的熱力學過程，過程中氣體在一個絕熱的系統內，一開始氣體只在系統的部份區域，和其他部份用隔板隔開，之後突然移除隔板，使氣體膨脹，外界和系統之間沒有功和熱的交換。

自由膨脹是一個有關理想氣體的思想實驗，可以探討古典熱力學的現象。這個例子可以用來計算熱力學物理量的變化，包括因為此過程的不可逆，造成整體熵的增加（熵產生量（英語：entropy production））。針對理想氣體的自由膨脹，過程前後的溫度不會變化，而且過程前後的狀態符合以下的式子

p_i V_i = p_f V_f,

其中p為壓力，V為體積而下標的i及f表示初始及結束的狀態。

實際的自由膨脹會和實際氣體的特性有關，這類過程中的溫度變化可以量測分子間作用力。

焦耳膨脹的名稱是得名自詹姆斯·焦耳，他在1845年研究功和熱時有使用膨脹，但此過程在焦耳之前就已為人所知，例如約翰·萊斯利在19世紀初就已知道，約瑟夫·路易·給呂薩克在1807年也研究，得到和焦耳類似的結果^[1]^[2]。

說明

此過程開始於某壓力 $P_{\mathrm {i} }$ 、某溫度 $T_{\mathrm {i} }$ 的氣體，限制在某隔熱（英語：Thermal contact）容器中的一半空間（可參考此條目最上方的圖）。氣體的初始體積為 $V_{\mathrm {i} }$ ，和容器的另一半空間（體積 $V_{\mathrm {0} }$ ）已用機構隔開, 而另一半空間的壓力是零。若兩半空間之間的分隔突然移除，氣體會膨脹充滿整個容器，其總體積是 $V_{\mathrm {f} }=V_{\mathrm {i} }+V_{\mathrm {0} }$ 。在容器的左半邊有插入溫度計，量測膨脹前後的氣體熱力學溫度。

這個實驗的熱力學系統包括容器的兩個半邊，也就是實驗結束時氣體所充滿的空間。因為系統隔熱，無法和周圍交換熱量。因為總體積不變，外界也無法對系統作功^[3]。因此，內能變化 $\Delta U$ 為零。內能包括內部的動能（因為分子移動）以及內部位能（因為分子間作用力）。當分子隨機運動時，溫度是對內部動態的量測。此例中，內部動態即為熱。若腔室沒有達到平衡，會有動能的流動，這部份是溫度計無法偵測的（因此不是熱的成份之一）。因此，溫度的變化表示動能的變化，一直要到重新達到熱平衡，才能完全看到此變化。當熱以動能流動的方式傳輸，會讓溫度下降^[4]。實務上，簡單的兩腔室自由膨脹常會加入多孔塞，膨脹的氣體需通過多孔塞才能到低壓的腔室。此目的是為了禁止方向性的流動，加快熱平衡的重新建立。因為總內能沒有變化，腔室中的停滯流讓動能又轉換為氣體的隨機運動（熱），因此溫度會上昇到預期溫度。若初始空氣壓力夠低，讓非理想氣體成份凝結，一些內能會轉換為液體的潛熱（位能的變化）。因此，低溫下的自由膨脹提供了分子間作用力的資訊。

理想氣體

若是理想氣體，其初始狀態（ $T_{\mathrm {i} }$ , $P_{\mathrm {i} }$ , $V_{\mathrm {i} }$ ）和最終狀態（ $T_{\mathrm {f} }$ , $P_{\mathrm {f} }$ , $V_{\mathrm {f} }$ ）會依照理想氣體定律，一開始時 $P_{\mathrm {i} }V_{\mathrm {i} }=nRT_{\mathrm {i} }$ 隔板打開後 $P_{\mathrm {f} }V_{\mathrm {f} }=nRT_{\mathrm {f} }.$

此處 $n$ 是氣體莫耳數， $R$ 是莫耳理想氣體常數。因為內能沒有變化，而理想氣體的內能只是溫度的函數，因此溫度沒有變化， $T_{\mathrm {i} }=T_{\mathrm {f} }$ 。這表示 $P_{\mathrm {i} }V_{\mathrm {i} }=P_{\mathrm {f} }V_{\mathrm {f} }=nRT_{\mathrm {i} }.$

若體積加倍，壓力會減半。

溫度不會變化的事實，方便計算整體熵的變化。

真實氣體

真實氣體的自由膨脹和理想氣體不同，真實氣體自由膨脹後，溫度會變化。若溫度比反轉溫度（英語：inversion temperature）（inversion temperature）要低，氣體在自由膨脹後會降溫，若溫度比反轉溫度高，在自由膨脹後，氣體溫度會上昇^[5]^[6]。一般來言，氣體的反轉溫度會高於室溫，只有氦氣（反轉溫度約40 K）和氫氣（反轉溫度約200 K）例外。因為自由膨脹過程中，內能是定值，自由膨脹過程中的降溫是因為內部動能轉換為位能，昇溫則是內部位能轉換為動能。

參考資料

大部份大學教科書都對此主題說明的很深入，例如Concepts in Thermal Physics, Blundell & Blundell, OUP ISBN 0-19-856770-7

^ D.S.L. Cardwell, From Watt to Clausius, Heinemann, London (1957)
^ M.J. Klein, Principles of the theory of heat, D. Reidel Pub.Cy., Dordrecht (1986)
^ 氣體是否在真空中膨脹其實並不重要，若右半邊不是完全真空，有低壓氣體，系統對環境作的功也是零。此時，氣體有對右半邊的氣體作功，但沒有對環境作功
^ V.A. Kirillin, et al, Engineering Thermodynamics,(1981) Mir Publishers, Chapter 7.7 p.265
^ Goussard, J.-O.; Roulet, B. Free expansion for real gases. Am. J. Phys. 1993, 61 (9): 845–848. Bibcode:1993AmJPh..61..845G. doi:10.1119/1.17417.
^ Albarrán-Zavala, E.; Espinoza-Elizarraraz, B.A.; Angulo-Brown, F. Joule inversion temperatures for some simple real gases. The Open Thermodynamics Journal. 2009, 3: 17–22. doi:10.2174/1874396x00903010017 .

[1] D.S.L. Cardwell, From Watt to Clausius, Heinemann, London (1957)

[2] M.J. Klein, Principles of the theory of heat, D. Reidel Pub.Cy., Dordrecht (1986)

[3] 氣體是否在真空中膨脹其實並不重要，若右半邊不是完全真空，有低壓氣體，系統對環境作的功也是零。此時，氣體有對右半邊的氣體作功，但沒有對環境作功

[4] V.A. Kirillin, et al, Engineering Thermodynamics,(1981) Mir Publishers, Chapter 7.7 p.265

[:0-5] Goussard, J.-O.; Roulet, B. Free expansion for real gases. Am. J. Phys. 1993, 61 (9): 845–848. Bibcode:1993AmJPh..61..845G. doi:10.1119/1.17417.

[:1-6] Albarrán-Zavala, E.; Espinoza-Elizarraraz, B.A.; Angulo-Brown, F. Joule inversion temperatures for some simple real gases. The Open Thermodynamics Journal. 2009, 3: 17–22. doi:10.2174/1874396x00903010017 .

[1]

[2]

[3]

[4]

[5]

[6]

說明

理想氣體

真實氣體

相關條目

參考資料