著色
在電腦圖學中，著色，也稱濃淡處理、明暗處理、著色法（英語：Shading）是在三維模型或插畫中通過不同的亮度表現深度的方法。
繪圖
[編輯]
濃淡處理是用較大壓力在紙上繪製較深顏色、用較小壓力繪製較淺顏色從而表示不同明暗程度的過程。有許多不同的濃淡處理技術，其中交叉影線是用不同距離互相垂直的網格線繪製不同區域的濃淡。影線距離越近，所繪製區域越暗；相反，距離越遠，所繪製區域越亮。這個術語近來用來泛指使用濃淡工具的場合。
物體都有照亮區域以及陰影區域這樣不同的光照模式，這種現象可以用於在紙上以及計算機屏幕上顯示不同的深度。
計算機圖形學
[編輯]在計算機圖形學中，濃淡處理表示根據物體相對於光線的角度及其與光源的距離改變物體明暗生成photorealistic效果的過程。濃淡處理是在渲染過程中的一步，由著色器完成。
光照模型
[編輯]濃淡處理的算法因光源種類而異。 通常來說多種效果會在一起使用，以增加場真實性。因為不同類型的光源會效果不一。
環境光
[編輯]環境光光源是一個固定強度，固定顏色的光源，他無方向無差別地作用於所有物體。所有物體都會有一樣的顏色和亮度。這樣的光源主要用於提供一個基本照明。這是最簡單的一種照明模型，也能模擬光線被多次反射散射後產生的一個均一的效果。
有向光
[編輯]有向光從一個方向無差別地照亮所有物體。就像一個無限大和無限遠的區域光源。他會在物體表面產生明暗效果， 但不會根據距離衰減。
點光
[編輯]光從一點出發，向所有方向投射。
聚光燈光
[編輯]模擬一個聚光燈。 光從錐形頂點向底部投射。
區域光
[編輯]光從平面上的一小區域發出，是比點光源更準確的模型。
有體積光
[編輯]光從一個有體積的小物體發出。
相對於光源的角度
[編輯]除了環境光以外，其他光都是有方向性的。根據物體表面和光線的夾角不同，濃淡處理算法會改變三維模型中的表面顏色和明暗程度。
下面的第一張圖中的盒子的每個表面都用同一種顏色進行渲染，畫出邊線是為了易於觀看。
第二張圖是同一張模型，但是沒有繪製邊線。我們很難分辨出這張圖的每一個表面。
第三種進行了濃淡處理，這樣圖像看起來更加真實，也易於分辨每個表面。
-
盒子的渲染圖像，沒有進行濃淡處理，但是繪製了邊線以分割表面 -
同第一幅圖像一樣，但是沒有繪製邊線 -
同一模型根據三個表面相對於光源的角度進行了濃淡處理得到的圖像
距離衰減
[編輯]理論上講，如太陽這樣的遠距離光源對於兩個平行表面的的照明亮度是一樣的，儘管其中一個表面可能較遠，但亮度仍然看起來是一樣的。
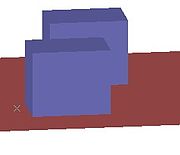
注意在第一幅圖中，兩個盒子正面的顏色是完全相同的。但是在兩個表面相交的地方看起來顏色有些差別，這是因為在兩個表面相交部分下面還有一段豎直邊緣帶來的視覺幻覺。
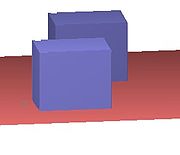
在第二幅圖中，前面盒子的正面比後面盒子的正面要亮，並且地板也從前到後逐漸變暗。
這種 距離衰減 效果生成的圖像看起來更加真實，並且不需要添加額外的照明來實現同樣的效果。
-
使用OpenGL渲染工具生成的兩個盒子 -
用ARRIS CAD渲染的同一模型，它實現了「Distance Falloff」從而距離較近的表面看起來更加明亮
距離衰減的計算可以有以下幾種算法
- 無 - 光強跟點於光源之間的距離無關。
- 線性 - 光強正比於距離的倒數。
- 二次 - 光強正比於距離倒數的平方。這是在無霧或其他東西吸收或者散射的情況下光強的真實衰減模型。
- n階 - 光強正比於距離倒數的n次方。
- 其他計算方式也可以
插值技術
[編輯]
渲染過程中需要計算表面的亮度，上述光照模型要求我們提前知道表面上任意點的法線。然而，三維模型一般都是通過多邊形網格描述的，只能在有限的點存儲法線，這些點通常是多邊形的頂點。為了解決這一問題，可以使用不同的插值技術。
平直著色法
[編輯]平直著色法（英語：flat shading）基於「組成模型的多邊形都是平的」的假設，認為在同一多邊形上任意點的法線都相同。
使用這種著色法時，先在每個多邊形上挑選一個點計算顏色（通常是多邊形的第一個頂點，如果是三角形網格則也可以選擇幾何中心），則該多邊形上其餘點都直接使用該點的顏色。所以，使用平直著色法的每個多邊形上都是統一的顏色，和最近鄰插值的效果類似。
其它更加高級的著色技術由於計算量太大不便於使用時，這種方法經常用於高速渲染。由於每個多邊形都是統一的顏色，所以使用這種著色法也更易於區分相鄰的多邊形。但這種著色法很難做出高光效果：一個表面要不全高光，要不全沒有，因此高光模型很少使用在這個著色方法中。
平滑著色法
[編輯]使用平直著色法時，顏色在多邊形的邊緣跳變。而使用平滑著色法（英語：smooth shading）時，每個像素的顏色都可以不同，相鄰多邊形之間的顏色轉變看上去就比較平滑。通常先計算多邊形頂點的顏色，再通過雙線性插值來確定多邊形上其它點的像素值。
常見的平滑著色包括：
- Gouraud著色法 [3]
- Phong著色法 [4]
此外，還有通過泰勒級數展開[1]、球面線性插值[2]等方法實現的平滑著色法。
Gouraud著色法
[編輯]- 計算多邊形的頂點法向量
- 用光照模型去計算每個頂點的光強
- 用雙線性插值計算多邊形表面上每個像素的明暗
有時頂點法向量能被直接計算（如均一網格上的高度圖）。更一般來說我們需要一個有效的資料結構，能快速找到哪些多邊形共用這個頂點。
Gouraud著色法的優勢在於，即便是比三角形複雜的多邊形，每個頂點也可以有不一樣的顏色，內部插值算法可以更多變。
而Gouraud著色法也有一些問題：
- 鄰接多邊形可能有不一樣的顏色。
- Gouraud著色 需要比較大的CPU計算量，在實時處理大量多邊形時可能會成為問題。
- 3個多邊形邊的T型連接可能會被錯誤的繪製，一般來說應該避免存在T型連接
Phong著色法
[編輯]Phong著色法與Gouraud著色法類似，區別在於進行雙線性插值的不是光照強度本身，而是頂點的法線。因此使用這種著色法計算出的高光比Gouraud著色更精確。
- 計算多邊形頂點的法向量
- 雙線性插值計算每個像素點的法向量
- 通過每個像素的法向量計算光強
- 根據光強繪製像素
平直著色與平滑著色對比
[編輯]| 平直著色 | 平滑著色 |
|---|---|
| 一個面的所有像素用同一種顏色，一般是第一個頂點的顏色 | 對頂點的顏色進行插值運算，每個像素不一樣 |
| 邊比真實物體更明顯lateral inhibition | 邊看不見 |
| 繪製出每個平面 | 繪製出光滑曲面 |
| 不適合光滑物體 | 適合光滑物體 |
| 計算量少 | 計算量大 |
