粒子衰變

粒子衰變是一基本粒子變成其他基本粒子的自發過程。在這個過程中，一基本粒子變成質量更輕的另一種基本粒子，及一中間粒子，例如緲子衰變中的W玻色子。這中間粒子隨即變成其他粒子。如果生成的粒子不穩定，那麼衰變過程還會繼續。

粒子衰變這種過程，與放射性衰變不一樣，後者為一不穩定的原子核，變成一更小的原子核，當中還伴隨着粒子或輻射的發射。

注意本條目使用自然單位，即

$c=\hbar =1$。

粒子壽命列表

所有數值均來自粒子數據小組：

種類	名稱	符號	能量 (MeV)	平均壽命
輕子	電子 / 正電子	$e^{-}\,/\,e^{+}$	0.511	$>4.6\times 10^{26}$ 年
	緲子 / 反緲子	$\mu ^{-}\,/\,\mu ^{+}$	105.6	$2.2\times 10^{-6}$ 秒
	陶子 / 反陶子	$\tau ^{-}\,/\,\tau ^{+}$	1777	$2.9\times 10^{-13}$ 秒
介子	中性π介子	$\pi ^{0}\,$	135	$8.4\times 10^{-17}$ 秒
	帶電π介子	$\pi ^{+}\,/\,\pi ^{-}$	139.6	$2.6\times 10^{-8}$ 秒
重子	質子 / 反質子	$p^{+}\,/\,p^{-}$	938.2	$>10^{29}$ 年
	中子 / 反中子	$n\,/\,{\bar {n}}$	939.6	$885.7$ 秒
玻色子	W玻色子	$W^{+}\,/\,W^{-}$	80,400	$10^{-25}$ 秒
	Z玻色子	$Z^{0}\,$	91,000	$10^{-25}$ 秒

生還機率

把一粒子的平均壽命標記為$\tau$，這樣粒子在時間t後仍生還（即未衰變）的機率為

$P(t)=e^{-t/(\gamma \tau )}$

其中

$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$為該粒子的勞侖茲因子。

衰變率

設一粒子質量為M，則衰變率可用下面的通用公式表示

$d\Gamma _{n}={\frac {(2\pi )^{4}}{2M}}\left|{\mathcal {M}}\right|^{2}d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})$

其中

n為原衰變所生成的粒子數，

${\mathcal {M}}\,$為連接始態與終態的不變矩陣上的元，

$d\Phi _{n}\,$ 為相空間的元，及

$p_{i}\,$為粒子i 的四維動量。

相空間可由下式所得，

$d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})=\delta ^{4}(P-\sum _{i=1}^{n}p_{i})\left(\prod _{i=1}^{n}{\frac {d^{3}{\vec {p}}_{i}}{(2\pi )^{3}2E_{i}}}\right)\,$

其中

$\delta ^{4}\,$為四維的狄拉克δ函數。

三體衰變

作為例子，一粒子衰變成三粒子時的相空間元如下：

$d\Phi _{3}={\frac {1}{(2\pi )^{9}}}\delta ^{4}(P-p_{1}-p_{2}-p_{3}){\frac {d^{3}{\vec {p}}_{1}}{2E_{1}}}{\frac {d^{3}{\vec {p}}_{2}}{2E_{2}}}{\frac {d^{3}{\vec {p}}_{3}}{2E_{3}}}\,$

四維動量

主條目：四維動量

一粒子的四維動量又叫其不變質量。

一粒子的四維動量平方，定義為其能量平方與其三維動量平方間的差（注意從這開始，採用的單位都能滿足光速等於1這項條件）：

$p^{2}=E^{2}-({\vec {p}})^{2}=m^{2}\quad \quad \quad \quad (1)\,$

兩粒子的四維動量平方為

$p^{2}=\left(p_{1}+p_{2}\right)^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}p_{2}=m_{1}^{2}+m_{2}^{2}+2(E_{1}E_{2}-{\vec {p}}_{1}\cdot {\vec {p}}_{2})\,$。

四維動量守恆

在所有衰變及粒子相互作用中，四維動量都必須守恆，因此始態p_i 與終態p_f 的關係為

$p_{\mathrm {i} }=p_{\mathrm {f} }$。

在二體衰變中

設母粒子質量為M，衰變成兩粒子（標記為1和2），那麼四維動量的守恆條件則為

$p_{M}=p_{1}+p_{2}$。

整理可得，

$p_{M}-p_{1}=p_{2}$

然後取左右兩邊的平方

$p_{M}^{2}+p_{1}^{2}-2p_{M}p_{1}=p_{2}^{2}$。

現在要用的正是四維動量的定義——方程式(1)，展開各p² 得

$M^{2}+m_{1}^{2}-2\left(E_{M}E_{1}-{\vec {p}}_{M}\cdot {\vec {p}}_{1}\right)=m_{2}^{2}.\quad \quad \quad \quad (2)\,$

若進入母粒子的靜止系，則

• ${\vec {p}}_{M}=0\,$，及
• $E_{M}=M\,$

將上述兩式代入方程式(2)得：

$M^{2}+m_{1}^{2}-2ME_{1}=m_{2}^{2}.\,$

整理後得粒子1於母粒子靜止系中的能量公式，

$E_{1}={\frac {M^{2}+m_{1}^{2}-m_{2}^{2}}{2M}}.\quad \quad \quad \quad (3)\,$

同樣地，粒子2在母粒子在靜止系中的能量為

$E_{2}={\frac {M^{2}+m_{2}^{2}-m_{1}^{2}}{2M}}$。

可得

$|{\vec {p}}_{1}|=|{\vec {p}}_{2}|={\frac {\sqrt {\left[M^{2}-\left(m_{1}+m_{2}\right)^{2}\right]\left[M^{2}-\left(m_{1}-m_{2}\right)^{2}\right]}}{2M}}.\,$

先把$E_{1}^{2}=m_{1}^{2}+{\vec {p}}_{1}^{2}\,$ 代入方程式(3)：

${\vec {p_{1}}}^{2}={\frac {(M^{2}+m_{1}^{2}-m_{2}^{2})^{2}-4m_{1}^{2}M^{2}}{4M^{2}}}\,$

${\vec {p_{1}}}^{2}={\frac {M^{4}+m_{1}^{4}+m_{2}^{4}-2m_{1}^{2}M^{2}-2m_{2}^{2}M^{2}-2m_{1}^{2}m_{2}^{2}}{4M^{2}}}\,$

${\vec {p_{1}}}^{2}={\frac {M^{4}-M^{2}(m_{1}+m_{2})^{2}-M^{2}(m_{1}-m_{2})^{2}+(m_{1}^{2}-m_{2}^{2})^{2}}{4M^{2}}}\,$

${\vec {p_{1}}}^{2}={\frac {M^{2}\left[M^{2}-(m_{1}-m_{2})^{2}\right]-(m_{1}+m_{2})^{2}\left[M^{2}-(m_{1}-m_{2})^{2}\right]}{4M^{2}}}\,$

$|{\vec {p}}_{1}|={\frac {\sqrt {\left[M^{2}-\left(m_{1}+m_{2}\right)^{2}\right]\left[M^{2}-\left(m_{1}-m_{2}\right)^{2}\right]}}{2M}}.\,$

$|{\vec {p}}_{2}|\,$的推導也一樣。

二體衰變

在質心系中，看起來靜止的母粒子衰變成兩相同質量的粒子，造成它們在夾角為180°的情況下發射。

...而在實驗室系中，母粒子大概以接近光速的速度移動，因此所發射的兩粒子，其角度會與質心系的不一樣。

從兩個不同的參考系

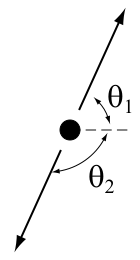
在實驗室系中發射粒子的角度，與質心系時的關係由下式表示：

$\tan {\theta '}={\frac {\sin {\theta }}{\gamma \left(\beta /\beta '+\cos {\theta }\right)}}$

衰變率

設一母粒子質量為M ，衰變成兩粒子，標記為1和2。那麼在母粒子的靜止系中，

$|{\vec {p}}_{1}|=|{\vec {p_{2}}}|={\frac {[(M^{2}-(m_{1}+m_{2})^{2})(M^{2}-(m_{1}-m_{2})^{2})]^{1/2}}{2M}}$。

另外，用球座標表示則為

$d^{3}{\vec {p}}=|p|^{2}\,dpd\Omega =p^{2}\,d\phi \,d\left(\cos \theta \right)$。

已知二體衰變的相空間元（見上文#衰變率一節，n=2），得母粒子參考系中的衰變率為：

$d\Gamma ={\frac {1}{32\pi ^{2}}}\left|{\mathcal {M}}\right|^{2}{\frac {|{\vec {p}}_{1}|}{M^{2}}}\,d\phi _{1}\,d\left(\cos \theta _{1}\right)$。

另見

• 粒子物理學
• 粒子列表
• 弱相互作用

參考資料

• J.D. Jackson. Kinematics (PDF). Particle Data Group. 2010 [2011-08-24]. （原始內容 (PDF)存檔於2021-03-28）.  －見第2頁。
• 粒子數據小組 （頁面存檔備份，存於互聯網檔案館）
• 粒子大冒險 勞倫斯伯克利國家實驗室粒子數據小組