直角邊
外觀

對於一個直角三角形,直角邊(源自希臘字Κάθετος,複數Κάθετοι);而英文的複數是catheti,是取自拉丁文cathetus的複數,常用的解釋是"leg" ,即一個直角三角形中,形成90度的兩條相鄰的邊。而餘下的一條邊,與直角相對,稱為斜邊。又因為畢氏定理在中文常被稱為勾股定理或勾股弦定理,故在中文裏,直角邊常常被稱為股,此乃延續中國古代的稱呼。"leg"這種表達方式在多數情況之下並不常用,一般都用直角邊或一個更迂迴的說法:"位於直角的一邊"。當提及到斜邊,直角邊一般被理解為餘下的兩邊。
直角邊的比例是三角函數中正切(tan)或餘切(cot)的定義(視乎參考那一隻角)。在直角三角形中,直角邊的長度亦等於斜邊的總長度與由直角用垂線分割斜邊的線段的幾何平均數。
對於一個不等腰的直角三角形,即一個任意的直角三角形,因為它的直角邊有不同的長度,所以英文可以用"major"同"minor"來分辨。
對於等腰直角三角形,它的直角邊便是其兩腰。
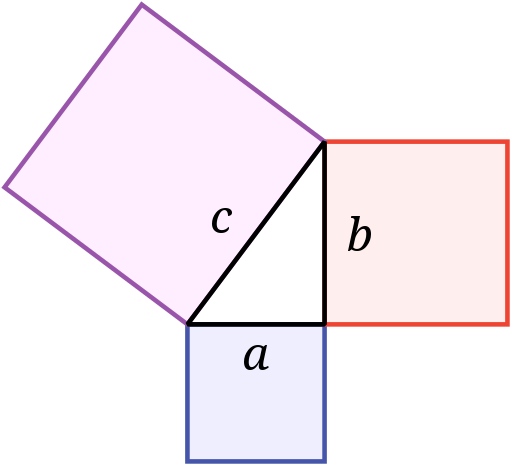
根據畢氏定理(又稱勾股定理,畢達哥拉斯定理或勾股弦定理),兩條直角邊的平方之和是等於斜邊的平方。同等地,以直角邊為邊長(見右圖)所形成的正方形(a同b),它們的平方總和等於以斜邊為邊長所形成的正方形(c)之平方和。
參考資料
[編輯]- Bernhardsen, T. Geographic Information Systems: An Introduction, 3rd ed. New York: Wiley, p. 271, 2002.
- 埃里克·韋斯坦因. Cathetus. MathWorld.
另見
[編輯]
