合力
如果一個力的作用效果和幾個力所產生的作用效果相同時,這個力就是那幾個力的合力(resultant force)。
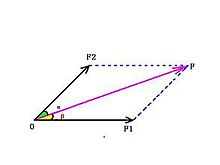
那幾個力就是這個力的分力(component force)。
如右圖,是和的合力,和是的分力。
它的另一種表述為:作用於同一物體上的多個力的向量和。所以,合力是向量。[1]
力的平衡
[編輯]合力的定義表明,任意數目的力作用在一個物體上,它們的總作用,可用它們的合力代替。
在生活中,人們經常發現,物體即使在受到外力作用時也能保持靜止或等速直線運動狀態,這似乎與牛頓第一定律相矛盾。可以運用合力來解釋這一問題。因為,當幾個力的合力使物體保持靜止或勻速直線狀態的時候。這幾個力互稱為平衡力。這個時候各個分力的作用效果互相抵消,從效果上來看,物體此時不受力。這樣,就不與牛頓第一定律相矛盾了。[2]
力的合成
[編輯]求已知幾個力的合力,稱為力的合成。
作用於同一點上的力叫做共點力,以下討論,都只在共點力的基礎上進行。
平行四邊形法則
[編輯]平行四邊形法則適用於兩個互成角度的共點力上,可以通過以下實驗證明:

如圖(a)、(b)橡皮帶GE在力和的共同作用下伸長了OE,在力的作用下,也伸長了OE。它們的作用效果相同,所以、的合力為。在力、和的方向上各做有向線段,並以一定的標度使、、的長度分別表示這三個力的大小。連接和,可以證明四邊形OABC是平行四邊形,OC是它的對角線。
經過大量實驗證明,兩個互成角度的共點力,它們的合力的大小和方向,可以用表示這兩個力的有向線段做鄰邊做畫出的平行四邊形的對角線來表示,這就是平行四邊形法則。
兩個以上的共點力合成時,也可以應用平行四邊形法則求它們的合力。方法是先求出任意兩個力的合力,再求出這個合力與第三個力的合力,這樣繼續下去,最後得出的就是這幾個多力的合力。
根據平行四邊形法則,在其他因素不改變的情況下,合力的大小與二力的夾角成反比。
力的合成的計算
[編輯]
根據平行四邊形法則,可以計算合力的具體大小和方向。
在中,通過餘弦定理,可得:
合力的方向可以用力跟的夾角表示出來。由可以求的大小
以上兩式,就是計算合力的大小與方向的公式。[3]
參考文獻
[編輯]- ^ 物理 八年级. 上海: 上海科學技術出版社. 2012: 137. ISBN 9787547812846.
- ^ 物理 八年级. 中國上海: 上海科技技術出版社. 2012: 132. ISBN 9787547812846.
- ^ 物理 上册. 中國北京: 高等教育出版社. 1985: 68. ISBN 7040017318.

















