雙穩
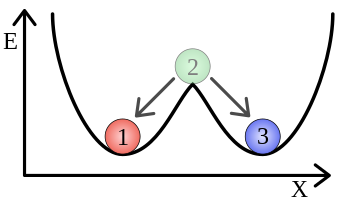
處於雙穩的系統有兩個平衡狀態。在物理學中,對於全體粒子,雙穩態源自於它的自由能有三個臨界點。其中兩個為最小值而最後一個為最大值。通過數學論證,最大值一定處於兩個最小值之間。默認情況下,系統的態將處於最小值態兩者之一,因為這樣對應於系統的最低能量。最大值可以被看作壁壘。
最低自由能態之間的躍遷,需要某些形式的激發能來穿透壁壘(對照化學裏的激發能和Arrhenius方程)。當穿越壁壘之後,系統將再一次靜止到下一個最低能態。需要的時間稱作弛豫時間(哪一個態將成為新態可能會有不確定性,但是通常情況下是被很好地定義了的)。
光學雙穩是一些光學器件的屬性, 它們往往可能有兩個諧振傳輸態,依賴於輸入的情況。
在生物和化學系統中
[編輯]雙穩態是理解細胞內某些現象作用的關鍵,比如細胞周期過程中的決策、細胞分化[1]和細胞凋亡。它也和某些事件,在早期的細胞內動態平衡的喪失相關,比如癌症的發生、阮病毒疾病甚至新物種形成(成種作用)[2]。
雙穩態的產生和具有超敏性的正反饋迴路(positive feedback loop)相關。正反饋迴路,簡單地舉例來說,X激活Y,同樣Y能激活X,從本質上來說,是將輸出信號和輸入信號聯繫在了一起。對於細胞內的信號轉導來說,這種調控形式很重要,因為它能夠產生「全或無」的開關效應[3]。研究也表明了,非常多的生物系統,比如爪蟾卵的成熟[4]、哺乳動物鈣信號的轉導和出芽酵母的極性都與(快速或者慢速)正反饋迴路相關(在不同的時間點會有多個正反饋迴路出現)[3]。如果一個系統同時擁有這兩類正反饋迴路,這樣可以(a)增加調節:兩種開關有着獨立的可變的激活或者失活時間;(b)將反饋迴路和多重時間尺度聯繫起來可以過濾噪聲[3]。
雙穩態可以被修飾地更加具有穩健性,即使體系中反應物的濃度發生很大的改變,其仍能維持着「開關」這種特性。一個細胞生物學上的例子,被激活的CDK1(Cyclin Dependent Kinase 1,細胞周期蛋白依賴的激酶1)能夠激活它的激活子Cdc25,同時CDK1也會滅活它的抑制子Wee1,這樣能夠使細胞進入有絲分裂(mitosis)。如果沒有這種雙重反饋,儘管系統仍能夠具有雙穩性,但是不能夠承受體系中反應物濃度的有較大的波動[5]。
雙穩態在果蠅胚胎發育階段中被描述過,比如頭尾軸[6]和腹背軸的形成[7][8],以及眼睛的發育[9]。
在生物系統中,和雙穩態有關的一個典型的例子是Sonic hedgehog (Shh),一種分泌的信號分子,對發育非常重要。Shh信號網絡表現為一個雙穩態的開關一樣,其濃度能夠引起細胞狀態的轉變。Shh可以激活gli1 和 gli2的轉錄,它們各自的基因產物也能夠作為轉錄激活物去促進自身和Shh信號通路下游基因的表達[10]。同時,Shh信號通路也包含一個負反饋迴路,即Gli轉錄因子能夠激活阻遏子Ptc的轉錄活性。因此,Shh信號通路中同時存在的正負反饋迴路能夠產生雙穩態開關[2]。
在生物和化學系統中,只要滿足三個條件,就能夠產生雙穩態現象:正反饋、過濾小刺激信號的機制和防止無約束增長的機制。雙穩態化學系統被廣泛地用於研究非平衡熱動力學、隨機共振和氣候變化等等[2]。在雙穩態空間擴展系統中,局部相關性的發生和旅行波的傳播曾被分析過[11][12]。
雙穩態通常可以通過滯後作用(hysteresis)來實現。從種群水平,如果將每一個個體加以考慮,在分佈上就會出現雙穩態現象。
參見
[編輯]
外部連結
[編輯]- ^ Ghaffarizadeh, Ahmadreza; Flann, Nicholas S.; Podgorski, Gregory J. Multistable switches and their role in cellular differentiation networks. BMC bioinformatics. 2014,. 15 Suppl 7: S7 [2019-01-10]. ISSN 1471-2105. PMC 4110729
 . PMID 25078021. doi:10.1186/1471-2105-15-S7-S7. (原始內容存檔於2019-01-10).
. PMID 25078021. doi:10.1186/1471-2105-15-S7-S7. (原始內容存檔於2019-01-10).
- ^ 2.0 2.1 2.2 Wilhelm, Thomas. The smallest chemical reaction system with bistability. BMC systems biology. 2009-09-08, 3: 90 [2019-01-10]. ISSN 1752-0509. PMC 2749052
 . PMID 19737387. doi:10.1186/1752-0509-3-90. (原始內容存檔於2019-01-10).
. PMID 19737387. doi:10.1186/1752-0509-3-90. (原始內容存檔於2019-01-10).
- ^ 3.0 3.1 3.2 Brandman, Onn; Ferrell, James E.; Li, Rong; Meyer, Tobias. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science (New York, N.Y.). 2005-10-21, 310 (5747): 496–498 [2019-01-10]. ISSN 1095-9203. PMC 3175767
 . PMID 16239477. doi:10.1126/science.1113834. (原始內容存檔於2019-01-10).
. PMID 16239477. doi:10.1126/science.1113834. (原始內容存檔於2019-01-10).
- ^ Ferrell, J. E.; Machleder, E. M. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science (New York, N.Y.). 1998-05-08, 280 (5365): 895–898 [2019-01-10]. ISSN 0036-8075. PMID 9572732. (原始內容存檔於2019-01-10).
- ^ Ferrell, James E. Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses. Current biology: CB. 2008-03-25, 18 (6): R244–245 [2019-01-10]. ISSN 0960-9822. PMC 2832910
 . PMID 18364225. doi:10.1016/j.cub.2008.02.035. (原始內容存檔於2019-01-10).
. PMID 18364225. doi:10.1016/j.cub.2008.02.035. (原始內容存檔於2019-01-10).
- ^ Spirov, Alexander V.; Bisch, Paulo M.; Holloway, David M.; Vieira, Fernando M. C.; Lopes, Francisco J. P. Spatial Bistability Generates hunchback Expression Sharpness in the Drosophila Embryo. PLOS Computational Biology. 2008-09-26, 4 (9): e1000184 [2020-10-03]. ISSN 1553-7358. PMC 2527687
 . PMID 18818726. doi:10.1371/journal.pcbi.1000184. (原始內容存檔於2020-07-26) (英語).
. PMID 18818726. doi:10.1371/journal.pcbi.1000184. (原始內容存檔於2020-07-26) (英語).
- ^ Ferguson, Edwin L.; Wang, Yu-Chiun. Spatial bistability of Dpp–receptor interactions during Drosophila dorsal–ventral patterning. Nature. 2005-03, 434 (7030): 229–234 [2019-01-10]. ISSN 1476-4687. doi:10.1038/nature03318. (原始內容存檔於2022-01-21) (英語).
- ^ Umulis, David M.; Serpe, Mihaela; O'Connor, Michael B.; Othmer, Hans G. Robust, bistable patterning of the dorsal surface of the Drosophila embryo. Proceedings of the National Academy of Sciences of the United States of America. 2006-08-01, 103 (31): 11613–11618 [2019-01-10]. ISSN 0027-8424. PMC 1544218
 . PMID 16864795. doi:10.1073/pnas.0510398103. (原始內容存檔於2019-01-10).
. PMID 16864795. doi:10.1073/pnas.0510398103. (原始內容存檔於2019-01-10).
- ^ Graham, Thomas G. W.; Tabei, S. M. Ali; Dinner, Aaron R.; Rebay, Ilaria. Modeling bistable cell-fate choices in the Drosophila eye: qualitative and quantitative perspectives. Development (Cambridge, England). 2010-7, 137 (14): 2265–2278 [2019-01-10]. ISSN 1477-9129. PMC 2889600
 . PMID 20570936. doi:10.1242/dev.044826. (原始內容存檔於2019-01-10).
. PMID 20570936. doi:10.1242/dev.044826. (原始內容存檔於2019-01-10).
- ^ Lai, Karen; Robertson, Matthew J.; Schaffer, David V. The sonic hedgehog signaling system as a bistable genetic switch. Biophysical Journal. 2004-5, 86 (5): 2748–2757 [2019-01-10]. ISSN 0006-3495. PMC 1304145
 . PMID 15111393. doi:10.1016/S0006-3495(04)74328-3. (原始內容存檔於2019-01-10).
. PMID 15111393. doi:10.1016/S0006-3495(04)74328-3. (原始內容存檔於2019-01-10).
- ^ Elf, J.; Ehrenberg, M. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Systems Biology. 2004-12, 1 (2): 230–236 [2019-01-10]. ISSN 1741-2471. PMID 17051695. (原始內容存檔於2019-01-10).
- ^ Kochanczyk, Marek; Jaruszewicz, Joanna; Lipniacki, Tomasz. Stochastic transitions in a bistable reaction system on the membrane. Journal of the Royal Society, Interface. 2013-07-06, 10 (84): 20130151 [2019-01-10]. ISSN 1742-5662. PMC 3673150
 . PMID 23635492. doi:10.1098/rsif.2013.0151. (原始內容存檔於2019-01-10).
. PMID 23635492. doi:10.1098/rsif.2013.0151. (原始內容存檔於2019-01-10).
