在數學裏,線性函數(又稱一次函數)在不同的領域中有多於一個用途和含意。
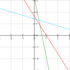
 三個線性函數的圖形都是直線。紅色與藍色直線的斜率相同。紅色與綠色直線的y-截距相同。
三個線性函數的圖形都是直線。紅色與藍色直線的斜率相同。紅色與綠色直線的y-截距相同。
在初等代數與解析幾何,線性函數是只擁有一個變數的一階多項式函數或者是只有常數的函數,因為在直角坐標系中這些函數的圖形是直線。所以,這些函數是線性的。線性函數可以表達為斜截式:
 (
( 為常數且
為常數且 ≠
≠ );
);
其中,  是斜率,
是斜率,  是y-截距,即函數的圖形與y-軸相交的y-坐標。改變斜率
是y-截距,即函數的圖形與y-軸相交的y-坐標。改變斜率  會使直線更陡峭或平緩。改變y-截距
會使直線更陡峭或平緩。改變y-截距  會將直線向上或下平移。
會將直線向上或下平移。
以下三個直線函數的圖形展示於圖右:
 ,
, ,
, 。
。
當 或
或 不同時,一次函數經過的象限也不同,見下表:
不同時,一次函數經過的象限也不同,見下表:
| k的值 |
b的值 |
經過象限 |
圖像
|
 |
 |
第一、二、三象限 |

|
 |
 |
第一、三象限 |

|
 |
 |
第一、三、四象限 |

|
 |
 |
第一、二、四象限 |
|
 |
 |
第二、四象限 |

|
 |
 |
第二、三、四象限 |

|
在高等數學裏的線性代數中,線性函數是一種線性映射,是在兩個向量空間之間,維持向量加法與純量乘法的映射。


例如我們用坐標向量 來表示  與
與  ,那麼線性函數可以表達成
,那麼線性函數可以表達成
 ,當中
,當中 為矩陣。
為矩陣。



























