有限衝激響應 (英語:Finite impulse response ,縮寫FIR)濾波器是其衝激響應 為有限長度的濾波器 ,脈衝輸入信號的響應會在有限時間內變為零,此特性和無限衝激響應 (IIR)濾波器相反,無限衝激響應濾波器存在反饋迴路,其衝激響應 可能是無限長度的(不過一般會衰減)。
N階離散時間的FIR濾波器,其衝激響應 (對應克羅內克δ函數 輸入的輸出)在變為零之前,最多只持續
N
+
1
{\displaystyle N+1}
FIR濾波器可以是連續時間的,也可能是離散時間的,可以是數位 的,也可能是類比 的。
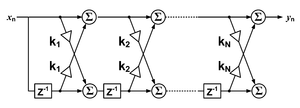
直接型的N階離散FIR濾波器。最上層是N階的延遲線(delay line)和N + 1個抽頭,每一個單元延遲是Z轉換 下的 z −1 運算子 格子型的N階離散FIR濾波器。每一個單元延遲是Z轉換 下的 z −1 運算子 針對因果
y
[
n
]
=
b
0
x
[
n
]
+
b
1
x
[
n
−
1
]
+
⋯
+
b
N
x
[
n
−
N
]
=
∑
i
=
0
N
b
i
⋅
x
[
n
−
i
]
,
{\displaystyle {\begin{aligned}y[n]&=b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{N}x[n-N]\\&=\sum _{i=0}^{N}b_{i}\cdot x[n-i],\end{aligned}}}
其中
x
[
n
]
{\textstyle x[n]}
y
[
n
]
{\textstyle y[n]}
N
{\textstyle N}
N
{\textstyle N}
th 階濾波器表示在右邊有
N
+
1
{\textstyle N+1}
b
i
{\textstyle b_{i}}
N
th
{\textstyle N^{\text{th}}}
0
≤
i
≤
N
{\textstyle 0\leq i\leq N}
b
i
{\textstyle b_{i}}
計算也稱為離散卷積 。
上述項中的
x
[
n
−
i
]
{\textstyle x[n-i]}
tap 數位延遲線
濾波器的衝激響應定義為有限區間內的非零值。包括零值在內,衝激響應是無限數列:
h
[
n
]
=
∑
i
=
0
N
b
i
⋅
δ
[
n
−
i
]
=
{
b
n
0
≤
n
≤
N
0
otherwise
.
{\displaystyle h[n]=\sum _{i=0}^{N}b_{i}\cdot \delta [n-i]={\begin{cases}b_{n}&0\leq n\leq N\\0&{\text{otherwise}}.\end{cases}}}
若FIR濾波器是非因果的,其脈衝響應上的非零值範圍可能從
n
=
0
{\displaystyle n=0}
FIR濾波器相較於IIR濾波器,有以下的優點:
不需要回授,因此捨去誤差不會因為連續的加總而累計。每一次的計算其相對誤差都是一樣的,因此在實現上比較簡單。
在本質上穩定 ,因為其輸出是有限個輸入值乘以有限倍數的和,因此不會大於
∑
|
b
i
|
{\textstyle \sum |b_{i}|}
若讓係數對稱,可以設計成線性相位 地震學 或分音器 )中是很好的特性。 FIR濾波器的主要缺點是若要求要求低頻(相對於取樣率)截止頻率,在相同的銳利程度或是選擇性
數列
x
[
n
]
{\displaystyle x[n]}
卷積定理 ,在頻域上描述:
F
{
x
∗
h
}
⏟
Y
(
ω
)
=
F
{
x
}
⏟
X
(
ω
)
⋅
F
{
h
}
⏟
H
(
ω
)
{\displaystyle \underbrace {{\mathcal {F}}\{x*h\}} _{Y(\omega )}=\underbrace {{\mathcal {F}}\{x\}} _{X(\omega )}\cdot \underbrace {{\mathcal {F}}\{h\}} _{H(\omega )}}
y
[
n
]
=
x
[
n
]
∗
h
[
n
]
=
F
−
1
{
X
(
ω
)
⋅
H
(
ω
)
}
,
{\displaystyle y[n]=x[n]*h[n]={\mathcal {F}}^{-1}{\big \{}X(\omega )\cdot H(\omega ){\big \}},}
其中運算子
F
{\displaystyle {\mathcal {F}}}
F
−
1
{\displaystyle {\mathcal {F}}^{-1}}
H
(
ω
)
{\displaystyle H(\omega )}
頻率響應 ,可以用以下的傅里葉級數 定義:
H
2
π
(
ω
)
≜
∑
n
=
−
∞
∞
h
[
n
]
⋅
(
e
i
ω
)
−
n
=
∑
n
=
0
N
b
n
⋅
(
e
i
ω
)
−
n
,
{\displaystyle H_{2\pi }(\omega )\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot \left({e^{i\omega }}\right)^{-n}=\sum _{n=0}^{N}b_{n}\cdot \left({e^{i\omega }}\right)^{-n},}
其中加上下標表示2π週期性。此處的
ω
{\displaystyle \omega }
正規單位
ω
=
2
π
f
,
{\displaystyle \omega =2\pi f,}
(
f
)
{\displaystyle (f)}
[ A]
f
s
{\displaystyle f_{s}}
samples/second ,
ω
=
2
π
f
/
f
s
{\displaystyle \omega =2\pi f/f_{s}}
(
f
)
{\displaystyle (f)}
cycles/second (赫茲 ),週期性是
f
s
{\displaystyle f_{s}}
ω
=
π
{\displaystyle \omega =\pi }
f
=
f
s
2
{\displaystyle f={\tfrac {f_{s}}{2}}}
Hz
=
1
2
{\displaystyle ={\tfrac {1}{2}}}
cycles/sample 的頻率,也就是奈奎斯特頻率 。
H
2
π
(
ω
)
{\displaystyle H_{2\pi }(\omega )}
離散時間傅里葉變換 表示:
H
^
(
z
)
≜
∑
n
=
−
∞
∞
h
[
n
]
⋅
z
−
n
.
{\displaystyle {\widehat {H}}(z)\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot z^{-n}.}
H
2
π
(
ω
)
=
H
^
(
z
)
|
z
=
e
j
ω
=
H
^
(
e
j
ω
)
.
{\displaystyle H_{2\pi }(\omega )=\left.{\widehat {H}}(z)\,\right|_{z=e^{j\omega }}={\widehat {H}}(e^{j\omega }).}
數位濾波器的設計理念是直接去近似某個離散時間系統的理想頻率響應。在設計有限脈衝響應濾波器時,要找到符合特定規格的係數以及階數,規格可能是時域的(匹配濾波器 ),也可能是頻域的(較常見的情形)。匹配濾波器是將輸入信號和已知形狀的脈波進行互相關(cross-correlation)。FIR摺積(FIR convolution)是脈波響應的逆時間複本(time-reversed copy)和輸入信號進行互相關。因此匹配濾波器的脈波是用針對已知脈波進行取樣,再將取樣信號倒序,做為濾波器的係數[ 1]
若希望有特定的頻率響應,以下是一些常見的濾波器設計方式:
窗函數設計法:理想頻率響應 可由下式表示:
H
d
(
e
j
ω
)
=
∑
n
=
−
∞
∞
h
d
[
n
]
e
−
j
ω
n
{\displaystyle H_{d}(e^{j\omega })=\sum _{n=-\infty }^{\infty }{h_{d}[n]e^{-j\omega n}}}
h
[
n
]
=
h
d
[
n
]
w
[
n
]
{\displaystyle h[n]=h_{d}[n]w[n]}
w
[
n
]
=
{
1
,
0
≤
n
≤
M
,
0
,
otherwise
{\displaystyle w[n]={\begin{cases}1,&0\leq n\leq M{,}\\0,&{\text{otherwise}}\end{cases}}}
H
d
(
e
j
ω
)
{\displaystyle H_{d}(e^{j\omega })}
迴旋積分 。
頻率取樣法:對濾波器的頻率響應 取樣。由下式
H
(
k
)
=
H
d
(
e
j
ω
)
|
ω
=
2
π
N
k
,
k
∈
[
0
,
N
−
1
]
{\displaystyle H(k)=H_{d}(e^{j\omega })|_{\omega ={\frac {2\pi }{N}}k},k\in [0,N-1]}
最小MSE(均方差)法 :定義理想的濾波器頻率響應 ,以及所想要的均方差,將一濾波器的MSE對設計的時脈衝響應偏微分,將偏微分的的式子等於0,用程式最佳化的方式求出數位濾波器的頻率響應。此方法著重在濾波器的頻率響應和理想響應在取樣頻率段的平均誤差。帕克斯-麥克萊倫演算法 :(也稱為是等漣波法、最佳法或Mini-max法)常會用雷米茲演算法 來找最佳等漣波的係數。使用者會標示想要的頻率響應、此響應下誤差的加權函數,以及濾波器階數N。此方法會找到可以將最大偏移量降到最低的
N
+
1
{\textstyle N+1}
N
+
1
{\textstyle N+1}
max
f
|
H
(
f
)
−
H
d
(
f
)
|
{\displaystyle \max _{f}|H(f)-H_{d}(f)|}
[ 2] N ,得到最佳係數的程式。等漣波FIR濾波器也可以用DFT演算法設計[ 3] 目前已有許多軟體可以進行濾波器設計,例如MATLAB 、GNU Octave 、Scilab 和SciPy 等。
簡單FIR濾波器的方塊器(此例中是二階三抽頭的濾波器,是移動平均濾波器)
移動平均 濾波器是簡單的FIR濾波器,有時會稱為Boxcar 函數 濾波器(特別在之後有降採樣 的情形下)。濾波器的係數
b
0
,
…
,
b
N
{\textstyle b_{0},\ldots ,b_{N}}
b
i
=
1
N
+
1
{\displaystyle b_{i}={\frac {1}{N+1}}}
以下是更具體的例子,選擇濾波器的階數:
N
=
2
{\displaystyle N=2}
其沖激響應如下:
h
[
n
]
=
1
3
δ
[
n
]
+
1
3
δ
[
n
−
1
]
+
1
3
δ
[
n
−
2
]
{\displaystyle h[n]={\frac {1}{3}}\delta [n]+{\frac {1}{3}}\delta [n-1]+{\frac {1}{3}}\delta [n-2]}
右邊的方塊圖是以下要討論的二階移動平均濾波器。其遞移函數為:
H
(
z
)
=
1
3
+
1
3
z
−
1
+
1
3
z
−
2
=
1
3
z
2
+
z
+
1
z
2
.
{\displaystyle H(z)={\frac {1}{3}}+{\frac {1}{3}}z^{-1}+{\frac {1}{3}}z^{-2}={\frac {1}{3}}{\frac {z^{2}+z+1}{z^{2}}}.}
下一個圖是濾波器的極零點圖
z
1
=
−
1
2
+
j
3
2
{\textstyle z_{1}=-{\frac {1}{2}}+j{\frac {\sqrt {3}}{2}}}
z
2
=
−
1
2
−
j
3
2
{\textstyle z_{2}=-{\frac {1}{2}}-j{\frac {\sqrt {3}}{2}}}
若以正規化頻率 ω 表示,頻率響應為:
H
(
e
j
ω
)
=
1
3
+
1
3
e
−
j
ω
+
1
3
e
−
j
2
ω
=
1
3
e
−
j
ω
(
1
+
2
c
o
s
(
ω
)
)
.
{\displaystyle {\begin{aligned}H\left(e^{j\omega }\right)&={\frac {1}{3}}+{\frac {1}{3}}e^{-j\omega }+{\frac {1}{3}}e^{-j2\omega }\\&={\frac {1}{3}}e^{-j\omega }\left(1+2cos(\omega )\right).\end{aligned}}}
圖上有其振幅和相位的響應,不過此圖也可以用衝激響應的離散傅里葉變換 得到
因為其對稱性,濾波器設計或是顯示軟體多半只會顯示 [0, π]區域。可以看出移動平均濾波器的低頻增益接近1,但會衰減高頻的信號,因此是簡單的低通濾波器 。相位圖是線性的,但在增益降到零時出現不連續,不連續的大小是π,意思是有變號的情形。最後一張圖的振幅允許正負,此時的相位就都是線性的。
^ Oppenheim, Alan V., Willsky, Alan S., and Young, Ian T.,1983: Signals and Systems, p. 256 (Englewood Cliffs, New Jersey: Prentice-Hall, Inc.) ISBN 0-13-809731-3
^ Rabiner, Lawrence R., and Gold, Bernard, 1975: Theory and Application of Digital Signal Processing (Englewood Cliffs, New Jersey: Prentice-Hall, Inc.) ISBN 0-13-914101-4
^ A. E. Cetin, O.N. Gerek, Y. Yardimci, "Equiripple FIR filter design by the FFT algorithm," IEEE Signal Processing Magazine, pp. 60–64, March 1997.
^ An exception is MATLAB, which prefers units of half-cycles/sample = cycles/2-samples , because the Nyquist frequency in those units is 1, a convenient choice for plotting software that displays the interval from 0 to the Nyquist frequency.



![{\displaystyle {\begin{aligned}y[n]&=b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{N}x[n-N]\\&=\sum _{i=0}^{N}b_{i}\cdot x[n-i],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c43ba6c329a471401e87fe17c6130d801602ffdf)
![{\textstyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298900271d430cdc218444544f75fc47ba51654d)
![{\textstyle y[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0834ff96799c04daf90559cb18c3ef83f9a70de6)





![{\textstyle x[n-i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9faabcad38c6d2a98dfcdfdb635daf0e0366cf54)
![{\displaystyle h[n]=\sum _{i=0}^{N}b_{i}\cdot \delta [n-i]={\begin{cases}b_{n}&0\leq n\leq N\\0&{\text{otherwise}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e64b41f6f07ac049f118cd4e1f80b6a5e7d78d)


![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)

![{\displaystyle y[n]=x[n]*h[n]={\mathcal {F}}^{-1}{\big \{}X(\omega )\cdot H(\omega ){\big \}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aabf8de87f5069e218fed886fa815390345ff5b)



![{\displaystyle H_{2\pi }(\omega )\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot \left({e^{i\omega }}\right)^{-n}=\sum _{n=0}^{N}b_{n}\cdot \left({e^{i\omega }}\right)^{-n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ca9eec5b0a2efb8814181461f1dc7f234784b88)









![{\displaystyle {\widehat {H}}(z)\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot z^{-n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60566e2b445b511e12243d4e01faba9d6ef54cf2)

![{\displaystyle H_{d}(e^{j\omega })=\sum _{n=-\infty }^{\infty }{h_{d}[n]e^{-j\omega n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288ec6efde96f91cc5a2d8423d3d6d6b8eee4803)
![{\displaystyle h[n]=h_{d}[n]w[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ae8fd1bfb873a401b37b8f000b69bb80790f1d6)
![{\displaystyle w[n]={\begin{cases}1,&0\leq n\leq M{,}\\0,&{\text{otherwise}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de33493ffc51183ade60dcf6c340956be353298)

![{\displaystyle H(k)=H_{d}(e^{j\omega })|_{\omega ={\frac {2\pi }{N}}k},k\in [0,N-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12a678f041b4e77c22289fcb5b5d0f08ecd9b749)








![{\displaystyle h[n]={\frac {1}{3}}\delta [n]+{\frac {1}{3}}\delta [n-1]+{\frac {1}{3}}\delta [n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17e21482fe3a56f5731d5e4407d08ff23aee6e2e)



