決策樹學習

決策樹學習是統計學、數據挖掘和機器學習中使用的一種預測建模方法。它使用決策樹作為預測模型（英語：Predictive modelling），從樣本的觀測數據（對應決策樹的分支）推斷出該樣本的預測結果（對應決策樹的葉節點）。

按預測結果的差異，決策樹學習可細分兩類。（1）分類樹，其預測結果僅限於一組離散數值。樹的每個分支對應一組由邏輯與連接的分類特徵，而該分支上的葉節點對應由上述特徵可以預測出的分類標籤。（2）回歸樹，其預測結果為連續值（例如實數）。

在決策分析中，一棵可視的決策樹可以向使用者形象地展示決策的結果和過程。在數據挖掘和機器學習中，一棵決策樹主要用於描述數據（此後亦可基於習得的預測模型去支持決策)。本頁側重描述數據挖掘中的決策樹。

推廣

一個描述泰坦尼克號上乘客生存的決策樹 ("sibsp"指甲板上的兄妹和配偶)。每個決策葉下標識該類乘客的生存幾率和觀察到的比率

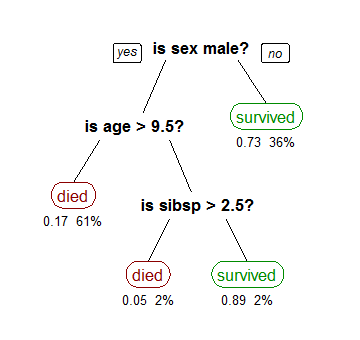
在數據挖掘中決策樹訓練是一個常用的方法。目標是創建一個模型來預測樣本的目標值。例如右圖。每個內部節點對應於一個輸入屬性，子節點代表父節點的屬性的可能取值。每個葉子節點代表輸入屬性得到的可能輸出值。

一棵樹的訓練過程為：根據一個指標，分裂訓練集為幾個子集。這個過程不斷的在產生的子集裡重複遞歸進行，即遞歸分割。當一個訓練子集的類標都相同時遞歸停止。這種「決策樹的自頂向下歸納」（TDITD）^[1]是貪心算法的一種, 也是目前為止最為常用的一種訓練方法，但不是唯一的方法。

數據以如下方式表示:

({\textbf {x}},Y)=(x_{1},x_{2},x_{3},...,x_{k},Y)

其中Y是目標值，向量x由這些屬性構成, x₁, x₂, x₃ 等等，用來得到目標值。

決策樹的類型

在數據挖掘中，決策樹主要有兩種類型:

分類樹 的輸出是樣本的類標（例如花的分類，股票漲跌等）。
回歸樹 的輸出是一個實數 (例如房子的價格，病人待在醫院的時間等)。

術語分類和回歸樹 (CART) 包含了上述兩種決策樹, 最先由Breiman 等提出.^[2] 分類樹和回歸樹有些共同點和不同點—例如處理在何處分裂的問題。^[2]

有些集成的方法產生多棵樹：

裝袋算法（Bagging）, 是一個早期的集成方法，用有放回抽樣法來訓練多棵決策樹，最終結果用投票法產生。^[3]
隨機森林（Random Forest） 使用多棵決策樹來改進分類性能。
提升樹（Boosting Tree） 可以用來做回歸分析和分類決策^[4]^[5]
旋轉森林（Rotation forest） – 每棵樹的訓練首先使用主元分析法 (PCA)。^[6]

還有其他很多決策樹算法，常見的有:

ID3算法
C4.5算法
CHi-squared Automatic Interaction Detector (CHAID). 在生成樹的過程中用多層分裂.^[7]
MARS:可以更好的處理數值型數據。

模型表達式

構建決策樹時通常採用自上而下的方法，在每一步選擇一個最好的屬性來分裂。^[8] "最好" 的定義是使得子節點中的訓練集儘量的純，表示所分裂出的子節點中的集合越相近。不同的算法使用不同的指標來定義"最好"。本部分介紹一些最常見的指標。

基尼不純度指標

在CART算法中, 基尼不純度表示一個隨機選中的樣本在子集中被分錯的可能性。基尼不純度為這個樣本被選中的概率乘以它被分錯的概率。當一個節點中所有樣本都是一個類時，基尼不純度為零。

假設y的可能取值為 $J$ 個類別，令 $i\in \{1,2,...,J\}$ ， $p_{i}$ 表示被標定為第 $i$ 類的概率，則基尼不純度的計算為：

\operatorname {I} _{G}(p)=\sum _{i=1}^{J}p_{i}\sum _{k\neq i}p_{k}=\sum _{i=1}^{J}p_{i}(1-p_{i})=\sum _{i=1}^{J}(p_{i}-{p_{i}}^{2})=\sum _{i=1}^{J}p_{i}-\sum _{i=1}^{J}{p_{i}}^{2}=1-\sum _{i=1}^{J}{p_{i}}^{2}

信息增益

ID3, C4.5 和 C5.0 決策樹的生成使用信息增益。信息增益是基於信息論中信息熵與資訊本體理論。

信息熵定義為：

\mathrm {H} (T)=\operatorname {I} _{E}\left(p_{1},p_{2},...,p_{J}\right)=-\sum _{i=1}^{J}{p_{i}\log _{2}p_{i}}

其中 $p_{1},p_{2},...$ 加和為1，表示當前節點中各個類別的百分比。^[9]

\overbrace {IG(T,a)} ^{\text{Information Gain}}=\overbrace {\mathrm {H} (T)} ^{\text{Entropy (parent)}}-\overbrace {\mathrm {H} (T|a)} ^{\text{Weighted Sum of Entropy (Children)}}

=-\sum _{i=1}^{J}p_{i}\log _{2}{p_{i}}-\sum _{a}{p(a)\sum _{i=1}^{J}-\Pr(i|a)\log _{2}{\Pr(i|a)}}

例如，數據集有4個屬性：outlook (sunny, overcast, rainy), temperature (hot, mild, cool), humidity (high, normal), and windy (true, false), 目標值play（yes, no）, 總共14個數據點。為建造決策樹，需要比較4棵決策樹的信息增益，每棵決策樹用一種屬性做劃分。信息增益最高的劃分作為第一次劃分，並在每個子節點繼續此過程，直至其信息增益為0。

使用屬性windy做劃分時，產生2個子節點：windy值為真與為假。當前數據集，6個數據點的windy值為真，其中3個點的play值為真，3個點的play值為假；其餘8個數據點的windy為假，其中6個點的play值為真，2個點的play值為假。 windy=true的子節點的信息熵計算為：

I_{E}([3,3])=-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}=-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}=1

windy=false的子節點的信息熵計算為：

I_{E}([6,2])=-{\frac {6}{8}}\log _{2}^{}{\frac {6}{8}}-{\frac {2}{8}}\log _{2}^{}{\frac {2}{8}}=-{\frac {3}{4}}\log _{2}^{}{\frac {3}{4}}-{\frac {1}{4}}\log _{2}^{}{\frac {1}{4}}=0.8112781

這個劃分（使用屬性windy）的信息熵是兩個子節點信息熵的加權和：

I_{E}([3,3],[6,2])=I_{E}({\text{windy or not}})={\frac {6}{14}}\cdot 1+{\frac {8}{14}}\cdot 0.8112781=0.8921589

為計算使用屬性windy的信息增益，必須先計算出最初（未劃分）的數據集的信息熵，數據集的play有9個yes與5個no：

I_{E}([9,5])=-{\frac {9}{14}}\log _{2}^{}{\frac {9}{14}}-{\frac {5}{14}}\log _{2}{\frac {5}{14}}=0.940286

使用屬性windy的信息增益是：

IG({\text{windy}})=I_{E}([9,5])-I_{E}([3,3],[6,2])=0.940286-0.8921589=0.0481271

決策樹的優點

與其他的數據挖掘算法相比，決策樹有許多優點:

易於理解和解釋，人們很容易理解決策樹的意義。
只需很少的數據準備，其他技術往往需要數據歸一化。
即可以處理數值型數據也可以處理類別變數數據。其他技術往往只能處理一種數據類型。例如關聯規則只能處理類別型的而神經網絡只能處理數值型的數據。
使用白箱模型，輸出結果容易通過模型的結構來解釋。而神經網絡是黑箱模型，很難解釋輸出的結果。
可以通過測試集來驗證模型的性能。可以考慮模型的穩定性。
強健控制。對噪聲處理有好的強健性。
可以很好的處理大規模數據。

缺點

訓練一棵最優的決策樹是一個完全NP問題。^[10]^[11] 因此, 實際應用時決策樹的訓練採用啟發式搜索算法例如貪心算法來達到局部最優。這樣的算法沒辦法得到最優的決策樹。
決策樹創建的過度複雜會導致無法很好的預測訓練集之外的數據。這稱作過擬合.^[12] 剪枝機制可以避免這種問題。
有些問題決策樹沒辦法很好的解決,例如異或問題。解決這種問題的時候，決策樹會變得過大。要解決這種問題，只能改變問題的領域^[13] 或者使用其他更為耗時的學習算法(例如統計關係學習（英語：Statistical relational learning）或者歸納邏輯程式設計（英語：Inductive logic programming）).

對那些有類別型屬性的數據，信息增益會有一定的偏置。^[14]

延伸

決策圖

在決策樹中, 從根節點到葉節點的路徑採用匯合。而在決策圖中, 可以採用最小描述長度（MML）來匯合兩條或多條路徑。^[15]

用演化算法來搜索

演化算法可以用來避免局部最優的問題^[16]^[17]

參見

參考資料

^ Quinlan, J. R., (1986). Induction of Decision Trees. Machine Learning 1: 81-106, Kluwer Academic Publishers
^ ^2.0 ^2.1 Breiman, Leo; Friedman, J. H., Olshen, R. A., & Stone, C. J. Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. 1984. ISBN 978-0-412-04841-8.
^ Breiman, L. (1996). Bagging Predictors. "Machine Learning, 24": pp. 123-140.
^ Friedman, J. H. (1999). Stochastic gradient boosting. Stanford University.
^ Hastie, T., Tibshirani, R., Friedman, J. H. (2001). The elements of statistical learning : Data mining, inference, and prediction. New York: Springer Verlag.
^ Rodriguez, J.J. and Kuncheva, L.I. and Alonso, C.J. (2006), Rotation forest: A new classifier ensemble method, IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(10):1619-1630.
^ Kass, G. V. An exploratory technique for investigating large quantities of categorical data. Applied Statistics. 1980, 29 (2): 119–127. JSTOR 2986296. doi:10.2307/2986296.
^ Rokach, L.; Maimon, O. Top-down induction of decision trees classifiers-a survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C. 2005, 35 (4): 476–487. doi:10.1109/TSMCC.2004.843247.
^ Witten, Ian; Frank, Eibe; Hall, Mark. Data Mining. Burlington, MA: Morgan Kaufmann. 2011: 102–103. ISBN 978-0-12-374856-0.
^ Hyafil, Laurent; Rivest, RL. Constructing Optimal Binary Decision Trees is NP-complete. Information Processing Letters. 1976, 5 (1): 15–17. doi:10.1016/0020-0190(76)90095-8.
^ Murthy S. (1998). Automatic construction of decision trees from data: A multidisciplinary survey. Data Mining and Knowledge Discovery
^ Principles of Data Mining. SpringerLink. [2018-04-02]. doi:10.1007/978-1-84628-766-4 （英國英語）.
^ Inductive Logic Programming. SpringerLink. [2018-04-02]. doi:10.1007/b13700 （英國英語）.
^ Deng,H.; Runger, G.; Tuv, E. Bias of importance measures for multi-valued attributes and solutions (PDF). Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN): 293–300. 2011 [2018-05-10]. （原始內容 (PDF)存檔於2018-05-10）.
^ 存档副本. [2012-05-26]. （原始內容存檔於2008-03-21）.
^ Papagelis A., Kalles D.(2001). Breeding Decision Trees Using Evolutionary Techniques, Proceedings of the Eighteenth International Conference on Machine Learning, p.393-400, June 28-July 01, 2001
^ Barros, Rodrigo C., Basgalupp, M. P., Carvalho, A. C. P. L. F., Freitas, Alex A. (2011). A Survey of Evolutionary Algorithms for Decision-Tree Induction. IEEE Transactions on Systems, Man and Cybernetics, Part C: Applications and Reviews, vol. 42, n. 3, p. 291-312, May 2012.

外部連結

Building Decision Trees in Python From O'Reilly.
An Addendum to "Building Decision Trees in Python"（頁面存檔備份，存於網際網路檔案館） From O'Reilly.
Decision Trees page at aaai.org, a page with commented links.
Decision tree implementation in Ruby (AI4R)（頁面存檔備份，存於網際網路檔案館）
Building Decision Tree In Bash（頁面存檔備份，存於網際網路檔案館）

[Quinlan86-1] Quinlan, J. R., (1986). Induction of Decision Trees. Machine Learning 1: 81-106, Kluwer Academic Publishers

[bfos-2] 2.0 ^2.1 Breiman, Leo; Friedman, J. H., Olshen, R. A., & Stone, C. J. Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. 1984. ISBN 978-0-412-04841-8.

[3] Breiman, L. (1996). Bagging Predictors. "Machine Learning, 24": pp. 123-140.

[4] Friedman, J. H. (1999). Stochastic gradient boosting. Stanford University.

[5] Hastie, T., Tibshirani, R., Friedman, J. H. (2001). The elements of statistical learning : Data mining, inference, and prediction. New York: Springer Verlag.

[6] Rodriguez, J.J. and Kuncheva, L.I. and Alonso, C.J. (2006), Rotation forest: A new classifier ensemble method, IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(10):1619-1630.

[7] Kass, G. V. An exploratory technique for investigating large quantities of categorical data. Applied Statistics. 1980, 29 (2): 119–127. JSTOR 2986296. doi:10.2307/2986296.

[8] Rokach, L.; Maimon, O. Top-down induction of decision trees classifiers-a survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C. 2005, 35 (4): 476–487. doi:10.1109/TSMCC.2004.843247.

[Witten_2011_102–103-9] Witten, Ian; Frank, Eibe; Hall, Mark. Data Mining. Burlington, MA: Morgan Kaufmann. 2011: 102–103. ISBN 978-0-12-374856-0.

[10] Hyafil, Laurent; Rivest, RL. Constructing Optimal Binary Decision Trees is NP-complete. Information Processing Letters. 1976, 5 (1): 15–17. doi:10.1016/0020-0190(76)90095-8.

[11] Murthy S. (1998). Automatic construction of decision trees from data: A multidisciplinary survey. Data Mining and Knowledge Discovery

[12] Principles of Data Mining. SpringerLink. [2018-04-02]. doi:10.1007/978-1-84628-766-4 （英國英語）.

[13] Inductive Logic Programming. SpringerLink. [2018-04-02]. doi:10.1007/b13700 （英國英語）.

[14] Deng,H.; Runger, G.; Tuv, E. Bias of importance measures for multi-valued attributes and solutions (PDF). Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN): 293–300. 2011 [2018-05-10]. （原始內容 (PDF)存檔於2018-05-10）.

[15] 存档副本. [2012-05-26]. （原始內容存檔於2008-03-21）.

[16] Papagelis A., Kalles D.(2001). Breeding Decision Trees Using Evolutionary Techniques, Proceedings of the Eighteenth International Conference on Machine Learning, p.393-400, June 28-July 01, 2001

[17] Barros, Rodrigo C., Basgalupp, M. P., Carvalho, A. C. P. L. F., Freitas, Alex A. (2011). A Survey of Evolutionary Algorithms for Decision-Tree Induction. IEEE Transactions on Systems, Man and Cybernetics, Part C: Applications and Reviews, vol. 42, n. 3, p. 291-312, May 2012.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]