齐次蒙日-安培方程(Homogeneous Monge-Ampère equation)是一个常见于黎曼几何的非线性偏微分方程,同时也是卡拉比-丘流形证明时曾用的工具。[1]
广义而言,定义两个独立变量x,y,以及一个非独立变量u,蒙日-安培方程可以表述为:
![{\displaystyle L[u]=A(u_{xx}u_{yy}-u_{xy}^{2})+Bu_{xx}+2Cu_{xy}+Du_{yy}+E=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dddc4aaf071d2a12695ffabc119672ed8b3e98f6)
这里的A,B,C,D,E为一阶变量x,y,ux和uy唯一的非独立函数。
根据齐次蒙日-安培方程:
![{\displaystyle sys={(U[x,t])^{2}-U[x,x]*U[t,t]=0};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20a29466ff9b71ca6c07055a705ef349c4e7d4a4)
其对应的解析解为:
![{\displaystyle u[1]:=C1*y^{2}+C2*x*y+C2^{2}*x^{2}/(4*C1)+C3*y+C4*x+C5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60d4c580b93b6c33c4d6132c80b4f247e21c2eeb)
![{\displaystyle u[2]:=(C2*y^{2}+C3*y+C3^{2}/(4*C2))/(x+C1)+C4*y+C5*x+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e79ef20f1d20364e35b7b99f6b5058603462dc4)
![{\displaystyle u[3]:=(C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e1b5c8b3ab69b0009d6a2f387fb3e22b0ebcad)
![{\displaystyle u[4]:=(C1*x+C2*y+C3)^{k}+C4*x+C5*y+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/334732a28c4d6a164e53acd92d7036fce756ec8c)
![{\displaystyle u[5]:=-(C1*x+C2*y+C3)^{k}+C4*x+C5*y+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c6b32c035f8fc7b4d3a48a4b5041c460374d03)
![{\displaystyle u[6]:=-(C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48ff45ede72b9f92155b81b610cff26aeae3ca02)
![{\displaystyle u[7]:={\sqrt {C1*x^{2}+2*C1*x*a+C1*a^{2}+C2*x*y+C2*x*b+C2*a*y+C2*a*b+C3*y^{2}+2*C3*y*b+C3*b^{2}}}+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/519771b2bf015373532dd18caf208fff1e49267e)
![{\displaystyle u[8]:=C1*(C1*y^{2}+C2*x*y+(1/4)*C2^{2}*x^{2}/C1+C3*y+C4*x+C5)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bffb672374e71152d07dcdff0b24c9930650442c)
![{\displaystyle u[9]:=C1*((C2*y^{2}+C3*y+(1/4)*C3^{2}/C2)/(x+C1)+C4*y+C5*x+C6)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e403dbda155fa7e8589bb09a8e0da8631ef93b2a)
![{\displaystyle u[10]:=C1*((C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb6e527ddab97b5c7b7f28f4cafe38dd37ca14c)
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
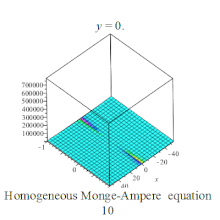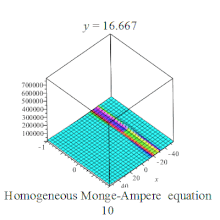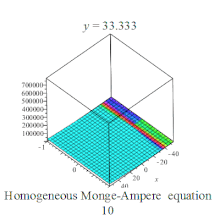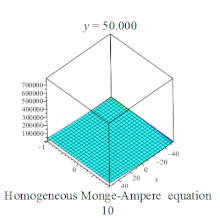 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
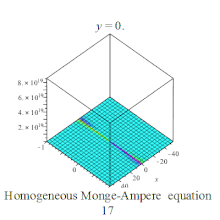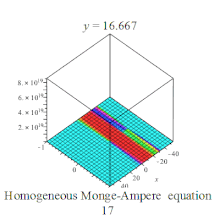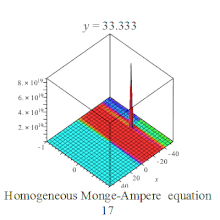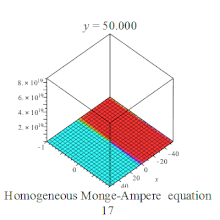 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
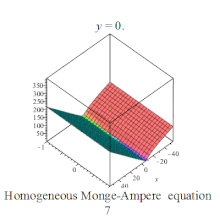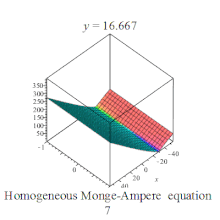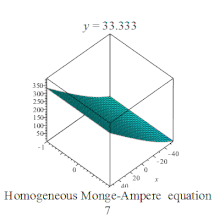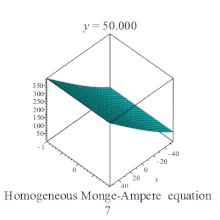 Homogeneous Monge-Ampere equation plot Homogeneous Monge-Ampere equation plot
|
- ^ Andrei D. Polyanin,Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION p775-776 CRC PRESS
- *谷超豪 《孤立子理论中的达布变换及其几何应用》 上海科学技术出版社
- *阎振亚著 《复杂非线性波的构造性理论及其应用》 科学出版社 2007年
- 李志斌编著 《非线性数学物理方程的行波解》 科学出版社
- 王东明著 《消去法及其应用》 科学出版社 2002
- *何青 王丽芬编著 《Maple 教程》 科学出版社 2010 ISBN 9787030177445
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759













![{\displaystyle L[u]=A(u_{xx}u_{yy}-u_{xy}^{2})+Bu_{xx}+2Cu_{xy}+Du_{yy}+E=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dddc4aaf071d2a12695ffabc119672ed8b3e98f6)
![{\displaystyle sys={(U[x,t])^{2}-U[x,x]*U[t,t]=0};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20a29466ff9b71ca6c07055a705ef349c4e7d4a4)
![{\displaystyle u[1]:=C1*y^{2}+C2*x*y+C2^{2}*x^{2}/(4*C1)+C3*y+C4*x+C5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60d4c580b93b6c33c4d6132c80b4f247e21c2eeb)
![{\displaystyle u[2]:=(C2*y^{2}+C3*y+C3^{2}/(4*C2))/(x+C1)+C4*y+C5*x+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e79ef20f1d20364e35b7b99f6b5058603462dc4)
![{\displaystyle u[3]:=(C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e1b5c8b3ab69b0009d6a2f387fb3e22b0ebcad)
![{\displaystyle u[4]:=(C1*x+C2*y+C3)^{k}+C4*x+C5*y+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/334732a28c4d6a164e53acd92d7036fce756ec8c)
![{\displaystyle u[5]:=-(C1*x+C2*y+C3)^{k}+C4*x+C5*y+C6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c6b32c035f8fc7b4d3a48a4b5041c460374d03)
![{\displaystyle u[6]:=-(C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48ff45ede72b9f92155b81b610cff26aeae3ca02)
![{\displaystyle u[7]:={\sqrt {C1*x^{2}+2*C1*x*a+C1*a^{2}+C2*x*y+C2*x*b+C2*a*y+C2*a*b+C3*y^{2}+2*C3*y*b+C3*b^{2}}}+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/519771b2bf015373532dd18caf208fff1e49267e)
![{\displaystyle u[8]:=C1*(C1*y^{2}+C2*x*y+(1/4)*C2^{2}*x^{2}/C1+C3*y+C4*x+C5)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bffb672374e71152d07dcdff0b24c9930650442c)
![{\displaystyle u[9]:=C1*((C2*y^{2}+C3*y+(1/4)*C3^{2}/C2)/(x+C1)+C4*y+C5*x+C6)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e403dbda155fa7e8589bb09a8e0da8631ef93b2a)
![{\displaystyle u[10]:=C1*((C1*x+C2*y+C3)^{(}k+1)/(C4*x+C5*y+C6)^{k}+C7*x+C8*y+C9)*(C2*x+C3*y+C4)+C5*x+C6*y+C7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb6e527ddab97b5c7b7f28f4cafe38dd37ca14c)