隐藏吸引子
隐藏吸引子(hidden attractor)是动力系统中一种特别的吸引子,系统中不但有稳定的振荡(极限环或混沌吸引子),也存在唯一的稳定平衡点。
在动力系统的分岔理论中,若有不失去平稳集稳定性的有界振荡,会称为是隐藏振荡(hidden oscillation)。在非线性控制理论中,非时变系统出现状态有界的隐藏振荡,表示其越过了参数域的边界,平稳集的局部稳定性也表示全域的稳定性(卡尔曼猜想)。若隐藏振荡(或是动力系统相空间内的某隐藏振荡子集)可以吸引邻近几乎所有的振荡,则称为是隐藏吸引子(hidden attractor)。
针对有单一平衡点,而且平衡点具有全域吸引性的动力系统,隐藏振荡的出现表示其行为特性的改变,由单稳定性变成双稳定性(bi-stability)。一般来说,动力系统会变成多稳态,同时在相空间中会同时出现局部的吸引子。平凡吸引子(稳定的平衡点)可以用解析或是数值的方式求得。但要找极限环(周期吸引子)或混沌吸引子的困难度就很高了(参考希尔伯特第十六问题)。
将吸引子分为隐藏或自激两类
[编辑]为了要识别物理系统或是数值实验中的局部吸引子,需要在吸引子的吸引区域(basin of attraction)中选定一点为初始状态,观察系统状态从初始状态开始后,吸引子的特性。将吸引子分为隐藏或自激两类,本身就反映出在相空间中找局部吸引子吸引区域的困难点。
定义[1][2][3] 若吸引子的吸引区域没有和其他平衡点的开放邻域有交集,此吸引子称为隐藏吸引子(hidden attractor),否则,此吸引子称为自激吸引子(self-excited attractor)。
将吸引子分为隐藏或自激的想法是由Gennady Leonov和Nikolay V. Kuznetsov提出的,和2009年首次发现蔡氏电路中的隐藏吸引子有关[4][5][6][7]。同样的,任何有界的振荡,若在相空间中不一定有开邻界的吸引区域,则可以分类为自激振荡或隐藏振荡。

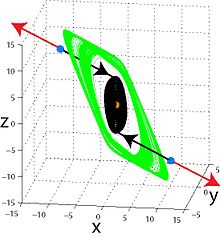

自激吸引子
[编辑]针对自激吸引子,其吸引区域会伴随一个不稳定的平衡点,因此可以用标准数值的程序来找自激吸引子,使轨迹从不稳定平衡点的邻域开始,看是否会被吸引到某个振荡状态中,若有,即为自激吸引子(自激振荡)。因此,自激吸引子就算和多稳态一起出现,也可用数值的方式发现吸引子,并加以视觉化。在洛伦茨吸引子中,针对经典的参数下,吸引子相对所有存在的平衡点都是自激吸引子, 可以在其附近将轨迹视觉化。不过有些参数下,会有二个平凡的吸引子和自激的混沌吸引子并存(自激吸引子只和不稳定的零平衡点有关)。Van der Pol、B-Z反应、若斯叻吸引子、蔡氏电路和厄农映射的吸引子都是自激吸引子。
伊甸猜想是猜想自激吸引子的李雅普诺夫维数,不会超过对应不稳定流形的李雅普诺夫维数,也就是和吸引子吸引区域有重叠的不稳定流形[8]。
隐藏吸引子
[编辑]隐藏吸引子也有吸引区域,但不和其他的平衡点相连,因此在相空间中是“隐藏”的。例如,隐藏吸引子可能是以下系统的吸引子:没有平衡点的系统(例如1902年提出,有Sommerfeld效应的旋转机电系统)、只有一个平衡点,且稳定的系统(例如阿依热尔曼猜想的反例以及卡尔曼猜想的反例,这些猜想都是有关非线性控制系统的单稳定性)。最早提出的相关理论问题是希尔伯特第十六问题的后半部,此问题是有关二维多项式系统中,极限环的数量以及相互的位置,而嵌套的稳定极限环就是隐藏的周期吸引子。隐藏吸引子的概念已成为许多应用的动态模型中,发现隐藏吸引子的催化剂[1][9][10]。
一般而言,有关隐藏吸引子的问题,没有通用直接的方式来追踪或是预测系统是否会有隐藏吸引子(例如[11])。不过针对二维系统,可以用解析方式观测隐藏吸引子(例如希尔伯特第十六问题的第二个问题)。若要研究复杂非线性多维系统的稳定性和振荡,多半会用数值方法进行。 在多维系统中,不太可能用乱数初始资料进行轨迹积分来找区域性的隐藏吸引子,原因是其吸引区域可能很小,而且其维度可能比系统的维度要小很多。因此这种问题的数值区域化需要发展特殊的数值解析计算程序[1][12][8],可以选择隐藏吸引子吸引区域中的一点作为启始点(不包括平衡点的邻域),再进行轨迹计算。也有一些以同伦(homotopy)和数值延拓法(numerical continuation)为基础的有效方式:是建构类似系统的程序,此程序使得针对第一个系统(启始系统)要数值计算振荡解(启始振荡)的初值可以用解析方式求得,接下来将启始振荡转换到允许数值计算的第二个系统。
隐藏吸引子理论
[编辑]将吸引子分为自激吸引子和隐藏吸引子,是出现隐藏振荡理论的基本前提,这代表了安德罗诺夫(Andronov)隐藏理论的现代发展。找到全域稳定性的确切边界是关键。N. Kuznetsov将全域稳定性分类为平凡的(依局部的分叉决定)或隐藏的(依照非局部的分叉以及隐藏振荡的出现)两类[13][14]。
参考资料
[编辑]- ^ 1.0 1.1 1.2 Leonov G.A.; Kuznetsov N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. 2013, 23 (1): 1330002–219. Bibcode:2013IJBC...2330002L. doi:10.1142/S0218127413300024
 .
.
- ^ Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits (PDF). Journal of Computer and Systems Sciences International. 2011, 50 (5): 511–543 [2021-06-29]. S2CID 21657305. doi:10.1134/S106423071104006X. (原始内容存档 (PDF)于2016-03-04).
- ^ Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. The European Physical Journal Special Topics. 2015, 224 (8): 1421–1458. S2CID 119227870. arXiv:1505.04729
 . doi:10.1140/epjst/e2015-02470-3.
. doi:10.1140/epjst/e2015-02470-3.
- ^ Kuznetsov N.V.; Leonov G.A.; Vagaitsev V.I. Analytical-numerical method for attractor localization of generalized Chua's system. IFAC Proceedings Volumes. 2010, 43 (11): 29–33. doi:10.3182/20100826-3-TR-4016.00009.
- ^ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. Localization of hidden Chua's attractors (PDF). Physics Letters. 2011, 375 (23): 2230–2233 [2021-06-29]. Bibcode:2011PhLA..375.2230L. doi:10.1016/j.physleta.2011.04.037. (原始内容存档 (PDF)于2022-01-19).
- ^ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. Hidden attractor in smooth Chua systems (PDF). Physica D. 2012, 241 (18): 1482–1486 [2021-06-29]. Bibcode:2012PhyD..241.1482L. doi:10.1016/j.physd.2012.05.016. (原始内容存档 (PDF)于2022-01-19).
- ^ 8.0 8.1 Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N.; Prasad, A.; Shrimali, M.D. Finite-time Lyapunov dimension and hidden attractor of the Rabinovich system. Nonlinear Dynamics. 2018, 92 (2): 267–285. S2CID 54706479. arXiv:1504.04723
 . doi:10.1007/s11071-018-4054-z.
. doi:10.1007/s11071-018-4054-z.
- ^ Kuznetsov N. V.; Leonov G. A. Hidden attractors in dynamical systems: systems with no equilibria, multistability and coexisting attractors. IFAC Proceedings Volumes (IFAC World Congress Proceedings). 2014, 47 (3): 5445–5454. doi:10.3182/20140824-6-ZA-1003.02501.
- ^ Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. Hidden attractors in dynamical models of phase-locked loop circuits: limitations of simulation in MATLAB and SPICE. Communications in Nonlinear Science and Numerical Simulation. 2017, 51: 39–49. Bibcode:2017CNSNS..51...39K. doi:10.1016/j.cnsns.2017.03.010.
- ^ Chen, G.; Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N. Hidden attractors on one path: Glukhovsky-Dolzhansky, Lorenz, and Rabinovich systems. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. 2015, 27 (8): art. num. 1750115. S2CID 21425647. arXiv:1705.06183
 . doi:10.1142/S0218127417501152.
. doi:10.1142/S0218127417501152.
- ^ Kuznetsov N.V. Theory of hidden oscillations and stability of control systems (PDF). Journal of Computer and Systems Sciences International. 2020, 59 (5): 647–668. doi:10.1134/S1064230720050093.
- ^ Kuznetsov, N.V.; Mokaev, T.N.; Kuznetsova, O.A.; Kudryashova, E.V. The Lorenz system: hidden boundary of practical stability and the Lyapunov dimension. Nonlinear Dynamics. 2020, 102 (2): 713–732 [2021-06-28]. doi:10.1007/s11071-020-05856-4
 . (原始内容存档于2021-06-28).
. (原始内容存档于2021-06-28).
书籍
[编辑]- Chaotic Systems with Multistability and Hidden Attractors (Eds.: Wang, Kuznetsov, Chen), Springer, 2021 (doi:10.1007/978-3-030-75821-9 (页面存档备份,存于互联网档案馆))
- Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors (Eds.: Pham, Vaidyanathan, Volos et al.), Springer, 2018 (doi:10.1007/978-3-319-71243-7)
