连续函数 (拓扑学)
外观
(重定向自连续映射 (拓扑学))
此条目没有列出任何参考或来源。 (2015年9月23日) |
在拓扑学和数学的相关领域里,连续函数是指在拓扑空间之间的一种态射。直观上来说,其为一个函数f,其中每一群在f(x)附近的点都会含有在x附近的一群点之值。对一个一般的拓扑空间来说,这是指f(x)的邻域总会包含着x之邻域的值。
在一个度量空间(如实数)里,这是指在f(x)一定距离内的点总会包含着在x某些距离内的所有点。
定义
[编辑]因为有若干个对拓扑结构的等价定义存在,所以亦存在若干种定义连续函数的方法。
开集与闭集定义
[编辑]拓扑中最常见的连续概念之定义为将其定义为一个其开集之前像亦为开集的函数。类似开集的公式化,亦有一闭集公式化,其将连续函数定义为其闭集之前像亦为闭集的函数。
邻域定义
[编辑]以前像为基底之定义时常很难直接地被使用。替代地,设有一由X至Y的函数f,其中的X和Y都是拓扑空间。则f会被称为是在x为连续的,其中x为X的元素,若对于任一f(x)的邻域V,都存在一个能使之x的邻域U。虽然此一定义看起来很复杂,其在直觉上是指不论V变得多“小”,总会可以找到一个包含可映射至V内之x的U。若f在X内的每一个元素x都会连续,则简称f是连续的。
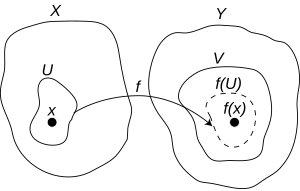
在一度量空间内,则其会等价于将所有邻域替换成考量以x和f(x)为中心之开球的邻域系统。这会导致在实分析中对连续函数的标准定义,其叙述著一个函数若为连续时,则其靠近x的所有点都会映射至靠近f(x)的点上。这只在度量空间中有意义,因为只有在度量空间中有距离的概念。
数列和网
[编辑]在一些文章中,空间的拓扑会被简便地以极限点来描述。

