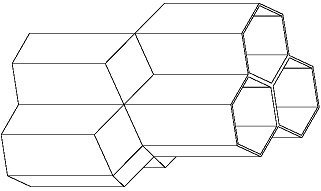
蜂房
此条目介绍的是蜜蜂巢穴里六角形的构造。关于蜜蜂巢穴本身，请见“蜂巢”。
蜂房或者蜂窝是蜜蜂所建巢穴里的构造，由众多正六边形的蜂蜡巢室所组成。蜂房里除了蜜蜂之外，还有它们的幼虫，并储存蜂蜜和花粉。而马蜂亚科（Polistinae）和胡蜂亚科（Vespinae）的胡蜂所建立的蜂巢则是用纸所造成的，而非蜂蜡。
养蜂家会拆掉整个蜂巢去获取蜂蜜。蜂蜜的提取可以透过打开蜂箱取出巢框，然后把它放进分离蜂蜜的离心机里旋转。另外，有时候新的蜜脾会以不加工的巢蜜形式售卖。
孵化养育蜜蜂幼虫的蜂房经过一段时间后，会渐渐变黑，因为茧会嵌进巢室，养蜂家称为“活动污迹”（Travel Stain）。“蜜继箱”（Honey Super）上的巢脾因为没有用来孵化养育蜜蜂幼虫，所以便会保持光亮颜色。
蜂房的几何形状
[编辑]蜂房的中心线总是似是水平的，而巢室的非角度行排（non-angled rows）也是水平地（非垂直地）排成一线。因此，每个巢室都有两个垂直的“墙”，由两个角墙构成“地板”和“天花板”。而巢室的斜度是些微地向上，在9至14度之间，朝向开端，这样蜂蜜便不至流出。
那么为什么蜂房是六边形，而非其他形状的？现在的说法有两个。第一种说法由波兰数学家、物理学家暨天文学家Jan Brożek提出，六边形能以每范围最小的周界去平铺一平面，就是说六边形结构可以在一定体积里，能用最少的材料去建造一个最宽敞的巢室。另一种说法由苏格兰生物学家、数学家暨古典学者达西·汤普森（D'Arcy Wentworth Thompson）提出，他认为六边形形状是基于个别的蜜蜂们将巢室摆放在一起的程序：有些类似在肥皂泡间制造的边界形状。为支持此论点，他指出个别建造的蜂王巢室，它们多是不规则和凹凸不平，不是以最有效率的方式制作。
蜜蜂建筑蜂巢似乎是基于它们的本能，生物学一般的理论均认为自然界里这么有效能的形状的现象是由于自然选择。
蜂房巢室的末端也是几何效能的例子，虽然是三维和不起眼。末端是一个所有邻近表面两面角度为120°的三面锥形，在一定容量最小化表面面积的角度（一个在锥形顶部边缘形成的角度大约为109°28'16"（ = 180°- arccos（1/3）））。
蜂巢巢室3D几何图。
巢室的形状就像是两个相对的蜂巢层互相套叠对方，而末端的各个平面都是和对边的巢室共用的。
相对层蜂巢的巢室合并在一起。
当然个别巢室并非如上图显示的几何完美：在一个实际的蜂房里，"完美"的六边形是有少许百分比偏差的。在较大的雄蜂蜂巢和较小的工蜂蜂巢之间的过渡地区，或当蜜蜂遇到障碍时，巢室型状都可能会歪曲的。而在1965年，匈牙利数学家拉兹洛·费耶·托斯发现蜜蜂所用的三面锥形（由三个菱形组成）不是理想最佳的三维几何形状。而由2个六角形和2个较小菱形组成的巢室末端将会多.035%（或接近1/2850）的效能。
参见
[编辑]参考书目
[编辑]- Graham, Joe. The Hive and the Honey Bee. Hamilton/IL: Dadant & Sons; 1992; ISBN 0-915698-09-9
- Thompson, D'Arcy Wentworth (1942). On Growth and Form. Dover Publications. ISBN 0-486-67135-6.
- "The Mathematics of the Honeycomb" (June 1985). Science Digest, pp. 74-77.
外部链接
[编辑]
- 最杰出的建筑师──蜜蜂 （页面存档备份，存于互联网档案馆）（繁体中文）