 双头欧拉螺线
双头欧拉螺线
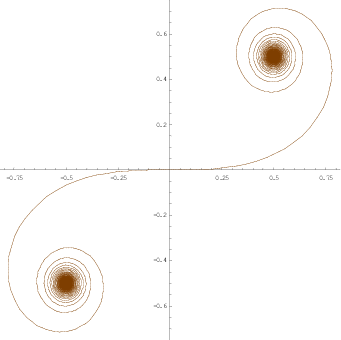 羊角螺线
羊角螺线
羊角螺线(clothoid),又称欧拉螺线(Euler spiral),是形式为


的曲线,其中 、
、 为 Fresnel积分:
为 Fresnel积分:


上面参数方程的参数 ,也是螺线于该点的曲率:
,也是螺线于该点的曲率: 。
。
两个螺线的中心位于
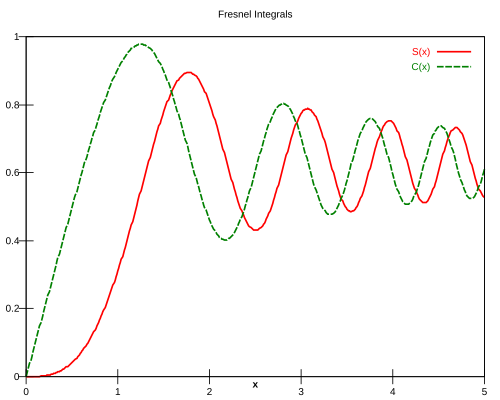
由于此螺线的曲率与长度成正比,故常用于公路工程或铁路工程,以缓和直路线与圆曲路线之间的曲率变化(向心力变化)。
在光学上,近场衍射(Fresnel衍射)中会应用Fresnel积分。
 和
和 是
是 的奇函数。
的奇函数。
 和
和 是整函数。
是整函数。
- 利用以上的幂级数展开式,可以把Fresnel积分扩展到复数范围,它是解析函数。Fresnel积分可以用误差函数来表示:

 .
.
 和
和 所定义的积分不能表示为初等函数。当
所定义的积分不能表示为初等函数。当 趋于无穷大时,函数的值为:
趋于无穷大时,函数的值为:
