相 (物质)
此条目需要补充更多来源。 (2023年6月) |

相(phase)亦称相态、物相(phase of matter)[1],是指某种或多种物质呈现某种物质状态时,若该物质或这些物质所占的体积(区域)内的分子均匀分布,则这片区域(体积)就是一个相。例如在玻璃罐中由冰和水组成的物理系统中,冰块是一相,水是一相,水蒸气也是一个相。罐子的玻璃是另一个相。
均相系又称单相系,是一种简单的系统,仅由一相所构成。更复杂的系统可能在某方面不均匀,这类系统称为非均相系或异相系。在做分析时,可以将非均相系统分为几个系统,每个系统都只具有一种相,都是均相系统[2]:86[3]:3。例如,经过仔细搅和后的溶液是均相系统,只具有一种相。又例如,在一个装有水和冰块的玻璃杯所组成的非均相系统中,水是一种相、冰块也是一种相,水上方的潮湿空气是另一种相,而玻璃杯又是另外一种相。
相和物质状态有时可以混同,有时可能有所区别,例如多个物质都处于同一物质状态(例如液体)时,可能会存在一种以上彼此不混溶的相(例如水和液态的油的物质状态都是液态,但两者不能互溶,是二个相)。相有时会用来描述由相图上的相边界划分出来的一组平衡状态;在这里,相边界是由像压力、温度一类的状态变数设定。相边界很重要地关联到在它两边的两种相所对比出的性质差异。例如,由液体变成固体、由某一种晶体结构变为另一种晶体结构。
相的分类
[编辑]
相可以用常见的物质状态来描述,像固态、液态和气态、等离子态、玻色-爱因斯坦凝聚态等。在固相与液相之间的中间相形成另一种物质状态,中间相物质是一种很有用的材料。但在同一个物质状态中也会存在不同的相,例如在铁-碳合金的相图中,存在许多物质状态都是固态或液态的各种不同的相,例如莱氏体、奥氏体、珠光体等。
在溶液里,溶质对于溶剂在溶解度方面的不同,使得可区分的相的出现成为可能,例如,水(极性分子)在油(非极性分子)中的溶解度很低,而油在水中的溶解度也很低,由水和油形成的混合物,因为二者不互溶,会自然分为二个相,并因此出现清楚的界面。两种物质的互溶度与它们彼此之间的的分子间作用力有关。一般而言,假若溶质A能够溶解于溶剂B,则在它们组成的溶液里,分子间吸引力KAB必须能克服KAA与KBB。分子间吸引力与分子的极性或非极性有关,例如,假若溶质A、溶剂B都是非极性物质,即KAA、KBB都很弱,而KAB也很弱,则溶质A在溶剂B的溶解度可能很高;假若溶质A、溶剂B都是极性物质,即KAA、KBB都很强,而KAB也很强,则溶质A在溶剂B的溶解度可能很高[4]:10-11。
类似的概念可以延伸到固体,固体可以形成固溶体,或者结晶形成不同的晶相。互溶的金属对(metal pair)可以形成合金;无法互溶的金属对不能形成合金。
举例而言,化学实验家已完成展示不互熔性的实验。在这实验里,可以观察到八种不互熔的相,一层一层的堆排在容器内 ,按照密度从小至大,分别为石蜡油、硅油、水、苯胺、全氟二甲基环己烷、熔融白磷、熔融镓、水银。在磷与镓都会熔化的温度45°C,这系统呈长久稳定平衡[4]:12。
不是所有有机溶剂都可以彼此互溶,例如乙二醇和甲苯都是有机溶剂,但会分为二个不同的相[5]。
有时候不同的相会自动分离,有清楚的界面,但有时不同的相不一定会有清楚的界面,像乳浊液和胶体都是不互溶的二相形成的混合物,但没有清楚的相边界。
2012年加拿大佩里米特理论物理研究所研究员文小刚在美国《科学》杂志的发表文章提出一种能够最终对相进行分类的新理论体系,物质有500多种相。该理论可以在任何维度、任何对称性的基础上对保有对称性的相实施构筑和分类。[6]
相平衡
[编辑]在相平衡时,许多的成分可能会形成均匀的一相,但单一相质也有可能在特定温度及压力下分为二个或三相不同的相,同一相的物理性质一样,但相和相之间的物理性质就不同了。
假设在密闭罐子中的水只占有一部分空间,则会形成两相,大部分的水是处于液相,靠水分子之间的吸引力而维持液相,但即使在相平衡时,分子仍然在运动,若某一个水分子获过够大的动能,就会打破水分子之间的吸引力,由液相变为气相,当一个水蒸气分子和水面碰撞,也会凝结成水。在平衡时,水蒸发和凝结的速度相同,液相及气相的体积都不会改变。
在室温及一般大气压力下,当罐中空气的湿度到3%时,水和水蒸气达到平衡。当温度升高,平衡时的湿度也会上升。在温度100%时,水会全部变成水蒸气时,若加热略超过100度,不只液体表面的水分子会气化,液体水整体都会气化,称为沸腾。
相的数量
[编辑]
给定一种组成,在特定温度及压力下只有某些相可以存在。相的数量及种类很难预估,一般都是用实验来求得,实验的结果会绘成相图。
右图是单一成分的相图,注意到系统的状相只和温度及压力有关,图中绘出两相或三相共存的条件,只要温度或压力偏离该条件,平衡状况下就只有一相。
图中的蓝线是液气共存的线段,但终止于一个称为临界点的温度及压力。当温度及压力接近临界点时,液相和气相的性质会越来接近,在临界点时无法区分液相和气相,温度及压力一旦超过临界点,就没有单独可区分的液相或气相,只会有一种称为超临界流体的流体相。水的临界点是647K(374 °C)及22.064MPa。
在水的相图中,一个特殊之处为其固液共存的线段(绿色点线)。对于大部分的物质,这条线的斜率为正值(绿色实线),表示若要维持固相和液相共存,温度升高,压力就大。但对于水这条线(绿色点线)的斜率为负值,这和冰的密度比水要低有关,将冰加压会使冰成为密度较高的相,也就是水。
另一个值得注意的特性是液气共存线、固液共存线彼此相交的点,称为三相点,在此温度及压力下,三相会共存
在实验方面,平衡线不难绘制,这是因为对于多相系统,温度与压力无关。试想由密闭隔温罐子与活塞组成的一个检试仪器,假设注入正确数量的水,加热,则这系统可以被带到相图的气相区域内的任意点。这时,假若用力将活塞缓慢推入罐子,则这系统会在相图的气相区域描绘出一条温度增加与压力增加的曲线。但是,假若这条曲线遇到液相-气相平衡线,即气体开始凝聚成液体的情况,则这系统之后描绘出的曲线会骤然地重叠于液相-气相平衡线,直到所有水汽体都凝聚成水液体。
界面现象
[编辑]在平衡的二相的边界之间,会有一狭窄区域,其性质和这二相都不同,虽然此区域可能非常狭窄,它可能造成显著与容易观测到的效应,例如促使液体展示出表面张力。混合物的某些成分可能比较喜欢移动至界面。为了建模、描述或了解某特定系统的物理行为,将界面区域视为独立分开的一相是个很好的点子。[3]:208-212
晶相
[编辑]同一种物质在固体时可能会有不止一种的相,以水为例,常见的冰是六边形的结构冰Ih,但也可能会有立方体的结构冰Ic、三方晶系的结构冰II以及其他的结构。
多形体是指一个固体有不只一种的晶体型式,由一种化学元素组成的多形体则称为同素异形体。例如石墨、钻石及富勒烯都是碳的同素异形体[7]。每一种多型体都是独立的晶相。
相变
[编辑]相变是指一物质由一个相转变为另一个相,
- 一级相变:当中会伴随着热量的吸收或释放,及体积、比热容、压缩率等会有变化[8]。例如水蒸发时,蒸发的水分子有较高的动能,因此液体的温度会下降。产生相变需要的能量(汽化热)要比将水由室温加热到沸点的能量要多,因此蒸发有助于冷却。相反的,凝结会放热。从固相变为液相的热能(或焓)变化称为熔化热,而由固相变为气相的热能(或焓)变化称为为升华热。
重要的相变还有氦-4在临界温度时Lambda相变为无粘滞的超流体、磁铁在居里温度从铁磁性变成顺磁性、金属-绝缘体相变、量子相变等。
进阶定义
[编辑]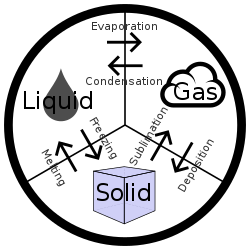
对自由能的分析
[编辑]虽然相的概念从表面上来看非常简单,但要对它作一个精确的定义却很困难。一个比较好的定义是一个相是一个在其范围内其热力学参数的自由能在参数空间中的函数是解析的。这个定义实际上就是说,假如两个系统是同一个相的话,那么在从一个系统转换到另一个系统的时候它们的热力学参数不会突然改变。
热力学中的参数如熵、热容量、压缩性等都可以被表示为自由能和它的导数。比如熵是自由能对温度的导数。只要自由能是解析的,那么热力学的其它参数也是连续的。
假如一个系统从一个相演变为另一个相,那么在这个过程中总会有一个阶段里自由能是不解析的。这个过程被称为相变。最常见的相变有溶化(从固态到液态)、冻结(从液态到固态)、蒸发(从液态到气态)和凝结(从气态到液态)。由于自由能在这个过程中是不解析的,因此在这个过程的两边它是两个完全不同的函数。两个相的热力学参数也完全不同。最显著的是热容量,在相变过程中热容量可以达到无穷大,从一个值跳到另一个值。
相关的热力学参数
[编辑]实际上每个相与另一个相之间总有一些相关的热力学参数非常不同。比如固体比液体要坚固得多,固体不像液体或气体那样,它可以保持它的形状。而液体则比气体的压缩性小得多。在一个大的容器中,气体可以充满整个容器,而液体则只占据一小部分。固体、液体和气体之间也有许多相同的热力学特性,比如它们的磁特性。但一个物质的铁磁态和顺磁态之间最大的区别就是它们的磁特性了。
另一个例子是同素异形体,许多物质在固态中可以有不同的晶体结构而具有非常不同的特性。钻石和石墨就是碳的同素异形体。从热力学的角度出发它们属于不同的相。
亚稳定的相
[编辑]亚稳定的状态有时也被看作是相,但精确地说它们并非相,因为它们不稳定。比如一些同素异形体只有在一定的条件下才稳定。取以上提及的碳为例,钻石只有在高压下才真正稳定。在一般的大气压和温度下钻石会缓慢地转变为石墨。但这个过程非常缓慢,因此在常温和常压下钻石是一种亚稳定的状态。假如温度加高的话,这个转化的过程就会加快。
相图
[编辑]一般人们用相图来表示一个系统的不同相。相图的轴是相关的热力学参数。简单的相图的轴是压强和温度。根据对应状态原理,使用约化坐标来绘制,所有简单物质的相图应该都很类似[3]:208-212[注 1]。
相图上的线被称为“相边界”,这是自由能不解析的地方,或者说相变发生的地方。而没有线的地方则是自由能解析的地方。这些地区属于同一个相。有些相的相边界不是在一切情况下都存在的。比如在647K和22.064兆帕斯卡以上水的液态和气态无法区分,液态和气态的相界在这个点就中断了。
形成和万能性
[编辑]相是一种宏观现象。组成一个系统的粒子数目假如比较少的话(一般少于1000)相的差别就消失了。其原因是只有在大的系统中系统的自由能才开始不解析。
相的另一个特性是它的万能性。不论一个宏观系统下的微观系统是怎样组成的,它们的相有非常类似的特性。比如铁和冰都是固态的,虽然从微观结构来说冰和铁的结构非常不同,但它们的固态都具有类似的特性,比如保持它们的形状。
相的分离
[编辑]在同一个系统中不同的相可以同时存在。一般来说它们之间有分明的边界,但也有例外,像乳浊液和胶体都是不互溶的二相形成的混合物,但没有分明的边界。
其中,
- ,表示系统的自由度,
- :系统的独立组元数
- :相数目
- :外界因素,多数取n=2,代表压力和温度。
若系统只有一种物质,,自由度 ,不一定为1,说明在系统中可以同时有几个相存在。在单一物质组成的系统中最多可以有三个相同时存在,但只有在一个特定的温度和压强下才有可能三个相同时存在(,表示温度和压强都是定值),这个点被称为三相点.[11]。两个相开始无法区分的点被称为临界点。在一定的温度或压强下也可能有两个相同时存在。假如一个系统由多种物质组成,那么也可能有更多的相同时存在。
参见
[编辑]注释
[编辑]参考资料
[编辑]- ^ Phases of Matter. NASA Official. [2024-05-13]. (原始内容存档于2024-09-09).
- ^ Enrico Fermi. Thermodynamics. Courier Corporation. 25 April 2012. ISBN 978-0-486-13485-7.
- ^ 3.0 3.1 3.2 3.3 Clement John Adkins. Equilibrium Thermodynamics. Cambridge University Press. 14 July 1983. ISBN 978-0-521-27456-2.
- ^ 4.0 4.1 Reichardt, C. Solvents and Solvent Effects in Organic Chemistry. Wiley-VCH. 2006: 9–10. ISBN 3-527-60567-3.
- ^ 此一现象有助于赫克反应中催化剂的回收再利用,参照Bhanage, B.M.; et al. Comparison of activity and selectivity of various metal-TPPTS complex catalysts in ethylene glycol — toluene biphasic Heck vinylation reactions of iodobenzene. Tetrahedron Letters. 1998, 39 (51): 9509–9512. doi:10.1016/S0040-4039(98)02225-4.
- ^ X. Chen, Z.-C. Gu, Z.-X. Liu, X.-G. Wen. Symmetry-Protected Topological Orders in Interacting Bosonic Systems. Science, 2012; 338 (6114): 1604 DOI: 10.1126/science.1227224
- ^ 成会明. 奈米碳管. 五南图书出版股份有限公司. 2004: 14–. ISBN 978-957-11-3499-4.
- ^ 近代物理学进展. 清华大学出版社有限公司. 1997: 166–. ISBN 978-7-302-02521-4.
- ^ Gibbs, J.W., Scientific Papers (Dover, New York, 1961)
- ^ Atkins, P.W.; de Paula, J. Physical chemistry 8th. edition. Oxford University Press. 2006. ISBN 0198700725. Chapter 6
- ^ International Union of Pure and Applied Chemistry (IUPAC), The IUPAC Compendium of Chemical Terminology,4-th ed. (The Gold Book) (1997)。在线校正版: (1994) "Triple point"。doi:10.1351/goldbook.T06502









