数据率失真理论(Rate distortion theory)或称信息率-失真理论(information rate-distortion theory)是信息论的主要分支,其的基本问题可以归结如下:对于一个给定的信源(source, input signal)分布与失真度量,在特定的码率下能达到的最小期望失真;或者为了满足一定的失真限制,可允许的最大码率为何,D 定义为失真的符号。
要完全避免失真几乎不可能。处理信号时必须允许有限度的失真﹐可减小所必需的信息率。1959年﹐Claude Shannon 首先发表《逼真度准则下的离散信源编码定理》一文,提出了率失真函数的概念。
失真函数能量化输入与输出的差异,以便进行数学分析。令输入信号为 ,输出信号为
,输出信号为 ,定义失真函数为
,定义失真函数为 ,失真函数可以有多种定义,其与到达域为非负实数:
,失真函数可以有多种定义,其与到达域为非负实数:
 。
。
汉明失真函数能描述错误率,定义为:
 ,
,
对汉明失真函数取期望即为传输错误率。
最常用于量测连续字符传输的失真,定义为:
 ,
,
平方误差失真函数不适用于语音或影像方面,因为人类感官对于语音或影像的平方误差失真并不敏感。
下列是率与失真(rate and distortion)的最小化关系函数:

这里 QY | X(y | x), 有时被称为一个测试频道 (test channel), 系一种条件概率之概率密度函数 (PDF),其中频道输出 (compressed signal) Y 相对于来源 (original signal) X, 以及 IQ(Y ; X) 是一种互信息(Mutual Information),在 Y 与 X 之间被定义为

此处的 H(Y) 与 H(Y | X) 是指信宿(output signal) Y 的熵(entropy)以及基于信源(source signal)和信宿(output signal)相关的条件熵(conditional entropy), 分别为:


这一样来便可推导出率失真的公式, 相关表示如下:
![{\displaystyle \inf _{Q_{Y|X}(y|x)}E[D_{Q}[X,Y]]{\mbox{subject to}}\ I_{Q}(Y;X)\leq R.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81c0d76dc68b9c8f50df630e3c6a6de7a42621d8)
这两个公式之间互为可逆推。
如果我们假设 PX(x) 服从正态分布且方差为σ2, 并且假设 X 是连续时间独立信号(或等同于来源无记忆或信号不相关),我们可以发现下列的率失真公式的“公式解”(analytical expression):
 [1]
[1]
下图是本公式的几何面貌:
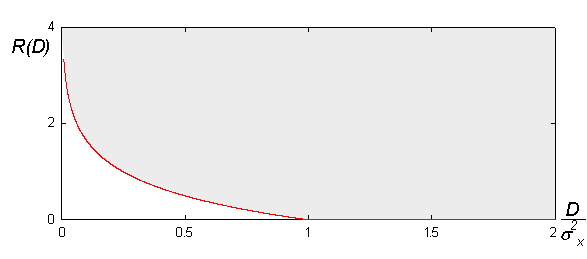
率失真理论告诉我们“没有压缩系统存在于灰色区块之外”。可以说越是接近红色边界,执行效率越好。一般而言,想要接近边界就必须透过增加码块(coding block)的长度参数。然而,块长度(blocklengths)的获取则来自率失真公式的量化(quantizers)有关。[1]
这样的率失真理论(rate–distortion function)仅适用于高斯无记忆信源(Gaussian memoryless sources)。
伯努利信源 ,
, ,以汉明失真描述的率失真函数为:
,以汉明失真描述的率失真函数为:

平行高斯信源的率失真函数为一经典的反注水算法(Reverse water-filling algorithm),我们可以找出一阈值 ,只有方差大于
,只有方差大于 的信源才有必要配置比特来描述,其他信源则可直接发送与接收,不会超过最大可容许的失真范围。
的信源才有必要配置比特来描述,其他信源则可直接发送与接收,不会超过最大可容许的失真范围。
我们可以使用平方误差失真函数,计算平行高斯信源的率失真函数。注意,此处信源不一定同分布:
 且
且 ,此时率失真函数为,
,此时率失真函数为,

其中,

且 必须满足限制:
必须满足限制:
 。
。
- ^ 1.0 1.1 Thomas M. Cover, Joy A. Thomas. Elements of Information Theory. John Wiley & Sons, New York. 2006.











![{\displaystyle \inf _{Q_{Y|X}(y|x)}E[D_{Q}[X,Y]]{\mbox{subject to}}\ I_{Q}(Y;X)\leq R.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81c0d76dc68b9c8f50df630e3c6a6de7a42621d8)










