泰勒锥

泰勒锥体是指在静电纺丝、电喷洒和流体动力喷雾过程中观察到的圆锥体,带电粒子射流从该过程中发出高于阈值电压的情形。
除了质谱中的电喷洒游离法,泰勒锥在电场发射的电推进和用于航天精细控制和高效推力的胶体推进器中也很重要。
历史
[编辑]在电喷洒被 “发现 ”之前,杰弗里·泰勒于1964年描述了这种圆锥形[1]
。这项研究是基于Zeleny的研究结果基础上进行的,以及其他几个人的研究,包含:Wilson和Taylor(1925)[2],Nolan(1926)[3]和麦基(1931)[4]。Zeleny拍摄了强电场中甘油的锥形喷射[2]。泰勒主要针对水滴在强电场中(例如:在暴雷雨中)的行为感兴趣。
形成
[编辑]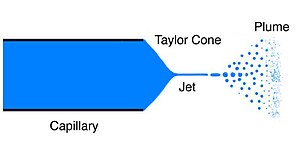
当少量的带电液体曝露在电场中,液体原有的形状因表面张力而产生变化。随着电压上升,电场的影响越显著。当电场的产生的效应在液滴上与表面张力的大小相似时,凸面和尖头的圆锥体因此形成,圆椎体的全角(宽度)接近 98.6° [1]。当达到特定电压阈值时,略微圆形的尖端翻转并喷射液体喷射流。这称为锥形喷射,是电喷洒过程的开始,使得离子可以转移至气相。为了达到稳定的锥形喷射,必须使用略高于阈值的电压。随着电压的的进一步增加,更多的液滴分散的模式被发现。“泰勒锥”一词,可特别指的是准确预测角度的完美锥体的理论极限;或者一般指电喷洒过程开始后的锥体喷射的接近锥形的部分。
理论
[编辑]在1964年,Geoffrey Ingram Taylor爵士描述了此现象,从理论上推导出的一般假设,即在这种条件下形成一个完美的圆锥体需要49.3°的半垂直角度(全角为98.6°),并证明了这种圆锥体的形状在喷射流形成之前就接近了理论形状。该角度被称之为泰勒角。这个角度跟准确来说是π- θ0,其中θ0为P1/2(cosθ0)的第一个0(1/2阶的勒尖得多项式)
Taylor的推导是基于两个假设:(1)圆锥体的表面是等位面的;(2)圆锥体是处于稳定平衡的状态。为了满足这两个标准,电场必须具有方位角对称性并具有依赖性,以对抗表面张力,从而产生圆锥体。解决方法如下:
其中V=V0(等位面)存在于θ0值处(与R无关)产生一个等位面的圆锥体。对于所有R而言,V=V0的必要角度是介于0和π之间的P1/2(cosθ0)的零点,而这一角度只有一个,即130.7099° 。这个角度的的余角即泰勒角。
参考
[编辑]- ^ 1.0 1.1 Sir Geoffrey Taylor. Disintegration of Water Droplets in an Electric Field. Proceedings of the Royal Society A. 1964, 280 (1382): 383–397. Bibcode:1964RSPSA.280..383T. JSTOR 2415876. doi:10.1098/rspa.1964.0151.
- ^ 2.0 2.1 Zeleny, J. The Electrical Discharge from Liquid Points, and a Hydrostatic Method of Measuring the Electric Intensity at Their Surfaces.. Physical Review. 1914, 3 (2): 69–91 [2022-05-18]. Bibcode:1914PhRv....3...69Z. doi:10.1103/PhysRev.3.69. (原始内容存档于2022-03-12).
- ^ Nolan, J. J. The Breaking of Water-Drops by Electric Fields. Proc. R. Ir. Acad. A. 1926, 37: 28 [2022-05-18]. (原始内容存档于2021-04-28).
- ^ Macky, W. A. Some Investigations on the Deformation and Breaking of Water Drops in Strong Electric Fields. Proceedings of the Royal Society A. October 1, 1931, 133 (822): 565–587. Bibcode:1931RSPSA.133..565M. doi:10.1098/rspa.1931.0168
 .
.


