在数学 和计算机科学 中,欧拉方法 (英语:Euler method [ 注 1] 数值 方法,用以对给定初值的常微分方程 [ 注 2]
欧拉方法是常微分方程数值方法 中最基本的显式方法 ;是一阶的方法,意味着其局部截断误差[ 注 3] 正比于 步长的平方,并且其全局截断误差正比于步长。[ 注 4]
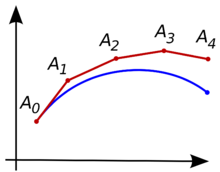
欧拉方法的图示。待求的曲线为蓝色,它的折线近似为红色。 考虑计算这样的一个未知曲线的形状:它具有给定的起点并且满足一个给定的微分方程。 这里,所谓“微分方程”可以看作能够通过曲线上任意点的位置而计算出这一点的切线 斜率 的公式。
思路是,一开始只知道曲线的起点(假设为
A
0
{\displaystyle A_{0}}
A
0
{\displaystyle A_{0}}
顺着切线向前走一小步到点
A
1
{\displaystyle A_{1}}
A
1
{\displaystyle A_{1}}
折线
A
0
A
1
A
2
A
3
…
{\displaystyle A_{0}A_{1}A_{2}A_{3}\dots }
图示为方程
y
′
=
y
,
y
(
0
)
=
1
{\displaystyle y'=y,y(0)=1}
中点法 ,红色为精确解
y
=
e
t
{\displaystyle y=e^{t}}
h
=
1.0
{\displaystyle h=1.0}
图示为同一个方程在步长
h
=
0.25
{\displaystyle h=0.25}
以以下微分方程为例
y
′
(
t
)
=
f
(
t
,
y
(
t
)
)
,
y
(
t
0
)
=
y
0
,
{\displaystyle y'(t)=f(t,y(t)),\qquad y(t_{0})=y_{0},}
希望用 y 在点 (t0 ,y(t0 )) 附近的线性近似来得到其近似解(也就是 y 的泰勒展开式 的前二项)。利用时间 t n 时的数值,若用单步的欧拉方法,可得到时间 t n+1 = t n + h 时的近似值如下:
y
n
+
1
=
y
n
+
h
f
(
t
n
,
y
n
)
.
{\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad }
欧拉方法是一种显型方法,也就是说
y
n
+
1
{\displaystyle y_{n+1}}
y
i
{\displaystyle y_{i}}
i
≤
n
{\displaystyle i\leq n}
欧拉方法可以求解一阶的微分方程,而任何
N
{\displaystyle N}
对于微分方程
y
(
N
)
(
t
)
=
f
(
t
,
y
(
t
)
,
y
′
(
t
)
,
…
,
y
(
N
−
1
)
(
t
)
)
{\displaystyle y^{(N)}(t)=f(t,y(t),y'(t),\ldots ,y^{(N-1)}(t))}
可以通过新设辅助变量
z
1
(
t
)
=
y
(
t
)
,
z
2
(
t
)
=
y
′
(
t
)
,
…
,
z
N
(
t
)
=
y
(
N
−
1
)
(
t
)
{\displaystyle z_{1}(t)=y(t),z_{2}(t)=y'(t),\ldots ,z_{N}(t)=y^{(N-1)}(t)}
z
′
(
t
)
=
(
z
1
′
(
t
)
⋮
z
N
−
1
′
(
t
)
z
N
′
(
t
)
)
=
(
y
′
(
t
)
⋮
y
(
N
−
1
)
(
t
)
y
(
N
)
(
t
)
)
=
(
z
2
(
t
)
⋮
z
N
(
t
)
f
(
t
,
z
1
(
t
)
,
…
,
z
N
(
t
)
)
)
{\displaystyle \mathbf {z} '(t)={\begin{pmatrix}z_{1}'(t)\\\vdots \\z_{N-1}'(t)\\z_{N}'(t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t)\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots ,z_{N}(t))\end{pmatrix}}}
这是一个以
z
(
t
)
{\displaystyle \mathbf {z} (t)}
[ 1]
设微分方程为
y
′
=
y
{\displaystyle y'=y}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
3
{\displaystyle y_{3}}
h
=
1
{\displaystyle h=1}
欧拉法为:
y
n
+
1
=
y
n
+
h
f
(
t
n
,
y
n
)
.
{\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).}
首先求
f
(
t
0
,
y
0
)
{\displaystyle f(t_{0},y_{0})}
n
=
0
{\displaystyle n=0}
f
{\displaystyle f}
f
(
t
,
y
)
=
y
{\displaystyle f(t,y)=y}
f
(
t
0
,
y
0
)
=
f
(
0
,
1
)
=
1.
{\displaystyle f(t_{0},y_{0})=f(0,1)=1.}
透过以上步骤,求得解曲线在点
(
0
,
1
)
{\displaystyle (0,1)}
y
{\displaystyle y}
t
{\displaystyle t}
Δ
y
/
Δ
t
{\displaystyle \Delta y/\Delta t}
接着是
h
⋅
f
(
y
0
)
=
1
⋅
1
=
1.
{\displaystyle h\cdot f(y_{0})=1\cdot 1=1.}
y
0
+
h
f
(
y
0
)
=
y
1
=
1
+
1
⋅
1
=
2.
{\displaystyle y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.}
重复以上步骤求出
y
2
{\displaystyle y_{2}}
y
3
{\displaystyle y_{3}}
y
2
=
y
1
+
h
f
(
y
1
)
=
2
+
1
⋅
2
=
4
{\displaystyle y_{2}=y_{1}+hf(y_{1})=2+1\cdot 2=4}
y
3
=
y
2
+
h
f
(
y
2
)
=
4
+
1
⋅
4
=
8
{\displaystyle y_{3}=y_{2}+hf(y_{2})=4+1\cdot 4=8}
由于欧拉法属于递归算法,把运算整理成表格也许有助于避免计算错误。
y
n
{\displaystyle y_{n}}
t
n
{\displaystyle t_{n}}
y
′
(
t
)
{\displaystyle y'(t)}
h
{\displaystyle h}
d
y
{\displaystyle dy}
y
n
+
1
{\displaystyle y_{n+1}}
1
0
1
1
1
2
2
1
2
1
2
4
4
2
4
1
4
8
欧拉法的局部截尾误差(Local truncation error, LTE)是指在实施一次欧拉法所产生的误差,是指经过一步的数值解
y
1
{\displaystyle y_{1}}
t
1
=
t
0
+
h
{\displaystyle t_{1}=t_{0}+h}
y
1
{\displaystyle y_{1}}
y
1
=
y
0
+
h
f
(
t
0
,
y
0
)
.
{\displaystyle y_{1}=y_{0}+hf(t_{0},y_{0}).\quad }
对于精确解,使用泰勒级数展开给出:
y
(
t
0
+
h
)
=
y
(
t
0
)
+
h
y
′
(
t
0
)
+
1
2
h
2
y
″
(
t
0
)
+
O
(
h
3
)
.
{\displaystyle y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}
欧拉法的局部截尾误差为:
L
T
E
=
y
(
t
0
+
h
)
−
y
1
=
1
2
h
2
y
″
(
t
0
)
+
O
(
h
3
)
.
{\displaystyle \mathrm {LTE} =y(t_{0}+h)-y_{1}={\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}
当
y
{\displaystyle y}
[ 2]
结果显示:当步长
h
{\displaystyle h}
h
2
{\displaystyle h^{2}}
龙格-库塔法 和线性多步法
h
p
{\displaystyle h^{p}}
p >2)成比例。
全局截尾误差(Global truncation error, GTE)是指在一个固定时间
t
{\displaystyle t}
[ 3]
(
t
−
t
0
)
/
h
{\displaystyle (t-t_{0})/h}
h
2
{\displaystyle h^{2}}
h
{\displaystyle h}
[ 4]
这个直观的推测可以被严谨地证明。如果解
y
{\displaystyle y}
f
{\displaystyle f}
y
{\displaystyle y}
利普希茨连续 的,那么全局截尾误差是有界的:
|
GTE
|
≤
h
M
2
L
(
e
L
(
t
−
t
0
)
−
1
)
{\displaystyle |{\text{GTE}}|\leq {\frac {hM}{2L}}(e^{L(t-t_{0})}-1)\qquad \qquad }
其中
M
{\displaystyle M}
y
{\displaystyle y}
L
{\displaystyle L}
f
{\displaystyle f}
[ 5]
这种精确的形式其实是没有什么意义的,通常情况下这个上界都会严重高估了欧拉法所造成的实际误差。[ 6]
h
{\displaystyle h}
[ 7]
Atkinson, Kendall A., An Introduction to Numerical Analysis 2nd, New York: John Wiley & Sons , 1989, ISBN 978-0-471-50023-0 Ascher, Uri M.; Petzold, Linda R., Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia: Society for Industrial and Applied Mathematics, 1998, ISBN 978-0-89871-412-8 Butcher, John C., Numerical Methods for Ordinary Differential Equations, New York: John Wiley & Sons , 2003, ISBN 978-0-471-96758-3 Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard, Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag , 1993, ISBN 978-3-540-56670-0 Iserles, Arieh, A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press , 1996, ISBN 978-0-521-55655-2 Lakoba, Taras I., Simple Euler method and its modifications (PDF) (Lecture notes for MATH334, University of Vermont), 2012 [2016-01-02 ] , (原始内容存档 (PDF) 于2012-07-12)