扭歪无限面体
外观

在几何学中,扭歪[1][2]无限面体(英语:Skew apeirohedron)是一种顶点并非全部共面的无限面体,存在非平面的面或非平面的顶点图,并保持图形不折回形成封闭区间而无限延伸。其也可以看作是面数无法被穷尽的扭歪多面体。由于该多面体所形成的空间有如海绵般有很多孔洞,因此又称为海绵多面体[3]。
正扭歪无限面体
[编辑]关于考克斯特,1926年时,约翰·弗林德斯·皮特里将扭歪多边形(非平面多边形)的概念推广到四维空间的扭歪多面体和三维空间的正扭歪无限面体[4]。
| 扭歪无限面体 | ||
|---|---|---|
 {4,6|4} 多立方体 四角六片四角孔扭歪无限面体 |
 {6,4|4} 多八面体 六角四片四角孔扭歪无限面体 |
 {6,6|3} 多四面体 六角六片三角孔扭歪无限面体 |
戈特的扭歪无限面体
[编辑]约翰·理查德·戈特在1976年时发表了一个较大的扭歪无限面体系列,该系列共有七种不同的扭歪无限面体,其中也包括了考克斯特和皮特里发现的那三种:{4,6}、{6,4}和{6,6},另外还多了四种{5,5}、{4,5}、{3,8}、{3,10}[5][6]。
| {p,q} | 胞 | 顶点附近的面 | 图像 | 空间群 | 相关的 H2 轨形 记号 | ||
|---|---|---|---|---|---|---|---|
| 立方 空间群 |
考克斯特 记号 |
纤维流形 记号 | |||||
| {4,5} | 立方体 |  |

|
Im3m | 8o:2 | *4222 | |
| {4,5} | 截角八面体 |  |
I3 | 80:2 | 2*42 | ||
| {3,7} | 正二十面体 |  |

|
Fd3 | 2o− | 3222 | |
| {3,8} | 正八面体 |  |

|
Fd3m | 2+:2 | 2*32 | |
| {3,8}[7] | 扭棱立方体 |  |

|
Fm3m | 2−− | 32* | |
| {3,9} | 正二十面体 |  |
I3 | 80:2 | 22*2 | ||
| {3,12} | 正八面体 |  |

|
Im3m | 8o:2 | 2*32 | |
半正扭歪无限面体
[编辑]亦存在其他的半正或均匀(点可递)的扭歪无限面体。瓦茨曼、伯特和克雷曼发现了许多例子[8],但他们不知道他们列出的列表是否完整。
| 4.4.6.6 | 6.6.8.8 | |
|---|---|---|

|

|

|
| 与大斜方截半立方体堆砌相关, |
与施莱夫利符号为h2,3{4,3,4}的几何图形相关, | |
| 4.4.4.6 | 4.8.4.8 | 3.3.3.3.3.3.3 |

|

|

|
| 与大斜方截角立方体堆砌相关, | ||
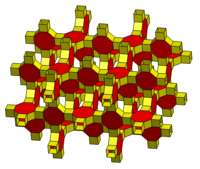
| 4.4.4.6 | 4.4.4.8 | 3.4.4.4.4 |

|
|
 与小斜方截半正方体堆砌相关, |
| 4.4.4.4.4 | 4.4.4.6 |
|---|---|
 与 |
 与 |
 
|

|
| 一种半正的曲面的几何结构 | 堆叠立方体 |
|---|
参见
[编辑]参考文献
[编辑]- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份,存于互联网档案馆)
- (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", Scripta Mathematica 6 (1939) 240-244.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 23, Objects with prime symmetry, pseudo-platonic polyhedra, p340-344)
- Schulte, Egon, Chiral polyhedra in ordinary space. I, Discrete and Computational Geometry, 2004, 32 (1): 55–99, MR 2060817, doi:10.1007/s00454-004-0843-x. [2] (页面存档备份,存于互联网档案馆)
- A. F. Wells, Three-Dimensional Nets and Polyhedra, Wiley, 1977. [3]
- E. Schulte, J.M. Wills On Coxeter's regular skew polyhedra (页面存档备份,存于互联网档案馆), Discrete Mathematics, Volume 60, June–July 1986, Pages 253–262
- ^ 400年ぶりに新種の「対称性多面体」構造が発見される. gigazine.net. 2014-02-22 [2016-07-16]. (原始内容存档于2020-11-19).
- ^ 扭歪の意味. Weblio日中中日辞典. [2024-04-23]. (原始内容存档于2013-07-20).
- ^ Michael Burt- Prof emeritus, Technion, I.I.T. Haifa Israel. Periodic Sponge Surfaces And Uniform Sponge Polyhedra In Nature And In The Realm Of The Theoretically Imaginable. 塞尔维亚科学与艺术学院. [2016-08-19]. (原始内容存档于2020-07-19).
- ^ Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- ^ J. R. Gott, Pseudopolyhedrons, American Mathematical Monthly, Vol 74, p. 497-504, 1967.
- ^ The Symmetries of things, Pseudo-platonic polyhedra, p.340-344
- ^ Richard Klitzing. Gott's snic-based pseudopolyhedron. 3D convex uniform polyhedra. bendwavy. [2021-10-16]. (原始内容存档于2021-09-30).
- ^ A. Wachmann, M. Burt and M. Kleinmann, Infinite polyhedra, Technion, 1974. 2nd Edn. 2005.
外部链接
[编辑]- 埃里克·韦斯坦因. Honeycombs and sponges. MathWorld.
- "Hyperbolic" Tessellations
- Infinite Regular Polyhedra (页面存档备份,存于互联网档案馆) [4] (页面存档备份,存于互联网档案馆)
- Infinite Repeating Polyhedra - Partial Honeycombs in 3-Space (页面存档备份,存于互联网档案馆)
- 18 SYMMETRY OF POLYTOPES AND POLYHEDRA, Egon Schulte: 18.3 REGULAR SKEW POLYHEDRA
- Infinite Polyhedra, T.E. Dorozinski

![{\displaystyle \left[\left[4,3,4\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0bb6a214d73a56bbfe67df20b3453c877fd8cd8)
![{\displaystyle \left[\left[4,3^{+},4\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/036fb3b636f4920ea46e7a6a74f9132350554a36)
![{\displaystyle \left[\left[3^{\left[4\right]}\right]\right]^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/533a56ea9573defe004f08115645ea930037f949)
![{\displaystyle \left[\left[3^{\left[4\right]}\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527e9b37f42db7b6b1f79fd1220519eef2612bbb)
![{\displaystyle \left[4,{\left(3,4\right)}^{+}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a595c7bf1c5fd4ac401c2a67e9202bda0823d2e)