 四阶第一类切比雪夫低通滤波器的频率响应图
四阶第一类切比雪夫低通滤波器的频率响应图
切比雪夫滤波器(又译柴比雪夫滤波器,英语:chebyshev filter),也被称为等涟波滤波器(equal ripple filter),是在通带或阻带上频率响应幅度等波纹波动的滤波器。在通带波动的为“I型切比雪夫滤波器”,在阻带波动的为“II型切比雪夫滤波器”。切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快,但频率响应的幅频特性不如后者平坦。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小,但是在通频带内存在幅度波动。
这种滤波器来自切比雪夫多项式,因此得名,用以纪念俄罗斯数学家巴夫尼提·列波维奇·切比雪夫(Пафнутий Львович Чебышёв)。
I型切比雪夫滤波器最为常见。
n阶第一类切比雪夫滤波器的幅度与频率的关系可用下列公式表示[1]:

其中:

- 而
 是滤波器在截止频率
是滤波器在截止频率 的放大率 (注意: 常用的以幅度下降3分贝的频率点作为截止频率的定义不适用于切比雪夫滤波器!)[来源请求]
的放大率 (注意: 常用的以幅度下降3分贝的频率点作为截止频率的定义不适用于切比雪夫滤波器!)[来源请求]
 是
是  阶切比雪夫多项式[2]:
阶切比雪夫多项式[2]:
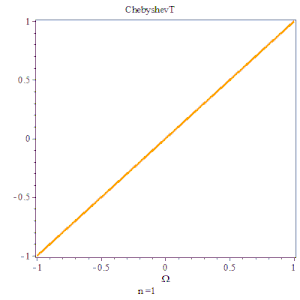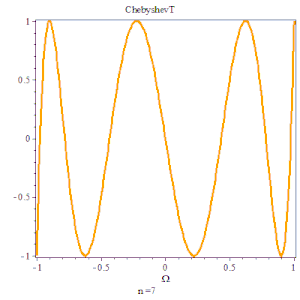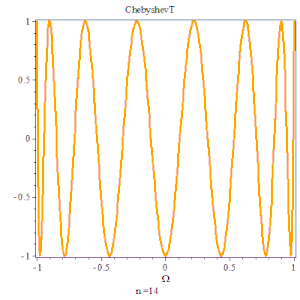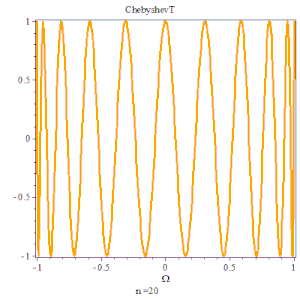 切比雪夫多项式
切比雪夫多项式


其中 
或:


| n |
切比雪夫多项式
|
| 0 |
1
|
| 1 |

|
| 2 |

|
| 3 |

|
| 4 |

|
| 5 |

|
| 6 |

|
| 7 |

|
| 8 |

|
| 9 |

|
| 10 |

|
切比雪夫滤波器的阶数等于此滤波器的电子线路内独立的电抗元件(或元件组)数。
切比雪夫滤波器的幅度波动 =  分贝
分贝
当  ,切比雪夫滤波器的幅度波动= 3分贝。
,切比雪夫滤波器的幅度波动= 3分贝。
如果需要幅度在在阻频带边上衰减得更陡峭,可允许在复平面的  轴上存在零点。但结果会使通频带内振幅波动较大,而在阻频带内对信号抑制较弱。 这种滤波器叫椭圆函数滤波器或考尔滤波器。
轴上存在零点。但结果会使通频带内振幅波动较大,而在阻频带内对信号抑制较弱。 这种滤波器叫椭圆函数滤波器或考尔滤波器。
也称倒数切比雪夫滤波器,较不常用,因为频率截止速度不如I型快,也需要用更多的电子元件。II型切比雪夫滤波器在通频带内没有幅度波动,只在阻频带内有幅度波动。
II型切比雪夫滤波器的转移函数为:

参数 ε 与 阻频带的 衰减度 γ 有如下关系:
 分贝。
分贝。
5分贝衰减度相当于ε = 0.6801; 10分贝衰减度相当于 ε = 0.3333。
截止频率 fC = ωC/2 π。
-3分贝频率fH 和截止频率 fC 有如下关系:

- 如果需要快速衰减而允许通频带存在少许幅度波动,可用第一类切比雪夫滤波器;如果需要快速衰减而不允许通频带存在幅度波动,可用第二类切比雪夫滤波器。
下图比较四种同阶低通滤波器:(左上)巴特沃斯滤波器、(右上)I型切比雪夫滤波器、(左下)II型切比雪夫滤波器(右下)椭圆函数滤波器。

两类切比雪夫滤波器比巴特沃斯滤波器陡峭; 但不如椭圆函数滤波器,然而后者幅度波动较大。
- ^ Rolf Schaumann et al, p295
- ^ Rolf Schaumann p295-298
- Rolf Schaumann,Haiqiao Xiao, Mac E.van Valkenburg, Analog Filter Design, 2nd Indian Edition, Oxford University Press, 2013
- Adel S. Sedra, Peter O. Brackett, Filter Theory and Design:Active and Passive, Matri Publishers Inc,1978






























