在数学 中,分数傅里叶变换 (Fractional Fourier transform,缩写:FRFT)指的就是傅里叶变换 (Fourier Transform)的广义化。近几年来,分数傅里叶变换除了在信号处理 领域有相当广泛的应用,其也在数学上被单独地研究,而定义出如分数回旋积分(Fractional Convolution)、分数相关(Fractional Correlation)等许多相关的数学运算。
分数傅里叶变换的物理意义即做傅里叶变换
a
{\displaystyle a}
a
{\displaystyle a}
时域 与频域 之间的分数域(Fractional Domain)。
若再更进一步地广义化分数傅里叶变换,则可推广至线性标准变换 。
对信号
x
(
t
)
{\displaystyle x(t)}
傅里叶变换 的结果为
F
(
x
)
{\displaystyle {\mathcal {F}}(x)}
傅里叶变换 的结果为
F
(
F
(
x
)
)
{\displaystyle {\mathcal {F}}({\mathcal {F}}(x))}
F
2
=
F
(
F
(
x
)
)
{\displaystyle {\mathcal {F}}^{2}={\mathcal {F}}({\mathcal {F}}(x))}
a
{\displaystyle a}
傅里叶变换 可以写成一般式
F
a
(
x
)
=
F
(
a
−
1
)
(
F
(
x
)
)
{\displaystyle {\mathcal {F}}^{a}(x)={\mathcal {F}}^{(a-1)}({\mathcal {F}}(x))}
a
{\displaystyle a}
a
=
2
ϕ
π
{\displaystyle a={\frac {2\phi }{\pi }}}
ϕ
=
1
2
a
π
{\displaystyle \phi ={\frac {1}{2}}a\pi }
x
(
t
)
{\displaystyle x(t)}
分数傅里叶变换 定义为
F
ϕ
(
x
)
=
F
2
ϕ
/
π
(
x
)
{\displaystyle {\mathcal {F}}_{\phi }(x)={\mathcal {F}}^{2\phi /\pi }(x)}
ϕ
{\displaystyle \phi }
分数傅里叶变换这个概念,其实最早在公元1929年,N.Wiener就已提出,但是并没有受到太多的瞩目。过了约莫50年,V.Namias 在公元1980年重新提出(称之为重发明)这个概念,但是一直到公元1994年,才有人真正把分数傅里叶变换用在信号处理上,此人为 L. B. Almeida。详细历史:1937年提出分数傅里叶变换的概念雏形; 1980年Namias较明确地提出分数傅里叶变换的数学表达式,并将其用于具有确定边界条件的量子力学薛定谔方程的求解1987年Bride & Kerr 给出严格的数学定义以及性质1993年由德国的学者罗曼,土耳其的Ozaktas和以色列的Mendlovic等人首次将分数傅里叶变换概念引入光学并给出了相应的光学过程; Mendlovic&Ozaktas:渐变折射率GRIN介质中光传播。 A. W. Lohmann: 维格纳分布函数和以及透镜实现,自由空间的光衍射。 1993年Ozaktas,罗曼,Mendlovic等人在光学中全面引入分数傅里叶变换; 1995年Shih提出了另外一种分数傅里叶变换的形式; 1997年刘树田等人根据Shih的定义给出了广义分数傅里叶变换,1999年刘树田等人将分数傅里叶变换应用于图像加密研究中; 2001年Ozaktas等人出版“分数傅里叶变换及其在光学和信号处理中应用”一书。
第一种定义:
X
ϕ
(
u
)
=
1
−
j
c
o
t
ϕ
⋅
e
j
π
⋅
c
o
t
ϕ
⋅
u
2
∫
−
∞
∞
e
−
j
2
π
⋅
c
s
c
ϕ
⋅
u
t
e
j
π
⋅
c
o
t
ϕ
⋅
t
2
x
(
t
)
d
t
{\displaystyle X_{\phi }(u)={\sqrt {1-jcot\phi }}\cdot e^{j\pi \cdot cot\phi \cdot u^{2}}\int _{-\infty }^{\infty }e^{-j2\pi \cdot csc\phi \cdot ut}e^{j\pi \cdot cot\phi \cdot t^{2}}x(t)dt}
第二种定义:
X
ϕ
(
u
)
=
1
−
j
c
o
t
ϕ
2
π
⋅
e
j
c
o
t
ϕ
2
⋅
u
2
∫
−
∞
∞
e
−
j
c
s
c
ϕ
⋅
u
t
e
j
c
o
t
ϕ
2
⋅
t
2
x
(
t
)
d
t
{\displaystyle X_{\phi }(u)={\sqrt {\frac {1-jcot\phi }{2\pi }}}\cdot e^{j{\frac {cot\phi }{2}}\cdot u^{2}}\int _{-\infty }^{\infty }e^{-jcsc\phi \cdot ut}e^{j{\frac {cot\phi }{2}}\cdot t^{2}}x(t)dt}
ϕ
=
0.5
a
π
{\displaystyle \phi =0.5a\pi }
a
{\displaystyle a}
当
a
=
1
{\displaystyle a=1}
ϕ
=
0.5
π
{\displaystyle \phi =0.5\pi }
分数傅里叶变换 就成了傅里叶变换 。
F
2
(
f
)
=
F
(
F
(
f
)
)
{\displaystyle {\mathcal {F}}^{2}(f)={\mathcal {F}}({\mathcal {F}}(f))}
F
(
n
+
1
)
(
f
)
=
F
(
F
n
(
f
)
)
{\displaystyle {\mathcal {F}}^{(n+1)}(f)={\mathcal {F}}({\mathcal {F}}^{n}(f))}
F
−
n
(
F
)
{\displaystyle {\mathcal {F}}^{-n}(F)}
F
(
ω
)
{\displaystyle F(\omega )}
n
{\displaystyle n}
F
−
1
(
F
)
{\displaystyle {\mathcal {F}}^{-1}(F)}
而分数傅里叶变换 将以上定义推广至非整数次的
n
=
2
α
π
{\displaystyle n={\frac {2\alpha }{\pi }}}
α
{\displaystyle \alpha }
实数 ,表示为
F
α
(
f
)
=
F
2
α
/
π
(
f
)
{\displaystyle {\mathcal {F}}_{\alpha }(f)={\mathcal {F}}^{2\alpha /\pi }(f)}
当
n
=
2
α
π
{\displaystyle n={\frac {2\alpha }{\pi }}}
n
{\displaystyle n}
例如:
n
=
1
{\displaystyle n=1}
傅里叶变换 ,如果在时频分析 (Time-Frequency Analysis)图上,则是对信号顺时针转90度
n
=
2
{\displaystyle n=2}
傅里叶变换 ,如果在时频分析 (Time-Frequency Analysis)图上,则是对信号顺时针转180度 ,
F
2
[
x
(
t
)
]
=
x
(
−
t
)
{\displaystyle {\mathcal {F}}^{2}[x(t)]=x(-t)}
n
=
3
{\displaystyle n=3}
傅里叶变换 ,如果在时频分析 (Time-Frequency Analysis)图上,则是对信号顺时针转270度
n
=
4
{\displaystyle n=4}
傅里叶变换 ,如果在时频分析 (Time-Frequency Analysis)图上,则是对信号顺时针转360度,
F
4
[
x
(
t
)
]
=
x
(
t
)
{\displaystyle {\mathcal {F}}^{4}[x(t)]=x(t)}
对于任一实数
α
{\displaystyle \alpha }
f
{\displaystyle f}
α
{\displaystyle \alpha }
F
α
(
f
)
(
ω
)
=
1
−
i
cot
(
α
)
2
π
e
i
cot
(
α
)
ω
2
/
2
∫
−
∞
∞
e
−
i
csc
(
α
)
ω
t
+
i
cot
(
α
)
t
2
/
2
f
(
t
)
d
t
{\displaystyle {\mathcal {F}}_{\alpha }(f)(\omega )={\sqrt {\frac {1-i\cot(\alpha )}{2\pi }}}e^{i\cot(\alpha )\omega ^{2}/2}\int _{-\infty }^{\infty }e^{-i\csc(\alpha )\omega t+i\cot(\alpha )t^{2}/2}f(t)dt}
并且具备以下特性
F
α
+
β
(
f
)
=
F
α
(
F
β
(
f
)
)
=
F
β
(
F
α
(
f
)
)
{\displaystyle {\mathcal {F}}_{\alpha +\beta }(f)={\mathcal {F}}_{\alpha }({\mathcal {F}}_{\beta }(f))={\mathcal {F}}_{\beta }({\mathcal {F}}_{\alpha }(f))}
F
α
[
∑
k
b
k
f
k
(
u
)
]
=
∑
k
b
k
F
α
[
f
k
(
u
)
]
{\displaystyle {\mathcal {F}}_{\alpha }\left[\sum \nolimits _{k}b_{k}f_{k}(u)\right]=\sum \nolimits _{k}b_{k}{\mathcal {F}}_{\alpha }\left[f_{k}(u)\right]}
若
α
=
k
π
2
{\displaystyle \alpha ={\frac {k\pi }{2}}}
k
{\displaystyle k}
k
{\displaystyle k}
当
α
=
π
2
{\displaystyle \alpha ={\frac {\pi }{2}}}
连续傅里叶变换 的定义 ,
当
α
=
−
π
2
{\displaystyle {\displaystyle \alpha ={\frac {-\pi }{2}}}}
连续傅里叶变换 之逆变换的定义。
若
α
{\displaystyle \alpha }
π
{\displaystyle \pi }
余切函数 和余割函数 不会收敛。
有一方法可解决此问题,就是取limit 让以上定义变成有一个狄拉克δ函数 被积分的情况,使得
F
α
=
F
k
π
2
=
F
k
=
(
F
)
k
{\displaystyle {\mathcal {F}}_{\alpha }={\mathcal {F}}_{\frac {k\pi }{2}}={\mathcal {F}}^{k}=({\mathcal {F}})^{k}}
(
F
α
)
−
1
=
F
−
α
{\displaystyle ({\mathcal {F}}_{\alpha })^{-1}={\mathcal {F}}_{-\alpha }}
F
α
1
F
α
2
=
F
α
2
F
α
1
{\displaystyle {\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}={\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{1}}}
(
F
α
1
F
α
2
)
F
α
3
=
F
α
1
(
F
α
2
F
α
3
)
{\displaystyle \left({\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}\right){\mathcal {F}}_{\alpha _{3}}={\mathcal {F}}_{\alpha _{1}}\left({\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{3}}\right)}
若从时频分析图上来看,代表的意义是在时频分析上旋转一角度后能量守恒
∫
f
∗
(
u
)
g
(
u
)
d
u
=
∫
f
α
∗
(
u
)
g
α
(
u
)
d
u
{\displaystyle \int f^{*}(u)g(u)du=\int f_{\alpha }^{*}(u)g_{\alpha }(u)du}
x
(
t
)
{\displaystyle x(t)}
ϕ
{\displaystyle \phi }
x
(
t
)
{\displaystyle x(t)}
维格纳分布 ,加伯变换 )顺时针旋转角度
ϕ
{\displaystyle \phi }
维格纳分布 (Wigner distribution function)[ 编辑 ] 假设
(a)
W
x
(
t
,
f
)
{\displaystyle W_{x}(t,f)}
x
(
t
)
{\displaystyle x(t)}
(b)
W
X
ϕ
(
u
,
v
)
{\displaystyle W_{X_{\phi }}(u,v)}
X
ϕ
(
u
)
{\displaystyle X_{\phi }(u)}
(c)
X
ϕ
(
u
)
{\displaystyle X_{\phi }(u)}
x
(
t
)
{\displaystyle x(t)}
,则
W
X
ϕ
(
u
,
v
)
=
W
x
(
u
c
o
s
(
ϕ
)
−
v
s
i
n
(
ϕ
)
,
u
s
i
n
(
ϕ
)
+
v
c
o
s
(
ϕ
)
)
{\displaystyle W_{X_{\phi }}(u,v)=W_{x}(ucos(\phi )-vsin(\phi ),usin(\phi )+vcos(\phi ))}
假设
(a)
G
x
(
t
,
f
)
{\displaystyle G_{x}(t,f)}
x
(
t
)
{\displaystyle x(t)}
(b)
G
X
ϕ
(
u
,
v
)
{\displaystyle G_{X_{\phi }}(u,v)}
X
ϕ
(
u
)
{\displaystyle X_{\phi }(u)}
(c)
X
ϕ
(
u
)
{\displaystyle X_{\phi }(u)}
x
(
t
)
{\displaystyle x(t)}
,则
G
X
ϕ
(
u
,
v
)
=
G
x
(
u
c
o
s
(
ϕ
)
−
v
s
i
n
(
ϕ
)
,
u
s
i
n
(
ϕ
)
+
v
c
o
s
(
ϕ
)
)
{\displaystyle G_{X_{\phi }}(u,v)=G_{x}(ucos(\phi )-vsin(\phi ),usin(\phi )+vcos(\phi ))}
例子一:
对一个加伯变换后的余弦函数 做不同角度的分数傅里叶变换。如下图
例子二:
对一个加伯变换后的矩形函数 做不同角度的分数傅里叶变换。如下图
可用分解信号和滤除噪声;一般来说分为两种,一种是在时域(Time domain)上,一种是在频域(Frequency domain)上,
这边利用分数傅里叶变换使其在分数域当中滤波。
假设现在
x
(
t
)
{\displaystyle x(t)}
x
(
t
)
=
x
1
(
t
)
+
x
2
(
t
)
{\displaystyle x(t)=x_{1}(t)+x_{2}(t)}
x
1
(
t
)
{\displaystyle x_{1}(t)}
x
2
(
t
)
{\displaystyle x_{2}(t)}
x
1
(
t
)
=
{
1
,
if
0
<
t
<
1
0
,
otherwise
{\displaystyle x_{1}(t)={\begin{cases}1,&{\mbox{if }}0<t<1{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}
x
2
(
t
)
=
{
1
,
if
8
<
t
<
10
0
,
otherwise
{\displaystyle x_{2}(t)={\begin{cases}1,&{\mbox{if }}8<t<10{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}
h
(
t
)
=
{
1
,
if
−
2
<
t
<
2
0
,
otherwise
{\displaystyle h(t)={\begin{cases}1,&{\mbox{if }}-2<t<2{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}
x
1
(
t
)
,
x
2
(
t
)
{\displaystyle x1(t),x2(t)}
若要将这两个信号分开,是非常简单的一件事情,因为这两个信号在时域上毫无重叠,便可以直接在时域上将这两个信号分开。
则
x
(
t
)
{\displaystyle x(t)}
h
(
t
)
{\displaystyle h(t)}
x
1
(
t
)
{\displaystyle x_{1}(t)}
x
2
(
t
)
{\displaystyle x_{2}(t)}
此作法可成功将这两个信号分开。
此种方法的限制为欲分解的信号必须在时域不能重叠,否则无法成功分解。
x
(
t
)
=
x
1
(
t
)
+
x
2
(
t
)
{\displaystyle x(t)=x_{1}(t)+x_{2}(t)}
x
1
(
t
)
=
s
i
n
(
4
π
t
)
{\displaystyle x_{1}(t)=sin(4\pi t)}
x
2
(
t
)
=
c
o
s
(
10
π
t
)
{\displaystyle x_{2}(t)=cos(10\pi t)}
可以很明显地看出
x
1
(
t
)
{\displaystyle x_{1}(t)}
x
2
(
t
)
{\displaystyle x_{2}(t)}
此时,可以妥善利用傅里叶变换将信号
x
(
t
)
{\displaystyle x(t)}
X
(
f
)
=
X
1
(
f
)
+
X
2
(
f
)
{\displaystyle X(f)=X_{1}(f)+X_{2}(f)}
X
1
(
f
)
=
δ
(
f
−
2
)
−
δ
(
f
+
2
)
2
{\displaystyle X_{1}(f)={\frac {\delta (f-2)-\delta (f+2)}{2}}}
X
2
(
f
)
=
δ
(
f
−
5
)
+
δ
(
f
+
5
)
2
{\displaystyle X_{2}(f)={\frac {\delta (f-5)+\delta (f+5)}{2}}}
由
X
(
f
)
{\displaystyle X(f)}
假设
H
(
f
)
{\displaystyle H(f)}
低通滤波器 (Low-pass Filter)
H
(
f
)
=
{
1
,
if
−
3
<
t
<
3
0
,
otherwise
{\displaystyle H(f)={\begin{cases}1,&{\mbox{if }}-3<t<3{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}
则
X
(
f
)
{\displaystyle X(f)}
H
(
f
)
{\displaystyle H(f)}
X
1
(
f
)
{\displaystyle X_{1}(f)}
X
2
(
f
)
{\displaystyle X_{2}(f)}
反之,若要保留
X
2
(
f
)
{\displaystyle X_{2}(f)}
X
1
(
f
)
{\displaystyle X_{1}(f)}
这种把欲处理信号先变换到频域,再做分解的动作,是滤波器设计的常见方法之一。
欲分解的信号必须在频域不能重叠,否则无法成功分解。
x
(
t
)
=
e
j
0.5
(
t
−
4
)
2
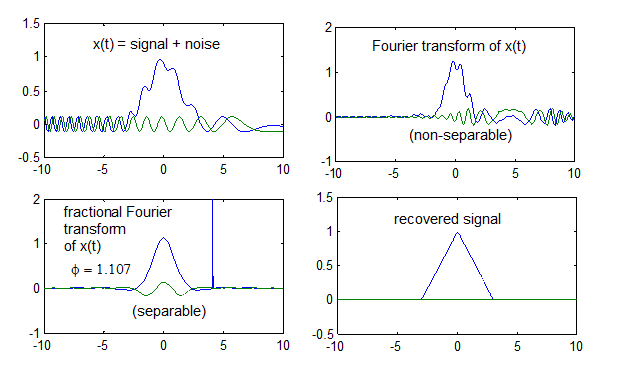
{\displaystyle x(t)=e^{j0.5(t-4)^{2}}}
啁啾 噪声) + 三角波信号。三角波信号(蓝色)是我们要的信号,将前面的啁啾(绿色)视为噪声,由图中可以发现到,
不论在时域或是频域,皆无法直接将噪音项
e
j
0.5
(
t
−
4
)
2
{\displaystyle e^{j0.5(t-4)^{2}}}
e
j
0.5
(
t
−
4
)
2
{\displaystyle e^{j0.5(t-4)^{2}}}
因此,对于两个在时、频域皆重叠的信号来说,很难在一维 的时域和频域中将其分解。
但若使用二维 的时频分析 ,则将有机会可以将两个在时、频域皆重叠的信号分解。
这是因为两个在时、频域皆重叠的信号其时频分布并不一定会重叠。因此,只要这两个信号的时频分布没有互相重叠,就可以善用分数傅里叶变换 将其成功分解(如下图左下、右下)。
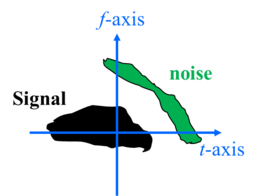
假设有噪音干扰,所以接收到的信号除了原始信号以外,还包含了噪声。
用时频分析方法来处理接收到的信号,黑色为原始信号(signal)的时频分布,而绿色为噪音(noise)的时频分布,如下图。
现在想把噪声滤掉,以下探讨3种方法来还原原始信号。
方法1 : 使用垂直的 Cutoff line
若在时频分布图中使用垂直的 Cutoff line ,就相当于在一维时域中,要把信号和噪音分离。
但是由下图可清楚看出,使用垂直的 Cutoff line 后,仍然会有一部分的噪音无法被去除。
因此方法1无法完美重建原始信号,而会有扭曲的情形发生。
方法2 : 使用水平的 Cutoff line
若在时频分布图中使用水平的 Cutoff line ,就相当于在一维频域中,要把信号和噪音分离。
但是由下图可清楚看出,使用水平的 Cutoff line 后,仍然会有一部分的噪音无法被去除。
因此方法2也无法完美重建原始信号,而会有扭曲的情形发生。
方法3 : 使用斜的 Cutoff line
若在时频分布图中使用斜的 Cutoff line ,则可以完美分离信号和噪音。如下图。
Cutoff line 的参数包含了
ϕ
{\displaystyle \phi }
u
0
{\displaystyle u_{0}}
ϕ
{\displaystyle \phi }
u
0
{\displaystyle u_{0}}
以下示范如何使用分数傅里叶变换和Cutoff line来将噪音滤除:
步骤(1) 首先决定cutoff line和纵轴f-axis的夹角
ϕ
{\displaystyle \phi }
步骤(2) 利用分数傅里叶变换对时频分布旋转
ϕ
{\displaystyle \phi }
步骤(3) 算出
u
0
{\displaystyle u_{0}}
步骤(4) 最后再做一次分数傅里叶变换
−
ϕ
{\displaystyle -\phi }
x
i
(
t
)
{\displaystyle x_{i}(t)}
x
o
(
t
)
{\displaystyle x_{o}(t)}
x
o
(
t
)
=
X
−
ϕ
[
X
ϕ
(
x
i
(
t
)
)
H
(
u
)
]
{\displaystyle x_{o}(t)=X_{-\phi }[{X_{\phi }(x_{i}(t))H(u)}]}
H
(
u
)
=
{
1
,
if
u
<
u
0
0
,
if
u
>
u
0
{\displaystyle H(u)={\begin{cases}1,&{\mbox{if}}u<u_{0}{\mbox{ }}\\0,&{\mbox{if}}u>u_{0}{\mbox{ }}\end{cases}}}
例子二: 假设发射一信号s(t),中间受到噪声干扰,最后收到的信号为f(t)=s(t)+noise
(a) 发射信号的时域图
(b) 接收信号的时域图
(c) 发射信号的韦格纳分布
(d) 接收信号的韦格纳分布,有由此可见cross-term已经大大的影响时频图的可见姓,加上噪声后的韦格纳分布更是无法清楚地将信号分离开来
(e) 发射信号的加伯变换
(f) 接收信号的加伯变换
(h) 滤波器的设计,这边总共有四条cutoff lines,其中有两条平行,所以总共需要做三次不同的分数傅里叶变换,再借由cutoff lines来去除噪声
(i) 滤波器的设计,这边总共有四条cutoff lines,其中有两条平行,所以总共需要做三次不同的分数傅里叶变换,再借由cutoff lines来去除噪声
(j) 对(i)做分数傅里叶变换
(k) 利用高通滤波器滤波,把两条cutoff lines设置在低频
(l) 经过(k)滤波器以后
(m) 透过同上的手法再做两次低通滤波器,把旁边两条线给去除后可得到的还原信号
(n) 发射信号(蓝色)和还原信号(绿色)的比较,两者的MSE仅有0.1128% 由以上可知,透过分数傅里叶旋转时频图的技巧来设计滤波器,我们可以精准地还原信号
例子三:
一样假设接收信号受到了噪声干扰
(a) 发射信号
(b) 接收信号
(c) 接收信号的韦格纳分
(d) 接收信号的加伯变换
(e) 接收信号的加伯-维格纳变换,在这边的滤波器需要五条cutoff lines(蓝线),但有两条是垂直时间轴,可以直接在时间轴上去除,剩下的三条则需要利用分数傅里叶变换来去除。
(f) 还原信号,MSE仅0.3013%
傅里叶变换
优点: 运算复杂度较低,有快速傅里叶变换的算法。
缺点: 仅有一个维度,频域,来分析;噪声若和信号重叠,则难以分离。
分数傅里叶变换
优点: 运用旋转的技巧在时频图上去除噪声,多了一个维度(时域)来分析;除非噪声和信号同时在频域和时域上重叠,否则将可以分离两信号。
缺点: 运算复杂度较高。
其他的时间-频率变换:
N. Wiener, "Hermitian polynomials and Fourier analysis," Journal of Mathematics Physics MIT , 18 , 70-73 (1929).
V. Namias, "The fractional order Fourier transform and its application to quantum mechanics," J. Inst. Appl. Math. 25 , 241–265 (1980).
Luís B. Almeida, "The fractional Fourier transform and time-frequency representations," IEEE Trans. Sig. Processing 42 (11), 3084–3091 (1994).
Soo-Chang Pei and Jian-Jiun Ding, "Relations between fractional operations and time-frequency distributions, and their applications," IEEE Trans. Sig. Processing 49 (8), 1638–1655 (2001).
D. H. Bailey and P. N. Swarztrauber, "The fractional Fourier transform and applications," SIAM Review 33 , 389-404 (1991). (Note that this article refers to the chirp-z transform variant, not the FRFT.)
Haldun M. Ozaktas, Zeev Zalevsky and M. Alper Kutay. "The Fractional Fourier Transform with Applications in Optics and Signal Processing". John Wiley & Sons (2001). Series in Pure and Applied Optics.
Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2013 
































![{\displaystyle {\mathcal {F}}^{2}[x(t)]=x(-t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/642fb7430630068ae31dbdc0aba8ef9d0210b495)


![{\displaystyle {\mathcal {F}}^{4}[x(t)]=x(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616604e6dbaf6e1e8ac3f5b09da2b1475da7602f)



![{\displaystyle {\mathcal {F}}_{\alpha }\left[\sum \nolimits _{k}b_{k}f_{k}(u)\right]=\sum \nolimits _{k}b_{k}{\mathcal {F}}_{\alpha }\left[f_{k}(u)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9c99656b0433c3cb3cc57ba016f25865c872d61)













































![{\displaystyle x_{o}(t)=X_{-\phi }[{X_{\phi }(x_{i}(t))H(u)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bc271b5a6f80d070ff91fc676b7775704c92e52)




