在数学中,考克斯特群是一类由空间中对超平面的镜射生成的群。这类群广泛出现于数学的各分支中,二面体群与正多胞体的对称群都是例子;此外,根系对应到的外尔群也是考克斯特群。这类群以数学家哈罗德·斯科特·麦克唐纳·考克斯特命名。
所谓考克斯特群,是一个群  写成如下的表达式,即由满足一些交互关系的生成元生成的群
写成如下的表达式,即由满足一些交互关系的生成元生成的群

其中  满足
满足  以及
以及  对所有
对所有  。在此
。在此  意指
意指  恒不等于单位元。
恒不等于单位元。
注意到  ;若
;若  ,则
,则  。且 m 满足对称性
。且 m 满足对称性  。
。
令这组生成元为  。资料
。资料  称为考克斯特群。方阵
称为考克斯特群。方阵  称为考克斯特矩阵。
称为考克斯特矩阵。
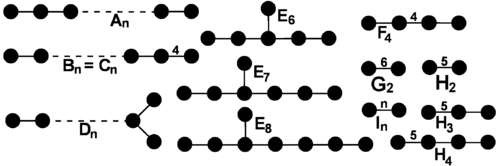 有限考克斯特群的分类
有限考克斯特群的分类
设  为考克斯特群,可证明存在一个有限维实矢量空间
为考克斯特群,可证明存在一个有限维实矢量空间  及其上的非退化双线性形
及其上的非退化双线性形  (未必正定),使得
(未必正定),使得  同构于正交群
同构于正交群  的某个子群。由于
的某个子群。由于  的元素均为二阶,可视之为
的元素均为二阶,可视之为  中对某些超平面的镜射。
中对某些超平面的镜射。
利用  的展示,定义元素的长度如下:对
的展示,定义元素的长度如下:对  ,定义其长度
,定义其长度  为所有表法
为所有表法  中最短的
中最短的  。由此可导出
。由此可导出


- 对称群
 是考克斯特群。在此可取
是考克斯特群。在此可取  为置换
为置换  ;关系为
;关系为  。
。
- 正多胞体的对称:正多胞体的对称群是有限考克斯特群。举例明之:正多边形的对称群是二面体群,正 n 维单形的对称群是前述的
 ,又称为
,又称为  型的考克斯特群。n 维超正方体的对称群为
型的考克斯特群。n 维超正方体的对称群为  。正十二面体与正二十面体的对称群是
。正十二面体与正二十面体的对称群是  。在四维空间中,存在三种特别的正多胞体──正二十四胞体、正一百二十胞体与正六百胞体,其对称群分别是
。在四维空间中,存在三种特别的正多胞体──正二十四胞体、正一百二十胞体与正六百胞体,其对称群分别是  。
。 可以由某些半正多胞体的对称群得到。
可以由某些半正多胞体的对称群得到。
- 仿射外尔群:仿射外尔群是无限群,但带有一个正则阿贝尔子群,使得对应的商群是个外尔群。
一般而言,两个群展示的同构与否是无法判定的。然而对考克斯特群则有一个简单的判准,称为交换条件。可以透过考克斯特-丹金图分类有限考克斯特群。图的构造方式为:
- 每个生成元对应到一个顶点。
- 若
 ,则顶点
,则顶点  之间有边相连。
之间有边相连。
- 若
 ,则将边标上
,则将边标上  。
。
- Larry C Grove and Clark T. Benson, Finite Reflection Groups (1985), Graduate texts in mathematics, vol. 99, Springer.
- Paul Garrett, Buildings and Classical Groups (1997), Chapman Hall. ISBN 0-412-06331-X . PostScript 档案下载 (页面存档备份,存于互联网档案馆) .
- James E. Humphreys, Reflection Groups and Coxeter Groups (1990), Cambridge studies in advanced mathematics, 29.







































