分子振动
外观
(重定向自振動態)
分子振动是指分子内原子间进行的周期性来回运动,而不包含分子的移动和转动。这种周期性的运动频率称为振动频率。在光谱学上常用红外吸收光谱法与拉曼光谱学来测量分子的振动频率,并用来分析分子结构。
振动座标系
[编辑]一个拥有 n 个原子的非线性分子有 3n − 6 个振动正交模(vibrational normal mode),其余为 3 个转动、3 个移动。而线性的分子有 3n − 5 个振动正交模,只有 2 个转动[1]。双原子分子为线性分子,所以有一个振动模。每一振动正交模有其不同的振动频率。分子的振动正交模可透过群论的点群来分析[2]。
范例
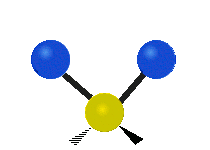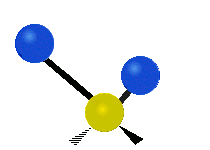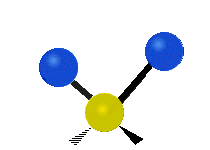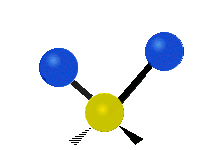
[编辑]以乙烯 (C2H4) 作为例子,C2H4 有 6 × 3 − 6 = 12 个振动模:

其中,有 4 个 C-H 伸展 (stretching)、1 个 C=C 伸展、2 个 H-C-H 剪式运动 (scissoring)、1 个 H-C-H 摆动 (rocking)、1 个 C-C-H 摆动、2 个 H-C-H 摇摆 (wagging)与1 个 H-C-H 扭转 (twisting)。在摆动、摇摆与扭转模,原子间的键长不会改变。
| 对称伸展 | 不对称伸展 | 平面剪式运动 |
|---|---|---|
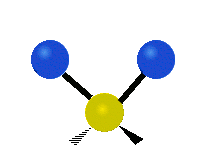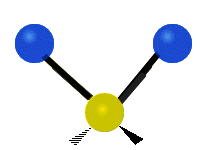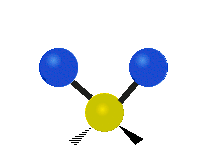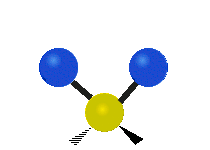
|
|

|
| 平面摆动 | 非平面摇摆 | 非平面扭转 |
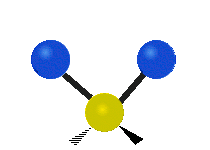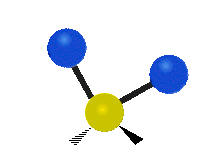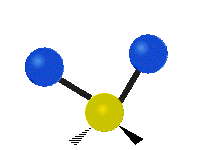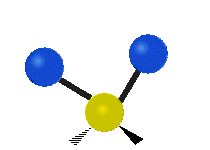
|

|
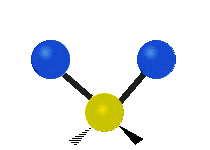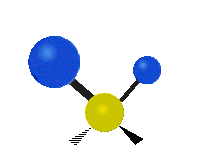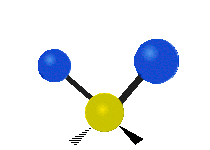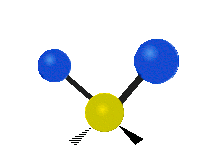
|
乙烯的对称性属于 D2h 点群,下表列出其 12 个振动正交模及其对应点群的不可约表示 (irreducible representation )、频率及红外(Infrared active,IR active)与拉曼活性(Raman active):
| 振动正交模 | 不可约表示 | 频率 | 红外活性 | 拉曼活性 |
|---|---|---|---|---|
| C-H 对称伸展 | b1u | 3217 cm-1 | 是 | 否 |
| C-H 对称伸展 | ag | 3210 cm-1 | 否 | 是 |
| C-H 不对称伸展 | b2u | 3185 cm-1 | 是 | 否 |
| C-H 不对称伸展 | b3g | 3153 cm-1 | 否 | 是 |
| C-C 对称伸展 | ag | 1827 cm-1 | 否 | 是 |
| H-C-H 平面剪式运动 | b1u | 1413 cm-1 | 是 | 否 |
| H-C-H 平面剪式运动 | ag | 1388 cm-1 | 否 | 是 |
| C-C-H 平面摆动 | b3g | 1167 cm-1 | 否 | 是 |
| H-C-H 非平面摇摆 | b3u | 1068 cm-1 | 是 | 否 |
| H-C-H 非平面摇摆 | b2g | 1057 cm-1 | 否 | 是 |
| H-C-H 非平面扭转 | au | 875 cm-1 | 否 | 否 |
| H-C-H 平面摆动 | b2u | 835 cm-1 | 是 | 否 |
量子化学
[编辑]在处理正交振动模时,量子化学使用简谐运动来近似处理分子振动。解薛定谔方程式可获得以下的振动能阶公式:
其中 n 为振动量子数 0, 1, 2,...,可用来代表其振动能阶、振动量子态,详细推导请参阅量子谐振子。
参阅
[编辑]参考文献
[编辑]- ^ Landau LD and Lifshitz EM (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover)
- ^ Cotton, F. A., Chemical Applications of Group Theory, John Wiley & Sons: New York, 1990. ISBN 0471510947

