德劳内三角剖分

一个平面德劳内三角化的例子，所有三角形外接圆以灰色表示。

在数学和计算几何领域，平面上的点集P的德劳内三角剖分（英语：Delaunay triangulation）是一种是点P的一个三角剖分DT，使在P中没有点严格处于 DT(P) 中任意一个三角形外接圆的内部。德劳内三角剖分最大化了此三角剖分中三角形的最小角，换句话，此算法尽量避免出现“极瘦”的三角形。此算法命名来源于鲍里斯·德劳内，以纪念他自1934年在此领域的工作。

与沃罗诺伊图的关系

若一离散点集的点均处于一般位置，则德劳内三角化就对应到沃罗诺伊图的对偶。特殊情形包括了三点共线及四点共圆

• 
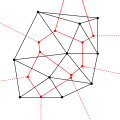
  一个德劳内三角化的例子，所有三角形外接圆的圆心以红点表示。
• 
  连接外接圆圆心即产生沃罗诺伊图，在此以红线表示。