数据选择器

在电子技术(特别是数字电路)中,数据选择器(英语:Data Selector),或称多路复用器(英语:multiplexer,简称:MUX[1]),是一种可以从多个模拟或数字输入信号中选择一个信号进行输出的器件。[2] 一个有 2n 输入端的数据选择器有 n 个可选择的输入-输出线路,可以通过控制端来选择其中一个信号被选择作为输出。[3] 数据选择器主要用于增加一定量的时间和带宽内的可以通过网络发送的数据量。[2]
数据选择器使多个信号共享一个设备或资源,例如一个模拟数字转换器或一个传输线,而不必给每一个输入信号配备一个设备。
结构图
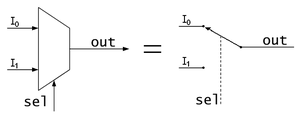
[编辑]在结构图中,数据选择器的符号是一个等腰梯形,其中较长的底上为数个输入引脚,较短的底上为一个输出引脚。右图即为一个2选1数据选择器的结构图和其等效简化图。Sel引脚可以选择需要的信号。
此外,在很多数据选择器里,还有一个“使能”引脚用于控制器件的有效或者无效[4]。
数字电路中的应用
[编辑]在数字电路设计中,选择端的输入信号是数字信号。在2选1数据选择器的例子中,选择端输入低电平0,则输出引脚会输出上的输入信号;反之,当选择端输入高电平1,则输出引脚会输出上的输入信号。当输入引脚的数目更多时,情况与上面类似,不过所需的选择端引脚数目变为个,这里是输入引脚的个数。

一个2选1数据选择器有如下的布尔函数,和分别表示两个输入信号,为选择信号,为输出信号,则有
注意,并非所有的逻辑函数直接具有以上的形式,但是所有的逻辑函数都可以使用香农展开(Shannon's expansion)的方法将它变换为上面这种形式。逻辑函数可以用下面的真值表表示:
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 0 | 0 | |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 0 | 0 |
这个真值表显示,当,那么;而当,则。在具体的电路中,实现一个这样的2选1数据选择器需要2个与门、一个或门和一个非门。
更大型的数据选择器也较常见,而且正如上面描述的,个输入引脚需要个选择引脚。其他常见的类型有4选1、8选1和16选1等。由于数字逻辑采用二进制的数字信号,输入引脚的个数通常是2的幂。
-
4选1数据选择器
-
8选1数据选择器
-
16选1数据选择器
4选1数据选择器的布尔函数如下:
这样的数据选择器可以由如下的电路实现:
| |||
芯片的级联
[编辑]大型的数据选择器可以由较小的数据选择器级联来实现[5]。例如,一个8选1数据选择器可以由两个4选1数据选择器组成,一个4选1数据选择器可以由两个2选1数据选择器组成。在前者中,两个4选1选择器的输出端连接到2选1选择器,并且两个4选1选择器和一个2选1选择器的选择端的引脚平行地接出,视为“8选1数据选择器”的“3个选择引脚”。
数据选择集成芯片
[编辑]7400系列有若干种集成电路具有数据选择器功能,列表如下[6]:
| IC 芯片代号 | 功能 | 输出状态 | |
|---|---|---|---|
| 1 | 74157 | 四2选1数据选择器 | 输出原变量 |
| 2 | 74158 | 四2选1数据选择器 | 输出反变量 |
| 3 | 74153 | 双4选1数据选择器 | 输出原变量 |
| 4 | 74352 | 双4选1数据选择器 | 输出反变量 |
| 5 | 74151A | 8选1数据选择器 | 输出原变量/反变量 |
| 6 | 74151 | 8选1数据选择器 | 输出反变量 |
| 7 | 74150 | 16选1数据选择器 | 输出反变量 |
数据选择器作为可编程逻辑器件
[编辑]数据选择器同样可被用作可编程逻辑器件。通过指定输入信号的排列,用户可以创建一个定制的逻辑电路。选择引脚充当了逻辑输入的功能。当生产成本和模块化有限的时候,这种方式十分有用。
在硬件描述语言中,可以采用数据流或者行为语句对数据选择器进行描述。例如,在Verilog中,可以使用条件运算符条件?表达式1:表达式2或者使用if条件结构或case选择结构来实现数据选择器。
参考文献
[编辑]- ^ What is a Multiplexer. wiseGEEK. [2011-04-22]. (原始内容存档于2011-04-23).
- ^ 2.0 2.1 Dean, Tamara. Network+ Guide to Networks. Delmar. 2010: 82–85 [2015-04-04]. (原始内容存档于2014-07-08).
- ^ Debashis, De. Basic Electronics. Dorling Kindersley. 2010: 557 [2015-04-04]. (原始内容存档于2014-02-22).
- ^ 刘宝琴、王德生、罗嵘. 逻辑设计与数字系统. 北京: 清华大学出版社. : 61页. ISBN 978-7-302-09320-6 (中文(中国大陆)).
- ^ 刘宝琴、王德生、罗嵘. 逻辑设计与数字系统. 北京: 清华大学出版社. : 62页. ISBN 978-7-302-09320-6 (中文(中国大陆)).
- ^ 7400 Series Description. capetronics.com. (原始内容存档于2010-02-13).
- M. Morris Mano; Charles R. Kime. Logic and Computer Design Fundamentals 4. Prentice Hall. 2008. ISBN 013198926X (英语).




















