可压缩流

可压缩流是一种气流，而且此类气流密度会出现显着变化。尽管所有气流都是可压缩的，但是当马赫数（流速与声速的比值）小于0.3时，因为速度造成的密度变化通常小于5%，此时气流会视为不可压缩流。 可压缩流的研究与高速飞机、喷气发动机、火箭发动机、高速进入行星大气、天然气管道、商业应用（例如喷砂处理）以及许多其他领域有关。

历史

气体动力学研究与航天发展息息相关，现代飞机的高速飞行、太空飞行器的大气重返等问题，以往都未曾深入研究。但其实早在19世纪初，就曾有分析发射子弹气体改变，从而提高了枪支和大炮的准确性和能力。 随着时间推移，诸如古斯塔夫·拉伐尔等发明家推动了这一领域的发展，而诸如恩斯特·马赫(Ernst Mach)等研究人员则试图透过实验来了解所涉及的物理现象。

20世纪初，气体动力学的研究重点转移到了航空领域。路德维希·普朗特和他的学生提出了重要的概念，从边界层到超音速激波，超音速风洞和超音速喷嘴设计。 普朗特大学的学生西奥多·冯·卡门继续提高对超音速流动的理解。其他著名人物：西奥多·梅耶、Luigi Crocco和Shapiro，也为现代气体动力学研究基础做出了重要贡献。

随着20世纪初期人们对气体动力学的理解提高，人们误以为飞机最高速度存在障碍，通常会称为音障 。事实上，超音速飞行的障碍只有当时尚不成熟的技术。当气流接近声速时，常规翼型的阻力系数显着增加，在当代很难克服高马赫数产生的大阻力，因此“音障”此一概念于焉诞生。好在飞机设计最终大幅进步，可以生产出Bell X-1 。由查克·叶格(Chuck Yeager)驾驶的X-1于1947年10月正式实现了超音速。

纵观历史，科学家们研究气体动力学的进程中，分成两条平行的路径。实验气体动力学，进行风洞模型实验以及在激波管和弹道实验，并使用光学影像技术记录新的发现。理论气体动力学，则以理论分析应用于可变密度气体的运动方程式及其解。许多基本的气体动力学是解析性的，意即一般人可用公式算得解析解，但是在现代，计算流体动力学(Computational Fluid Dynamics)应用电脑计算来解决特定几何形状和可压缩流间，原本棘手的非线性偏微分方程，即所谓数值解。

基本概念

流体力学及其分支

可压缩流的基础理论涉及几个重要的假设：

1. 连续性：所有流体都是由分子组成的，但是不必跟着气流（例如在大气压下）中大量的分子单体。借由假设气流连续，我们可以将气流视为低密度的连续物质。只有在高层大气、太空等低密度的领域中，单一分子的运动才变得重要。
2. 无滑动条件：假定固体表面的流速等于表面本身的速度，这是假设连续流动的直接结果。无滑动条件意味着流动具有粘性，而也意味着空气的高速流动，会在物体上形成边界层。

不可压缩流问题大多仅涉及两个未知数：压力和速度，通常仅须透过两个方程式即可求得，方程式描述了质量守恒和线性动量守恒，且流体密度假定为常数。但是，在可压缩流中，气体密度和温度也成为变量。为了解决可压缩流问题，这需要两个以上的方程：气体的状态方程和能量守恒方程。对于大多数气体动力学问题，理想气体是合理且适当的状态假设。

流体力学问题有两种做法：拉格朗日法和欧拉法。拉格朗日法在流过流场时遵循特定一块流体质量。反之，欧拉法则不会随流体一起移动，而是固定观察流体流过的同一块框架或控制体积。虽然拉格朗日法才能看出一个流体如何从前面这样变成后面那样，然而实务上不太可能做到这件事，因此做实验通常采用欧拉法来观察。

最后，尽管已知空间具有3个维度，但是如果仅其中一维具有最重要的意义，则在数学上描述气流时可以进行重要的简化：假定为单维流动。这在计算管路、喷嘴和扩散器的流动时非常有用，因为在这些流动中，流动特性主要只在轴向而非侧向上改变。但是计算高速运动物体上的外部流时，至少需要看成二维。当三个空间维度（也许还有时间维度）都很重要时，大概就要求助电脑来算了。

马赫数，波动和声速

马赫数(M)定义为速度与声速之比。例如，在室温下，声音经由空气传播的速度约为340 m/s（1,100 ft/s） 。 M值的范围可以从0到∞，但是这种宽泛的范围又可细分为：亚音速、跨音速、超音速、超高音速和超高速流。下图是马赫数光谱，可看到他们如何分布。

马赫数光谱

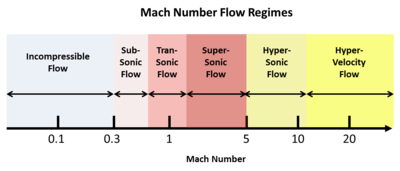
对于马赫数分类不是随便找个速度就分的，而是从实验、理论中发现，在跨越那个马赫数后，某些特性会变得相当明显。在流速非常慢时，由于音速快上许多，马赫数就变得无关紧要，数学上可将其忽略。但是，一旦流动速度接近音速，马赫数就变得非常重要，并且开始出现激波。因此，跨音速状态是通过不同的（且更为复杂的）数学来描述。在超音速状态下，流动以带有斜角的波运动为主，类似于马赫角。在大约5马赫以上时，这些波角变得很小，以至于需要使用不同的数学方法来定义超高音速状态。最后，从轨道进入行星大气层时，速度达到数公里/秒，音速现在已经相当慢，以至于在超高速状态下它在数学上又被忽略了。

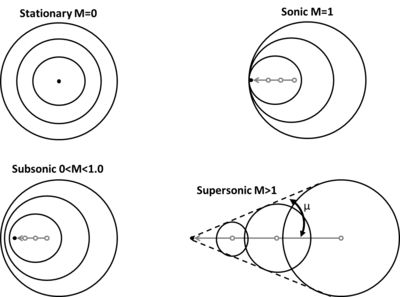
当物体在气体中从亚音速加速到超音速时，会发生不同类型的波动现象。为了说明这些变化，下图显示了一个发出对称声波的固定点(M = 0)。在均匀的流体中，声速在所有方向上都是相同的，因此这些波只是同心球体。随着发声点开始加速，声波在运动方向上“靠拢”，而在相反方向上“远离”。当该点达到音速(M = 1)时，它与其产生的声波以相同速度传播。因此，无限数量的这些声波在该点之前“堆积”，从而形成激波。在达到超音速流动后，粒子运动得如此之快，以至于它不断地将声波留在后面。发生这种情况时，这些点后面的波的轨迹会产生一个称为马赫波角或马赫角μ的角度：

$\mu =\arcsin \left({\frac {a}{V}}\right)=\arcsin \left({\frac {1}{M}}\right)$

其中$a$代表气体中声音的速度， $V$代表物体的速度。尽管这些斜波以奥地利物理学家恩斯特•马赫的名字命名，但最早是由克里斯汀多普勒发现。

波动和声速

单维流动

单维(1-D)流是指通过管道或通道的气流，假定其中的流量参数仅沿一个空间维度（即管道长度）显着变化。在分析一维通道流时，进行了许多假设：

• 管路长度与宽度之比(L/D)≤约5（以忽略摩擦和传热），
• 稳定流vs.不稳定流，
• 流动是等熵的（即可逆且绝热的过程），
• 理想气体定律（即P =ρRT）

拉伐尔喷嘴

随着流速从亚音速加速到超音速状态，气流经过喷嘴和扩散器的物理特性发生了变化。利用流体动力学和热力学的守恒定律，建立了以下与通道流动的关系（质量守恒和动量守恒相结合）：

$dP\left(1-M^{2}\right)=\rho V^{2}\left({\frac {dA}{A}}\right)$ ，

其中dP是压力的微小变化，M是马赫数，ρ是气体密度，V是流速，A是管道截面积，dA是管道面积的微小变化。从方程式中可以知道，对于亚音速流，收缩管道(dA<0)会增加流速，而扩张管道(dA>0)会降低流速。

但当气流超过音速时，因为(1- M ²)成为负值，让流动现象相反。现在，收缩管道(dA<0)会降低流速，而扩张管道(dA>0)会提高流速。在Mach = 1时，会发生特殊情况，其中管路截面积必须为最大或最小。实务上，只有让1马赫发生在管路的最小截面积，才可以在前方加速、后方继续达到更高的流速。

表中显示了随着马赫数的变化喷嘴和扩散器的物理趋势发生逆转的情况

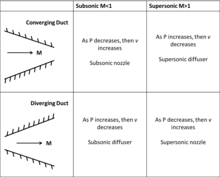
因此，为了将气流加速到1马赫，必须将喷嘴设计为收缩到最小截面积，然后扩张。在古斯塔夫·拉伐尔古斯塔夫·拉伐尔发明了这种喷嘴之后，这种类型的喷嘴（收缩喷嘴）会称为拉伐尔喷管。

当亚音速流进入收缩管道且面积减小时，气流加速。到达管道的最小面积（也称为喷喉）后，流速必须达到1马赫。如果要继续提高流速，则必须降低其密度，以遵守质量守恒原则。为了让密度降低，气流必须膨胀。

拉伐尔喷嘴

气体可达到的最大速度

最终，由于能量守恒，气体基于其能量含量会限制在某个最大速度。气体可以达到的最大速度V _max为：

$V_{\text{max}}={\sqrt {2c_{p}T_{t}}}$

其中c _p是气体的定压比热，T _t是气流停滞温度。

等熵流马赫数关系

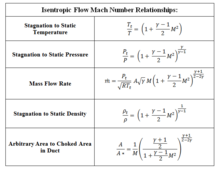
利用前述的守恒定律和热力学，建立了多种形式的关系

${\frac {{\text{property}}_{1}}{{\text{property}}_{2}}}=f(M,\gamma )$

其中M是马赫数，γ是比热之比（空气可直接假定为1.4）。

等熵流关系表。与等熵流场特性相关的方程式。

达到超音速

如先前所述，为了使气流超音速，它必须通过管路面积最小处或喷喉。此外，要达到1马赫，压力与全压的比值P _b / P _t大约为2_。一旦达到1马赫，喷喉处的流速就会阻塞。因为下游的变化只能以音速向上游移动，所以在流量阻塞后，通过喷嘴的质量流动不会受到下游条件变化的影响。

气体的非等熵单维通道流-正激波

正激波是垂直于局部流动方向的激波。

这些激波在压力波累积并聚集成极薄的激波时产生，该激波将动能转换为热能。因此，这些波会相互抵消，也可能相互增强，于是从一系列无限小声波中形成单一个激波。由于跨越激波的状态变化高度不可逆，因此激波会造成的熵大量增加。当分析正激波时，运用理想气体、单维、稳定和绝热流动等假设。停滞温度和停滞焓在激波上游和下游相同。

Rankine-Hugoniot方程，连结了正激波之前和之后的条件。

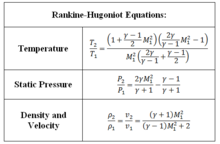
可以定点正激波或移动正激波中任何一个来轻松分析正激波。正激波之前的流动必须是超音速的，而正激波之后的流动必须是亚音速的。 Rankine-Hugoniot方程用于求解流动条件。

二维流

一维流只是二维流的一种特殊情况。因此，一维流动的定义现象之一，即正激波，同样只是斜激波中的特例。斜激波在以下应用中更为常见：飞机进气口设计、超音速飞行以及超音速喷嘴和扩散器。根据流动条件，斜激波可以以艏激波的形式附着在流体上、或从流体上脱离。

超音速风洞中X-15模型与附着的激波

钝形体的艏激波

斜激波

斜激波

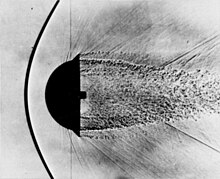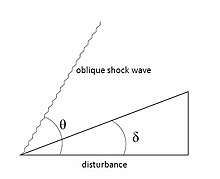
斜激波与正激波相似，但它与流动方向的夹角小于90°。当障碍物以一个不为零的角度（δ）进入流场中时，流场必须响应变化的边界条件。因此，形成斜激波，导致流动方向的改变。

激波极座标图

激波极座标图

根据流场偏转的程度（δ），斜激波又分为强或弱。强斜激波的特点是更大的角度和整个震荡的熵损失，而弱斜激波则相反。为了粗略地了解这些激波的差异，可以使用激波极座标图。激波后的静温T *，即激波后的声速定义为：

$A^{*}={\sqrt {\gamma RT^{*}}}$

其中R为气体常数，γ为比热比。马赫数可以分解为卡氏坐标

${\begin{aligned}M_{2x}^{*}&={\frac {V_{x}}{a^{*}}}\\M_{2y}^{*}&={\frac {V_{y}}{a^{*}}}\end{aligned}}$

用V _x和V _y作为流体速度V的x和y分量。借由给出激波前的马赫数，可以指定条件的轨迹。在一些δ_max从强斜激波过渡到弱斜激波。当δ= 0°时，在强斜激波的极限处会产生正激波，而在弱斜激波的极限处会产生马赫波。

斜激波反射

由于激波的倾斜，在产生斜激波后，它可以三种方式与边界相互作用，下面将对两种方式进行说明。

固体边界

首先使流场旋转角度δ，该激波从固体边界反射，并且流动由–δ转向，再次与边界平行。重要的是要注意，每个过程产生的斜激波都更加弱，并且波角会逐渐增加。

不规则反射

不规则反射与上述情况非常相似，但要注意的是δ大于最大允许转向角。因此，形成了分离的激波并且发生了更复杂的反射。

普朗特–迈耶扇

普朗特–迈耶扇可以分为压缩扇和扩张扇。 普朗特–迈耶扩张扇能够跨越边界层（即流体和固体），该边界层也以不同的变化做出反应。当激波打在固体表面时，所得扇将作为对面类型的扇返回，而当击中自由边界时，扇将作为对面类型的扇返回。

普朗特–迈耶扩张扇

普朗特–迈耶扩张扇

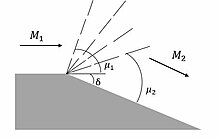
在普朗特和迈耶提出理论以前，唯一会讨论到的流体现象是激波，它会减慢流动并增加其熵。而此后，人们才知道普朗特－迈耶膨胀扇现象，是另一个造成超音速流动的可能。

与流场遇到倾斜的障碍物并形成斜激波相反，流体流经凸角扩展并透过一系列等熵马赫波形成膨胀扇。扩张“扇”由从初始马赫角到最终马赫角的马赫波组成。由于马赫数的增加仅与通道的凸角（δ）成比例，因此流体可以围绕尖角或圆角均匀扩张。产生普朗特 - 迈耶扇的扩展角可以是尖锐的（如图所示）或圆形的。如果总转向角度相同，则普朗特 - 迈耶扇之解也将相同。

普朗特 - 迈耶扩张可以看作是拉伐尔喷嘴操作的物理解释。喷嘴的轮廓产生了一系列平滑且连续的普朗特 - 迈耶扩张波。

普朗特 - 迈耶压缩扇

基本普朗特 - 迈耶压缩

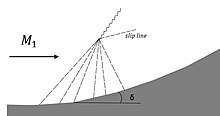
普朗特 - 迈耶压缩是与扩张相反的现象。

如果将气流逐渐转过δ角，则可以形成压缩扇。该扇也是一系列马赫波，最终会合并为斜激波。因为流场是由等熵区域（经过扇的流场）和等熵区域（通过斜激波的流场）所定义，故在两个流动区域之间会产生一条滑移线。

应用

超音速风洞

超音速风洞用于测试和研究超音速流，大约在1.2至5的马赫数范围内。风洞背后的工作原理是在上游到下游保持极大压差，从而驱动气流。

超音速风洞分类

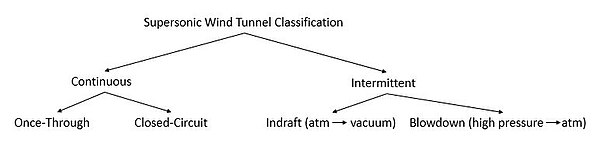
风洞可分为两类：连续运行和间歇运行的风洞。

连续运行的超音速风洞需要一个独立的电力来源，随着测试部分的尺寸越来越大，需要的电源会急剧增加。间歇性超音速风洞的价格较低，因为它们可以在很长的时间里慢慢存储电能，然后在简短的测试中一次释放。两者之间的差异就像电池和电容器。

吹放式超音速风洞示意图

兰利研究中心吸入式超音速风洞的真空球

吹放式超音速风洞具有较高的雷诺数，较小的储气罐和随时可用的干燥空气。但是它们的高压可能造成危险，导致难以保持恒定的停滞压力，并且在操作过程中会产生较大噪音。

吸入式超音速风洞与压力隐患无关，允许恒定的停滞压力，并且相对安静。不幸的是，它们的雷诺数范围有限，并且需要大型真空储存槽。

毫无疑问，知识是借由在超音速风洞中进行研究和测试而获得；然而，这些设施通常需要大量的电力，来维持测试条件所需的高压力比。例如，阿诺德工程发展中心拥有世界上最大的超音速风洞，却需要足以照明一座小城市的电力才得以运行。因此，大型风洞在大学中变得不那么普遍了。

超音速飞机进气道

斜激波最常见的需求是在超音速飞机的进气口设计，其速度大于2马赫（F-16的最大速度为2马赫，但不需要斜激波进气）。进气口的目的之一是使进入的超音速空气在进入涡轮喷气发动机之前减速至亚音速，从而最大程度地减少激波损失。这是通过以下一种或多种斜激波来完成的，最后是非常弱的正激波，上游马赫数通常小于1.4。通过进气道的气流必须在从最大音速到零，这样极大的速度范围内被正确管理。这需要改变进气道表面的位置来完成。

进气口的几何形状必须要可以变化才能应付从起飞到超过2马赫的速度，例如，对于约3马赫的最大速度， XB-70使用具有可调节斜度的矩形入口，而SR-71使用具有可调节中心锥度的圆形入口。

XB-70带有斜面的矩形进气口

SR-71带有中心体的圆形进气口

参见

• 不可压缩流
• 守恒定律
• 熵
• 状态方程
• 气体动力学
• 绝热指数
• 各向同性喷嘴流量
• 拉格朗日和欧拉流场规范
• 普朗特－迈耶函数
• 热力学，尤其是“常见的热力学过程”和“热力学定律”

参考资料

• Liepmann, Hans W.; Roshko, A. Elements of Gasdynamics. Dover Publications. 1957 [1957]. ISBN 0-486-41963-0. 
• Anderson, John D. Jr. Modern Compressible Flow 3rd. McGraw-Hill Science/Engineering/Math. 2003 [1982]. ISBN 0-07-242443-5. 
• John, James E.; Keith, T. G. Gas Dynamics 3rd. Prentice Hall. 2006 [1969]. ISBN 0-13-120668-0. 
• Oosthuizen, Patrick H.; Carscallen, W. E. Introduction to Compressible Flow 2nd. CRC Press. 2013 [1997]. ISBN 978-1439877913. 
• Zucker, Robert D.; Biblarz, O. Fundamentals of Gas Dynamics 2nd. Wiley. 2002 [1977]. ISBN 0471059676. 
• Shapiro, Ascher H. The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press Company. 1953. ISBN 978-0-471-06691-0. 
• Anderson, John D. Jr. Hypersonic and High Temperature Gas Dynamics. AIAA. 2000 [1989]. ISBN 1-56347-459-X. 

外部链接

• NASA可压缩空气动力学初学者指南
• 弗吉尼亚理工大学可压缩流量计算器 （页面存档备份，存于互联网档案馆）
• [1] （页面存档备份，存于互联网档案馆）