正三角形镶嵌
外观
(重定向自三角形鑲嵌)
 | |||
| 类别 | 正镶嵌 | ||
|---|---|---|---|
| 对偶多面体 | 正六边形镶嵌 | ||
| 识别 | |||
| 鲍尔斯缩写 | trat | ||
| 数学表示法 | |||
| 考克斯特符号 | |||
| 施莱夫利符号 | {3,6} {3[3]} | ||
| 威佐夫符号 | 6 | 3 2 3 | 3 3 | 3 3 3 | ||
| 康威表示法 | dH | ||
| 特殊面或截面 | |||
| 梵奥斯截面 | 无限边形[2] | ||
| 组成与布局 | |||
| 顶点图 | 3.3.3.3.3.3(或36) | ||
| 顶点布局 | 36 | ||
| 对称性 | |||
| 对称群 | p6m, [6,3], (*632) p3m1, [3[3]], (*333) p3, [3[3]]+, (333) | ||
| 旋转对称群 | p6, [6,3]+, (632) p3, [3[3]]+, (333) | ||
| 图像 | |||
| |||
在几何学中,正三角形镶嵌、又称为正三角方格[3]是一种正多边形在平面上的密铺,又称正镶嵌图。
命名
[编辑]康威称正三角形镶嵌为deltille。deltille一词来自于外形为三角形的希腊字母 Delta (Δ),有时也称作六角化正六边形镶嵌。
性质
[编辑]由于正三角形镶嵌是由正三角形组成,又因正三角形内角为60度,因此每个顶点周围都有6个三角形,且刚好占满360度。
正三角形镶嵌在施莱夫利符号中,用{3,6}表示。
正三角形镶嵌是三个的平面正镶嵌图之一。另外两个是正方形镶嵌和正六边形镶嵌。
一般将画在纸上的正三角方格称作正三角格纸[3],正三角格纸是用来画三维立体图或三维透视图用的。使用正三角格纸作图会比较容易做出三维立体图或三维透视图,而且图形看起来比较接近三维[3]。
上色的正三角形镶嵌
[编辑]正三角形镶嵌有九种不同的上色方式,他们依顶点周为颜色数来命名: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314。
| 上色 索引 |
111111 | 121212 | 121314 | 121213 |
|---|---|---|---|---|
| 图示 | ||||
| 上色 | 
|

|

|

|
| 对称群 | *632 (p6m) [6,3] |
*333 (p3m1) [3[3]] = [1+,6,3] |
333 (p3) [3[3]]+ |
3*3 (p31m) [6,3+] |
| Wythoff符号 | 6 | 3 2 | 3 | 3 3 | | 3 3 3 | |
| 考克斯特符号 |
A2晶格和圆堆砌
[编辑]正三角形镶嵌的顶点排布被称作A2晶格[4]。正三角形镶嵌是单纯形堆砌家族的二维成员。
A2*晶格(又称A23),可由所有3种A2晶格组合得来,就等价于A2晶格。


 +
+ 

 +
+ 

 =
= 

 的对偶 =
的对偶 = 


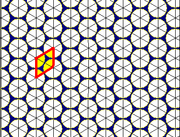
以正三角形镶嵌的顶点为圆心,我们可以得到二维的最密圆堆砌,每个圆都与6个相邻圆接触(接触数),堆砌密度为或90.69%。由于3个A2晶格组合还是A2晶格,这种圆堆砌种的圆可被涂成三种颜色。
A2晶格的沃罗诺伊图是正六边形镶嵌,它也是正三角形镶嵌的对偶。因此,正六边形镶嵌也与最密圆堆砌有直接的对应关系。
| A2晶格圆堆砌 | A* 2晶格圆堆砌 |
|---|---|
|

|
| 正六边形镶嵌 | |

|

|
相关半正镶嵌
[编辑]| 对称性: [6,3], (*632) | [6,3]+, (632) | [1+,6,3], (*333) | [6,3+], (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
||
| {6,3} | t0,1{6,3} | t1{6,3} | t1,2{6,3} | t2{6,3} | t0,2{6,3} | t0,1,2{6,3} | s{6,3} | h{6,3} | h1,2{6,3} | |
| 半正对偶 | ||||||||||

|

|

|

|

|

|

|

|

| ||
| V6.6.6 | V3.12.12 | V3.6.3.6 | V6.6.6 | V3.3.3.3.3.3 | V3.4.12.4 | V.4.6.12 | V3.3.3.3.6 | V3.3.3.3.3.3 | ||
从六边形镶嵌可利用“交错”操作将六边形镶嵌变成三角形镶嵌。
| 球面镶嵌 | 多面体 | 欧式镶嵌 | 紧凑双曲镶嵌 | 仿紧空间 | 非紧空间 | ||||
|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | ∞ | ||
| 2n边形镶嵌 | {2,3} | {4,3} | {6,3} | {8,3} | {10,3} | {12,3} | {∞,3} | {iπ/λ,3} | |
| 交错2n边形镶嵌 |  h{2,3} |
 h{4,3} |
 h{6,3} |
 h{8,3} |
 h{10,3} |
 h{12,3} |
... |  h{∞,3} |
 h{iπ/λ,3} |
相关
[编辑]参考文献
[编辑]- ^ Coxeter, H.S.M., Regular Complex Polytopes, Cambridge University Press, 1991, ISBN 0-521-39490-2
- ^ Coxeter, Complex Regular polytopes,[1] p.141
- ^ 3.0 3.1 3.2 《图解数学辞典》天下远见出版 P.50 ISBN 986-417-614-5
- ^ 存档副本. [2014-01-26]. (原始内容存档于2021-02-25).
阅读
[编辑]- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- Grünbaum, Branko ; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- 埃里克·韦斯坦因. Triangular Grid. MathWorld.
- Klitzing, Richard. 2D Euclidean tilings x3o6o - trat - O2. bendwavy.org.
- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. p35
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
- Tilings and Patterns, from list of 107 isohedral tilings, p.473-481




