圖書館:地球自转


地球自{{zy|轉|zhuàn|ㄓㄨㄢˋ}}是固體地球繞著自己的軸轉動,方向是由西向東;所以地球是由西至東自轉的。從天球的北極點鳥瞰,地球自轉是逆時針方向旋轉;從南極點上空看是順時針方向旋轉。
自轉的周期
[編輯]真正週期
[編輯]地球自轉的周期是一個恆星日,目前其值為23時56分4秒。但是近年來地球自轉周期在緩慢增加(即轉速緩慢減小),導致需要對全球計時器進行調整,例如2005年12月31日全球鐘錶統一加一秒。這樣的調整稱為閏秒。
轉動速度
[編輯]地球自轉的角速度大約是每小時15度;而表面每點的線速度隨緯度而變化,是赤道的線速度乘以緯度的餘弦。因此赤道的線速度是最大的,兩極的線速度最小,而赤道線的速度約465.1 m/s。
恆星日與太陽日
[編輯]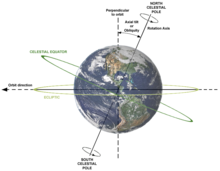
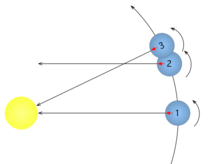
地球相對於太陽的轉動一週的時間(從正午至正午)稱為真太陽日或視太陽日,由於地球橢圓軌道的離心率和自轉軸的傾斜,導致均時差的形成。這兩者都以數千年的尺度變化[1],所以真太陽日也有周年性的變化。通常,每年有兩段時期比平均太陽日長,另外兩段時期比平均太陽日短{{#tag:ref|When Earth's eccentricity exceeds 0.047 and perihelion is at an appropriate equinox or solstice, only one period with one peak balances another period that has two peaks.[2]|group=n}}。當真太陽日在越接近近日點時越長,這是因為這時的太陽看起來在黃道上移動的角度比平常大,朝向近日點接近時,每一天增長的時間大約在{{nowrap|10秒鐘}};反過來,當地球朝向遠日點接近時,每一天的時間大約會縮短約{{nowrap|10秒鐘}}。當接近至點時,太陽的視運動從黃道上投影至天球赤道上的移動量會增加,導致每一天可以增長約{{nowrap|20秒鐘}};但反過來,在接近分點時,天球赤道和黃道幾乎重合,因此沒有甚麼差別。通常,近日點和至點的效果結合,在接近{{nowrap|12月22日}}時,真太陽日每一天可以增長{{nowrap|30秒鐘}};但是至點的效應在遠日點時會被抵銷一部分,所以約在{{nowrap|6月19日}},只會增長{{nowrap|13秒鐘}}。相對來說,分點的效應,在{{nowrap|3月26日}}(接近春分)大約比平太陽日短{{nowrap|18秒鐘}},在{{nowrap|9月16日}}(接近秋分)大約短{{nowrap|21秒鐘}}[2][3][4]。
在一年中的真太陽日的平均長度稱為平太陽日,它包含了{{nowrap|86,400平}}太陽秒。目前,平太陽秒比SI的秒稍稍長了一點點,這是因為地球的平太陽日由於潮汐摩擦已經比在19世紀定義當時長了一些。在1750年至1892年之間的平太陽秒是西蒙·紐康於1895年在製作他的太陽表時制定的獨立時間單位。這個表在1900年至1983年被用來計算世界的天體曆,所以這種秒也稱為曆書秒。SI秒在1967年與曆書秒是相等的[5]。
地球相對於恆星轉動一週(360度)稱為恆星日,並依據國際地球自轉服務(IERS)的定義是{{nowrap|86,164.098 903 691}}秒的平太陽時(UT1,等於{{nowrap|23{{smallsup|h}} 56{{smallsup|m}} 4.098 903 691{{smallsup|s}}}},或{{nowrap|0.997 269 663 237 16}}平太陽日)[6]{{#tag:ref|Aoki, the ultimate source of these figures, uses the term "seconds of UT1" instead of "seconds of mean solar time".[7]|group=n}}。地球相對於歲差或平春分點的轉動週期,常被誤稱為恆星日[n 1],是{{nowrap|86,164.090 530 832 88}}秒的平太陽時(UT1,等於{{nowrap|23{{smallsup|h}} 56{{smallsup|m}} 4.090 530 832 88{{smallsup|s}}}},{{nowrap|0.997 269 566 329 08}} 平均太陽日)[6],因此天文學上用的恆星日比真實的恆星日短了大約{{nowrap|8.4 ms}}[8]。
無論是真實的恆星日或是天文學上用的恆星日都比平太陽日短了大約{{nowrap|3分}} {{nowrap|56秒}},平太陽日在SI是運用IERS從{{nowrap|1623–2005}}[9]和{{nowrap|1962–2005}}的週期[10]。

最近(1999年–2010年) 平太陽日的長度是86,400SI秒,變化率在{{nowrap|0.25 ms}}和{{nowrap|1 ms}},必須將這些變化也添加在真實的恆星日和天文的恆星日的長度,以SI秒呈現它們的平太陽時。
地球在慣性空間中的轉動速率是每SI秒{{nowrap|(7.2921150 ± 0.0000001){{E|−5}}}}弧度[6]乘上(180°/π弧度)×(86,400秒/平太陽日),得到每平太陽日360.9856°,表明了在一個太陽日的地球轉動超過相對於恆星的360°。這是因為地球在接近圓形的繞日軌道上的運動,使得地球必須在轉到對向恆星之後還得再多轉一點才能再度對向平太陽,使平太陽再度出現在同一個地點的同一方向上,即使相對於平太陽只是旋轉了一圈(360°)[n 2]。將地球每秒在赤道上旋轉的弧度乘上地球的半徑{{nowrap|6,378,137 m}}(WGS84橢球,2π弧度的因素在兩個項目中都被刪除)得到的速度是{{nowrap|465.1 m/s}}、{{nowrap|1,674.4 km/h}}或{{nowrap|1,040.4 mi/h}}[11]。有些資料來源指出地球的赤道速度較低,或是只有{{nowrap|1,669.8 km/h}}[12],這是以地球的赤道週長除以約{{nowrap|24小時}}獲得的結果。但是,這是不自覺的認為我們是在慣性空間中旋轉了一圈的時間,因此旋轉一圈的較精確時間應該是恆星日。經由乘上平太陽日對恆星日的比值,{{nowrap|1.002 737 909 350 795}},可以驗證這一點[6],因為這會獲得前述赤道在平太陽時的速度{{nowrap|1,674.4 km/h}}。
對地球自轉的長期監測需要甚長基線干涉儀的座標配合全球定位系統、衛星雷射測距和其它衛星技術配合著使用。這些提供了對世界時、進動和章動等的絕對參考[13]。
過去的數百萬年,地球的旋轉受到月球引力的交互作用影響減緩了許多:參見潮汐加速。但是有些大型的事件,像是2004年印度洋地震,就使地球的轉動加速了大約3微秒[14]。在冰河期後期的後冰河期反彈,是因為地球質量的分布改變影響了地球的慣量,經由角動量守恆,改變了轉動速率[15]。
地軸的變動
[編輯]地球的旋轉像一個陀螺,軸的指向有在恆星空間中維持一定方向的性質。來自太陽、月球和其它行星的外來力量導致這固定的方向有所偏移。地球轉軸大型、週期性的變動稱為歲差,而較小的變動稱為章動和極移。
歲差
[編輯]{{main|分點歲差}} 歲差({{lang|en|precession}})是地球的自轉軸相對於恆星空間的進動。分點的位置,相對於在天球上固定不動的恆星,沿著黃道每年向西移動。通常,每年的移動量是50.29",即每71.6年移動1°。這個過程雖然緩慢但會逐年累加起來,完整的歲差圈要經歷25,765年(稱為柏拉圖年),分點在黃道上退行一周360°。
章動
[編輯]{{main|章動}} 章動(nutation)是在行星或陀螺儀的自轉運動中,軸在進動中的一種輕微不規則運動,使自轉軸在方向的改變中出現如「點頭」般的搖晃現象。 地球的章動來自於潮汐力所引起的進動,並使得歲差的速度不是常數,而會隨著時間改變。
極移
[編輯]{{main|極移}} 極移是地球的自轉軸在地球表面橫越的運動,這是將地球視為在一個固定不變的參考座標系(所謂的地球中心、地心地固坐標系(ECEF))下所做的測量,這種變動只有幾米。
極移的原因主要有兩種,一種是地軸對於慣性軸偏離的結果,周期大約為14個月。另一種是大氣季節性運行導致,其周期為一年。還有其他一些次要的原因,極移的振幅一般不超過15米。
影響地球自轉速度的因素
[編輯]地球自轉速度主要受三個因素影響,總體使其趨慢。
- 潮汐加速:日月對海洋的引潮力使地球自轉速度變慢,令地球一日的長度每100年增加1.6毫秒,導致一年的日數減少,有證據{{來源請求}}表明泥盆紀中期的一年有400日。
- 季節變化:有周年變化和半年變化。周年變化是風的季節變化引起的,其振幅為20-25毫秒;半年變化是由日月引潮力對大氣的潮汐作用引起,其振幅約為9毫秒。
- 不規則變化:地外和地內的物質或能量交換。如隕星體對地球的撞擊等,時而使地球加速時而使地球變慢,而地震往往使地球加速自轉。
地球自轉的規律性
[編輯]規律性
[編輯]地軸的進動是一種圓錐形的運動,其規律性如下:
表現
[編輯]原因
[編輯]第一,地球形狀
因為地球是一個明顯的扁球體,所以隆起的部位所受的附加引力總是稍大於另一側。二者之間的差值,總是存在於接近日月的一側。
第二,黃赤交角
由於黃赤交角的存在,使得日月經常在赤道面以外對赤道隆起施加引力。這樣上述引力差就成為一個力矩,使得地軸趨近黃軸,天極趨近黃極。
第三,地球自轉
因為上述的引力差,給地球的自轉的角動量增加了一個增量,使得地球的自轉方向發生偏轉。這就是地軸的進動,也就是歲差。
起源
[編輯]
在理論上,地球的形成是太陽系誕生的一部分:最初只是大量的、旋轉中的塵埃、岩石和氣體,最後終於形成太陽系。組成它的化學元素是來自大爆炸產生的氫和氦,還有超新星釋放出的重元素。這個星際塵埃是不均勻的,重力吸積過程上任何的不對稱,導致最終形成行星的角動量[16]。 目前的轉動週期是初始的旋轉受到其它因素影響的結果,包括潮汐力和忒伊亞碰撞假說。
地球自轉的證據
[編輯]在地球轉動的參考座標系中,一個自由運動物體的路徑,相對於一個固定參考座標系統,會產生視路徑偏移的現象。由於受到科氏力的影響,下落的物體將會從垂直於釋放點的鉛錘線上向東偏移,並且在北半球的彈道會從它們射出的方向向右偏轉(南半球的向左偏轉)。科氏力的影響有各種不同的表現形式,特別是在氣象現象上,南半球和北半球的氣旋有著不同的旋轉方向。虎克,依據牛頓在1679年的建議,從{{nowrap|8.2米}}的高度拋下一顆球,預測會向東偏移半毫米,但是這個實驗未能成功。而最終在18世紀末和19世紀初才由波洛尼亞的Giovanni Battista Guglielmini、漢堡的Johann Friedrich Benzenberg,和弗萊貝格的Ferdinand Reich,使用高塔小心的釋放質量才獲得結果[n 3]。
傅科擺
[編輯]證明地球自轉最著名的證據是傅科擺,它是物理學家萊昂·傅科在1851年首度建造的,他在法國巴黎的先賢祠從塔頂懸掛了一個擺長{{nowrap|67 m}}的鐵球。由於地球的自轉使得擺的擺動平面產生搖擺的振盪,而旋轉的速度取決於緯度。在巴黎的緯度,預測和觀測到的偏移是每小時大約順時針的偏轉{{nowrap|11度}}。現在,世界各地許多的博物館都有傅科擺的設置。
相關條目
[編輯]註解
[編輯]- ^ Sidereal day is arguably a misnomer because the dictionary definition of sidereal is "relating to the stars", thus fostering confusion with the stellar day.
- ^ In astronomy, unlike geometry, 360° means returning to the same point in some cyclical time scale, either one mean solar day or one sidereal day for rotation on Earth's axis, or one sidereal year or one mean tropical year or even one mean Julian year containing exactly {{nowrap|365.25 days}} for revolution around the Sun.
- ^ See {{link-de|Fallexperimente zum Nachweis der Erdrotation|Fallexperimente zum Nachweis der Erdrotation}}(German Wikipedia article).
參考資料
[編輯]{{reflist}}
外部連結
[編輯]- Earth Orientation Center: Earth rotation data and interactive analysis){{Wayback|url=http://hpiers.obspm.fr/eop-pc/ |date=20110302164002 }}
- Reason for Earth's rotation
- Why is the earth rotating ?{{Wayback|url=http://ivarun.blogspot.com/2007/07/who-pushed-earth-in-past.html |date=20100119001023 }}
- Weather Makes Earth Wobble{{Wayback|url=http://www.livescience.com/forcesofnature/060626_earth_wobbles.html |date=20080518053335 }}
- Earth rotation by Jean O. Dickey{{Wayback|url=http://www.agu.org/reference/gephys/24_dickey.pdf |date=20090305185438 }}
- International Earth Rotation and Reference Systems Service (IERS){{Wayback|url=http://www.iers.org/ |date=20220920025430 }}
- AAM Scientific Background Information(1.36 MB pdf file)
- Historical Eclipses and Earth’s rotation by F. Richard Stephenson(242KB pdf file)
- Spinning earth animation
- ^ {{Cite web |url=http://mb-soft.com/public3/equatime.html |title=Derivation of the equation of time |accessdate=2010-10-08 |archive-date=2010-09-24 |archive-url=https://web.archive.org/web/20100924234324/http://mb-soft.com/public3/equatime.html |dead-url=no }}
- ^ 2.0 2.1 Jean Meeus, Mathematical astronomy morsels (Richmond, Virginia: Willmann-Bell, 1997) 345–6.
- ^ {{Cite web |url=http://www.jgiesen.de/planets/img/EoTGraph.gif |title=Equation of time in red and true solar day in blue |accessdate=2010-10-08 |archive-date=2010-10-09 |archive-url=https://web.archive.org/web/20101009232844/http://jgiesen.de/planets/img/EoTGraph.gif |dead-url=no }}
- ^ {{Cite web |url=http://www.pierpaoloricci.it/dati/giornosolarevero_eng.htm |title=The duration of the true solar day |accessdate=2010-10-08 |archive-date=2009-08-26 |archive-url=https://web.archive.org/web/20090826184737/http://www.pierpaoloricci.it/dati/giornosolarevero_eng.htm |dead-url=yes }}
- ^ {{Cite web |url=http://tycho.usno.navy.mil/leapsec.html |title=Leap seconds by USNO |accessdate=2010-10-09 |archive-date=2012-05-27 |archive-url=https://www.webcitation.org/67yIZgtef?url=http://tycho.usno.navy.mil/leapsec.html |dead-url=no }}
- ^ 6.0 6.1 6.2 6.3 {{Cite web |url=http://hpiers.obspm.fr/eop-pc/models/constants.html |title=IERS EOP Useful constants |accessdate=2010-10-09 |archive-date=2012-11-03 |archive-url=https://www.webcitation.org/6Bto7IZMb?url=http://hpiers.obspm.fr/eop-pc/models/constants.html |dead-url=yes }}
- ^ Aoki, et al., "The new definition of Universal Time {{Wayback|url=http://adsabs.harvard.edu/abs/1982A%26A...105..359A |date=20190403115447 }}", Astronomy and Astrophysics 105 (1982) 359–361.
- ^ Explanatory Supplement to the Astronomical Almanac, ed. P. Kenneth Seidelmann, Mill Valley, Cal., University Science Books, 1992, p.48, ISBN 0-935702-68-7.
- ^ IERS Excess of the duration of the day to 86,400s…since 1623 {{Wayback|url=http://hpiers.obspm.fr/eop-pc/earthor/ut1lod/lod-1623.html |date=20081003083543 }} Graph at end.
- ^ {{Cite web |url=http://hpiers.obspm.fr/eop-pc/earthor/ut1lod/figure3.html |title=IERS Variations in the duration of the day 1962–2005 |accessdate=2007-08-13 |archive-date=2007-08-13 |archive-url=https://web.archive.org/web/20070813203913/http://hpiers.obspm.fr/eop-pc/earthor/ut1lod/figure3.html |dead-url=no }}
- ^ Arthur N. Cox, ed., Allen's Astrophysical Quantities {{Wayback|url=http://books.google.com/books?id=w8PK2XFLLH8C&pg=PA244 |date=20130214082827 }} p.244.
- ^ Michael E. Bakich, The Cambridge planetary handbook {{Wayback|url=http://books.google.com/books?id=PE99nOKjbXAC&pg=PA50 |date=20130214082830 }}, p.50.
- ^ {{Cite web |url=http://hpiers.obspm.fr/eop-pc/techniques/techniques.html |title=Permanent monitoring |accessdate=2010-10-11 |archive-date=2010-11-15 |archive-url=https://web.archive.org/web/20101115150919/http://hpiers.obspm.fr/eop-pc/techniques/techniques.html |dead-url=no }}
- ^ Sumatran earthquake sped up Earth's rotation {{Wayback|url=http://www.nature.com/news/2004/041229/full/news041229-6.html |date=20110203013149 }}, Nature, December 30, 2004.
- ^ {{cite journal |last=Wu |first=P. |coauthors=W.R.Peltier |year=1984 |title=Pleistocene deglaciation and the earth's rotation: a new analysis |url=https://archive.org/details/sim_geophysical-journal-of-the-royal-astronomical-society_1984-03_76_3/page/753 |journal=Geophysical Journal of the Royal Astronomical Society |volume=76 |pages=753–792}}
- ^ {{cite web |url = http://curious.astro.cornell.edu/question.php?number=416 |title = Why do planets rotate? |work = Ask an Astronomer |deadurl = yes |archiveurl = https://web.archive.org/web/20070609093745/http://curious.astro.cornell.edu/question.php?number=416 |archivedate = 2007-06-09 |accessdate = 2010-10-08 }}
